「学习笔记」Treap

前言

HuaQiMoAo 大佬

GuoShaoYang 大佬

且部分图片可能来源于这两位大佬。 本人太菜，不会画图

接下来开始我们的恶心数据结构旅程吧…首先送大家两句话：

• 智力不够，数据结构来凑。
• 如果数据结构题你一遍码不对，那就直接删了重码吧，反正你也调不出来。

这两句话一定要牢记，一定啊，一定啊…

什么是 Treap ?

什么是 $Treap$ ?

这是一个新学者的再普通不过的疑问。

下面给出一个定义：

Treap 是一种平衡树。这个单词的构造选取了 Tree (树)的前两个字符和Heap(堆)的后三个字符，Treap = Tree + Heap。顾名思义，Treap 把 BST 和 Heap 结合了起来。它和 BST 一样满足许多优美的性质，而引入堆目的就是为了维护平衡。

Treap 在 BST 的基础上，添加了一个修正值。在满足 BST 性质的基础上，Treap 节点的修正值还满足最小堆性质 。最小堆性质可以被描述为每个子树根节点都小于等于其子节点。

这个定义，其实看不懂是最正常的 大佬请直接忽略不计

这个定义里面给出了几个新概念：

• 平衡树（这个可以不用说明吧…）
• 树 $Tree$ （这个也不用说明吧…）
• 堆 $Heap$ 以及最小堆
• 二叉搜索树 $BST$

我们分别对这些概念进行解释。

---

二叉搜索树 (Binary Search Tree/Binary Sort Tree/BST)

这看上去是一个很高档的名字。

但是其思路却和我们普遍见到的二分查找是一样的，它只不过是将二分搜索的过程换到树上实现，并且支持插入而已。

这里给出其定义：

二叉查找树(Binary Search Tree)是基于插入思想的一种在线的排序数据结构。它又叫二叉搜索树(Binary Search Tree)、二叉排序树(Binary Sort Tree)，简称 BST。

这种数据结构的基本思想是在二叉树的基础上，规定一定的顺序，使数据可以有序地存储。二叉查找树运用了像二分查找一样的查找方式，并且基于链式结构存储，从而实现了高效的查找效率和完美的插入时间。

那么这种特殊的树有什么特性呢？

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉查找树。

简而言之，二分查找是怎么实现的，他就有哪些实现时特判过的特性。

清楚这些之后，代码实现也不难。

---

基础定义

BST 代码中任意节点的定义

#define MAXN 500000
struct node{
	int key; //键值
	node *ch[2]; //左右儿子指针
};
node tree[MAXN+5]; //存结点的数组，集中申请，逐个分配
node *root, *NIL, *ncnt; //根结点指针、伪空指针、结点分配计数器指针

BST 的初始化

void Init(){
	NIL=&tree[0];
	NIL->ch[0] = NIL->ch[1] = NIL; //形成闭环
	ncnt=&tree[1];
	Root=NIL;
}

BST 中生成新节点

inline node *NewNode(int val){
    node *p=++ncnt;
    p->key=val;
    p->ch[0]=p->ch[1]=NIL;
    return p;
}

---

处理完 $BST$ 的基础代码，现在来看一下它的一些更高级的操作：

查找元素

首先分析一下我们查找元素的过程（此处可结合二分搜索的思路）

对于一个已知的二叉查找树，在其中查找特定的值。

1. 从根节点开始查找
2. 如果当前节点的值就是要查找的值，查找成功
3. 如果要查找的值小于当前节点的值，在当前节点的左子树中查找该值
4. 如果要查找的值大于当前节点的值，在当前节点的右子树中查找该值
5. 如果当前节点为空节点，查找失败，二叉查找树中没有要查找的值

通过返回结点是否为NIL，可以判断查找是否成功。查找的期望时间复杂度为 $O(logN)$ 。

以下是代码实现：

node * Find(node *rt, int val){
	if(rt == NIL){return NIL;}
	if(rt->key == val) return rt;
	int d = (val >= rt->key);
	return Find(rt->ch[d], val);
}

可见，其实 $BST$ 和二分查找没什么区别…

---

插入元素

在二叉查找树中插入元素，要建立在查找的基础上。基本方法是类似于线性表中的二分查找，不断地在树中缩小范围定位，最终找到一个合适的位置插入。

具体方法如下所述。

1. 从根节点开始插入

2. 如果要插入的值小于等于当前节点的值，在当前节点的左子树中插入

3. 如果要插入的值大于当前节点的值，在当前节点的右子树中插入

4. 如果当前节点为空节点，在此建立新的节点，该节点的值为要插入的值，左右子树为空，插入成功。

对于相同的元素，一种方法我们规定把它插入左边或者右边，另一种方法是我们在节点上再加一个域cnt，记录重复节点的个数。

插入的期望时间复杂度为 $O(logN)$ 。

代码实现：

void Insert(node * &rt, int val){
	if(rt == NIL){
        rt = NewNode(val);
        return ;
	}
	int d = (val >= rt->key); //相同的元素作为单独的结点插到右子树
	Insert(rt->ch[d], val);
}

---

删除元素

有了插入就有删除…二叉查找树的删除稍有些复杂，要分三种情况分别讨论。

基本方法是要先在二叉查找树中找到要删除的结点的位置，然后根据结点分以下情况：

• 情况一，该节点是叶节点(没有非空子节点的节点)，直接把节点删除即可。

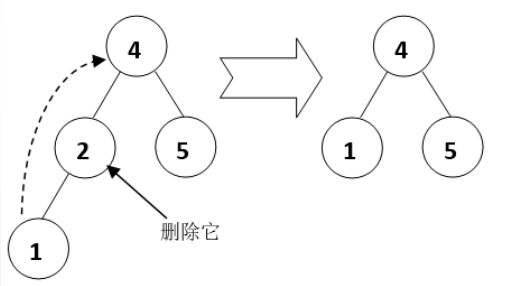
• 情况二，该节点是链节点(只有一个非空子节点的节点)，为了删除这个节点而不影响它的子树，需要把它的子节点代替它的位置，然后把它删除。如图所示，删除节点2时，需要把它的左子节点代替它的位置。

  

• 情况三，该节点有两个非空子节点。由于情况比较复杂，一般的策略是用它右子树的最小值来代替它，然后把它删除。如图所示，删除节点2时，在它的右子树中找到最小的节点3，该节点一定为待删除节点的后继。删除节点3(它可能是叶节点或者链节点)，然后把节点2的值改为3。也可以使用它的前驱(左子树的最大值)代替它本身。操作方法相同。也可以使用它的前驱(左子树的最大值)代替它本身。操作方法相同。为了方便查找后继结点，在每个结点上新增了父指针fa，这样构建的二叉树是双向链表。插入结点时在维护向下的指针时，也要同步维护向上的指针。
  
  代码实现

void Delete(node *rt, int val) { //z:要删除的结点, y:操作中删除的结点，可能是z，也可能是z的后继
    node *x, *y, *z = Find(rt, val);
    if(z == NIL) return;
    if(z->ch[0] == NIL || z->ch[1] == NIL) y = z; //情况1，2
    else y = FindNext(z); //情况3
    if (y->ch[0] != NIL) x = y->ch[0]; // x: y的左子或右子
    else x = y->ch[1];
    if(x != NIL) x->fa = y->fa;
    if(y->fa == NIL)Root = x;
    else if(y == y->fa->ch[0])y->fa->ch[0] = x;
    else y->fa->ch[1] = x;
    if(y != z)z->key = y->key;
}

同时，我们也可以改进一下 $insert$ 操作

node * FindNext(node *rt) {
	if(rt == NIL) return NIL;
    node * y = rt->ch[1];
    while(y->ch[0] != NIL)y = y->ch[0];
	return y;
}
//后继结点是值键值大于当前结点的第一个结点。这里约定二叉查找树中结点的键值都不相同。

---

查找后继

其实可以直接上代码…

node * FindNext(node *rt) {
    if(rt == NIL) return NIL;
    node * y = rt->ch[1];
    while(y->ch[0] != NIL)y = y->ch[0];
    return y;
}
//后继结点是值键值大于当前结点的第一个结点。这里约定二叉查找树中结点的键值都不相同。

---

平衡性问题讨论

随机的进行 $N^2(N>=1000)$ 次插入和删除之后，二叉查找树会趋向于向左偏沉。

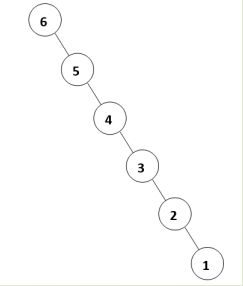
为什么会出现这种情况，原因在于删除时，我们总是选择将待删除节点的后继代替它本身。这样就会造成总是右边的节点数目减少，以至于树向左偏沉。 已经被证明，随机插入或删除 $N^2$ 次以后，树的期望深度为 $\Theta (N\frac{1}{2})$ 。对待随机的数据二叉查找树已经做得很不错了，但是如果有像这样 $6,5,4,3,2,1$ 有序的数据插入树中时，会有什么后果出现？

如图所示。二叉查找树退化成为了一条链。这个时候，无论是查找、插入还是删除，都退化成了 $O(N)$ 的时间。我们需要使二叉查找树变得尽量平衡，才能保证各种操作在 $O(logN)$ 的期望时间内完成，于是各种**自动平衡二叉查找树(Self-Balancing Binary Search Tree)**因而诞生。

---

经典例题

Aizu ALDS1_8_A Binary Search Tree I

Aizu ALDS1_8_B Binary Search Tree II

Aizu ALDS1_8_C Binary Search Tree III

---

堆 (Heap)

在 $BST$ 中，我们遗留了一个关于其平衡性的问题，而**堆 (Heap)**正好可以解决平衡性系列的问题。

为什么？给出定义即知：

堆，是一种保证任意节点的左右儿子都比自身小的完全二叉树，其深度始终保持在 $logN$ 的数量级

此数据结构运用较多（比如 $STL$ 库中的 priority_queue 即优先队列，就是小根堆），就不给出代码了。

查询操作

堆的根部即为最值，直接调取即可。

插入操作

以下内容引用自 GuoShaoYang 大佬

我们将新节点 $20$ 插入二叉树底端。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YtcCDgyd-1574688971635)(https://i.loli.net/2019/11/25/kvwnCQ17H4G9Xbr.png)]

然后不断让新节点往上跳，直到它小于它的父亲或者自己为根。

但是这还不满足堆的特征，还需要继续往上面跳。

然后，我们就完成了我们的插入操作。

删除操作

以下内容引用自 GuoShaoYang 大佬

我们用二叉树底端的节点覆盖根，然后让新的根与左右儿子比较，用较大的儿子替换根，如此往复即可。

假设我们删除上面中插入的 $20$ 。

替换掉 $20$ 。

然后执行节点跳跃操作，使其满足堆的特性

---

随机二叉查找树 (Treap)

做了很久铺垫，现在终于可以进入正题。

我们重新引用一遍定义：

Treap是一种平衡树。这个单词的构造选取了Tree(树)的前
两个字符和Heap(堆)的后三个字符，Treap = Tree + Heap。顾名思义，Treap
把BST和Heap结合了起来。它和BST一样满足许多优美的性质，而引入堆目的就
是为了维护平衡。
Treap在BST的基础上，添加了一个修正值。在满足BST性质的基础上，Treap节点的修正值还满足最小堆性质。
最小堆性质可以被描述为每个子树根节点都小于等于其子节点。

现在感觉看这个定义是否好些了？

总的来说， $Treap$ 就是集 $BST$ 与 $Heap$ 的特性于一体的一种特殊的数据结构。

现在来看一下他的一些特性：

• Treap可以定义为有以下性质的二叉树：
  1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值，而且它
     的根节点的修正值小于等于左子树根节点的修正值
  2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值，而且它
     的根节点的修正值小于等于右子树根节点的修正值
  3. 它的左、右子树也分别为Treap
• 修正值是节点在插入到Treap中时随机生成的一个值，它与节点的值无关。

基础定义

知道特性之后，我们也可以写出其定义的代码

struct treap{
    int son[2],siz,key,cnt,rd;
    //左右儿子, 树的大小, 键, 当前节点出现多少次, 随机数 (修正值)
    treap(){siz=cnt=0;}
}tre[MAXN+5];

Treap 维护平衡的原理——旋转操作

我们发现， $BST$ 会遇到不平衡的原因是因为有序的数据会使查找的路径退化成链，而随机的数据使 $BST$ 退化的概率是非常小的。在 $Treap$ 中，修正值的引入恰恰是使树的结构不仅仅取决于节点的值，还取决于修正值的值。

然而修正值的值是随机生成的，出现有序的随机序列是小概率事件，所以 $Treap$ 的结构是趋向于随机平衡的。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dCfZ9U53-1574688971646)(https://i.loli.net/2019/11/25/f7kgXuvAmbqjcHZ.png)]

那么，我们如何构建 $Treap$ ？

为了使Treap中的节点同时满足BST性质和小根堆性质，不可避免地要对其结构进行调整，调整方式被称为旋转(Rotate)。

在维护Treap的过程中，只有两种旋转 ，分别是左旋转(简称左旋)和右旋转(简称右旋)。

旋转是相对于子树而言的，左旋和右旋的命名体现了旋转的一条性质：

旋转的性质1：左旋一个子树，会把它的根节点旋转到根的左子树位置，同时根节点的右子节点成为子树的根；右旋一个子树，会把它的根节点旋转到根的右子树位置，同时根节点的左子节点成为子树的根。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fA7VF8mn-1574688971648)(https://i.loli.net/2019/11/25/xfSWXzvYeuVAIcs.png)]

如图所示，我们可以从图中清晰地看出，左旋后的根节点降到了左子树，右旋后根节点降到了右子树，而且仍然满足BST性质，于是有：

对子树旋转后，子树仍然满足 $BST$ 性质。

利用旋转的两条重要性质，我们可以来改变树的结构，实际上我们恰恰是通过旋转，使Treap节点之间满足堆序。

这里用一个例子来更清晰地说明：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RhCH9SuO-1574688971650)(https://i.loli.net/2019/11/25/hi9Y3BUP6ny5TZ8.png)]

如图所示的左边的一个Treap，它仍然满足BST性质。

但是由于某些原因，节点4和节点2之间不满足最小堆序，4作为2的父节点，它的修正值大于左子节点的修正值。

我们只有将2变成4的父节点，才能维护堆序。

根据旋转的性质我们可以知道，由于2是4的左子节点，为了使2成为4的父节点，我们需要把以4为根的子树右旋。右旋后，2成为了4的父节点，满足堆序。

为了简化代码，我们宏定义：

#define ch(i,d) tre[i].son[d]

旋转的代码：

inline void rotate(int& x,const int d){//方向 d 的儿子上来
    int i=ch(x,d);
    ch(x,d)=ch(i,d^1);
    ch(i,d^1)=x;
    pushup(x),pushup(i);
    //注：不用 pushup(ch(x,d^1)) 是因为这棵被提起来的子树并没有参与修改, 因而不用修改
    return (void)(x=i);//因为旋转，当前的点被更改
}

---

插入操作

在Treap中插入元素，与在BST中插入方法相似。

首先找到合适的插入位置，然后建立新的节点，存储元素。

但是要注意建立新的节点的过程中，会随机地生成一个修正值，这个值可能会破坏堆序，因此我们要根据需要进行恰当的旋转。具体方法如下：

1. 从根节点开始插入
2. 如果要插入的值小于等于当前节点的值，在当前节点的左子树中插入，插入后如果左子节点的修正值小于当前节点的修正值，对当前节点进行右旋
3. 如果要插入的值大于当前节点的值，在当前节点的右子树中插入，插入后如果右子节点的修正值小于当前节点的修正值，对当前节点进行左旋
4. 如果当前节点为空节点，在此建立新的节点，该节点的值为要插入的值，左右子树为空，插入成功。

这里举个例子加以说明

如图，在已知的Treap中插入值为4的元素。找到插入的位置后，随机生成的修正值为15。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Uk0XHLdu-1574688971651)(https://i.loli.net/2019/11/25/VkhKJxyXwMCNTdP.png)]

新建的节点4与他的父节点3之间不满足堆序，对以节点3为根的子树左旋

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Sk44BPZG-1574688971652)(https://i.loli.net/2019/11/25/Whw7gaHqENXjy9D.png)]

节点4与其父节点5仍不满足最小堆序，对以节点5为根的子树右旋。

至此，节点4与其父亲2满足堆序，调整结束。

在Treap中插入元素的期望时间是 $O(logN)$ 。

代码如下：

void inser(int& p,const int x){
    if(!p){//如果没有这个点，就开一个新的点
        p=++ncnt;
        tre[p].siz=tre[p].cnt=1;
        tre[p].key=x;
        tre[p].rd=getRand();
        return;
    }
    if(tre[p].key==x){
        ++tre[p].cnt,++tre[p].siz;
        return;
    }
    int d=x>tre[p].key;
    inser(ch(p,d),x);
    if(tre[p].rd<tre[ch(p,d)].rd)rotate(p,d);
    pushup(p);
}

其中， ch() 的定义同上。

而我将 rand() 函数重新定义了一个，这样时间复杂度可能会降低一下：

inline int getRand(){
    static const int RANDMOD=1e9+9;
    static int seed=233;
    return seed=1ll*seed*998244353%RANDMOD;
}

---

删除操作

Treap的删除与普通二叉查找树不同。因为要维护堆序，比较好的方法是利用旋转的方法把要删除的结点旋转到叶结点位置，再做删除操作。

情况一，该节点为叶节点或链节点，则该节点是可以直接删除的节点。若该节点有非空子节点，用非空子节点代替该节点的，否则用空节点代替该节点，然后删除该节点。

情况二，该节点有两个非空子节点。我们的策略是通过旋转，使该节点变为可以直接删除的节点。如果该节点的左子节点的修正值小于右子节点的修正值，右旋该节点，使该节点降为右子树的根节点，然后访问右子树的根节点，继续讨论；反之，左旋该节点，使该节点降为左子树的根节点，然后访问左子树的根节点，继续讨论，知道变成可以直接删除的节点。

这里还是用一个实例：

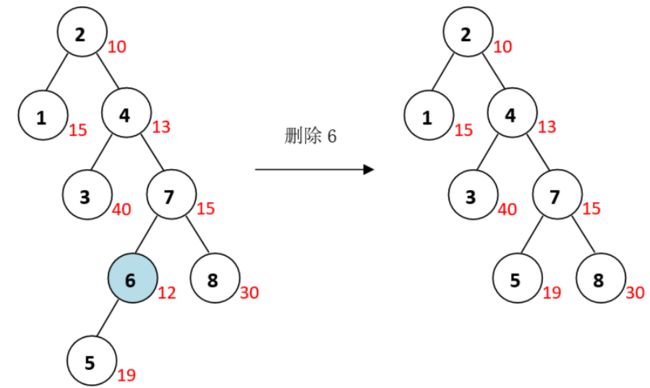
在Treap中删除值为6的元素。首先在Treap中查找6的位置。

发现节点6有两个子节点，且左子节点的修正值小于右子节点的修正值，需要右旋节点6。

旋转后，节点6仍有两个节点，右子节点修正值较小，于是左旋节点6

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U79Qp1U0-1574688971656)(https://i.loli.net/2019/11/25/hpdbawIuOfyFJV4.png)]

此时，节点6只有一个子节点，可以直接删除，用它的左子节点代替它，删除本身

删除操作的时间复杂度较高，因为涉及多次旋转及递归操作，但是期望复杂度还是 $O(logN)$

下面是代码实现

void delet(int& p,const int x){
    if(!p)return;
    if(x^tre[p].key)delet(ch(p,x>tre[p].key),x);
    else{
        if(!ch(p,0) && !ch(p,1)){//无后辈
            --tre[p].siz,--tre[p].cnt;
            if(tre[p].cnt==0)p=0;
        }
        else if(ch(p,0) && !ch(p,1)){//有左无右
            rotate(p,0);
            delet(ch(p,1),x);
        }
        else if(!ch(p,0) && ch(p,1)){//有右无左
            rotate(p,1);
            delet(ch(p,0),x);
        }
        else{//左右皆有
            int d=tre[ch(p,0)].rd<tre[ch(p,1)].rd;
            rotate(p,d);
            delet(ch(p,d^1),x);
        }
    }
    pushup(p);
}

---

其他操作

$Treap$ 还有很多操作，但是都较好理解，这里用一个例题，涉及 $6$ 种操作，每种操作可看代码自行理解：

洛谷P3369 普通平衡树

下面是代码：

#include

#define rep(i,__l,__r) for(int i=__l,i##_end_=__r;i<=i##_end_;++i)
#define fep(i,__l,__r) for(int i=__l,i##_end_=__r;i>=i##_end_;--i)
#define writc(a,b) fwrit(a),putchar(b)
#define mp(a,b) make_pair(a,b)
#define ft first
#define sd second
#define LL long long
#define ull unsigned long long
#define pii pair
// #define FILEOI

#ifdef FILEOI
	inline char fgetc(){
		#define MAXSIZE 1000
		static char buf[MAXSIZE+5],*p1=buf,*p2=buf;
		return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXSIZE,stdin),p1==p2)?EOF:*p1++;
	}
	#define cg (c=fgetc())
#else
	#define cg (c=getchar())
#endif
template<class T>inline void qread(T& x){
	char c;bool f=0;
	while(cg<'0'||'9'<c)f|=(c=='-');
	for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
	if(f)x=-x;
}
inline int qread(){
	int x=0;char c;bool f=0;
	while(cg<'0'||'9'<c)f|=(c=='-');
	for(x=(c^48);'0'<=cg&&c<='9';x=(x<<1)+(x<<3)+(c^48));
	return f?-x:x;
}
template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
inline int gcd(const int a,const int b){return b?gcd(b,a%b):a;}
inline void getInv(int inv[],const int lim,const int MOD){
	inv[0]=inv[1]=1;for(int i=2;i<=lim;++i)inv[i]=1ll*inv[MOD%i]*(MOD-MOD/i)%MOD;
}
template<class T>void fwrit(const T x){
	if(x<0)return (void)(putchar('-'),fwrit(-x));
	if(x>9)fwrit(x/10);putchar(x%10^48);
}
inline int eulerSieve(bool vis[],int prime[],const int __lim){
	int pcnt=0;vis[1]=1;
	for(int i=2;i<=__lim;++i)vis[i]=0;
	for(int i=2;i<=__lim;++i){
		if(!vis[i])prime[++pcnt]=i;
		for(int j=1;j<=pcnt&&i*prime[j]<=__lim;++j){
			vis[i*prime[j]]=true;
			if(i%prime[j]==0)break;
		}
	}
	return pcnt;
}
inline int eulerSieve(int phi[],int prime[],const int __lim){
	int pcnt=0;phi[1]=1;
	for(int i=2;i<=__lim;++i)phi[i]=0;
	for(int i=2;i<=__lim;++i){
		if(!phi[i])phi[i]=i-1,prime[++pcnt]=i;
		for(int j=1;j<=pcnt&&i*prime[j]<=__lim;++j){
			if(i%prime[j]==0){phi[i*prime[j]]=phi[i]*prime[j];break;}
			else phi[i*prime[j]]=phi[i]*phi[prime[j]];
		}
	}
	return pcnt;
}
inline int getPhi(int N){
	int ret=N;
	for(int i=2;i*i<=N;++i)if(N%i==0){ret=ret/i*(i-1);while(N%i==0)N/=i;}
	return N==1?ret:ret/N*(N-1);
}
inline LL mulMod(const LL a,const LL b,const LL mod){//long long multiplie_mod
    return ((a*b-(LL)((long double)a/mod*b+1e-8)*mod)%mod+mod)%mod;
}

const int MAXN=100000;
const int INF=2e9+5;

#define ch(i,d) tre[i].son[d]

struct treap{
    int son[2],siz,key,cnt,rd;
    treap(){siz=cnt=0;}
}tre[MAXN+5];
int ncnt;

inline void pushup(const int x){
    tre[x].siz=tre[ch(x,0)].siz+tre[ch(x,1)].siz+tre[x].cnt;
}

inline void rotate(int& x,const int d){//方向 d 的儿子上来
    int i=ch(x,d);
    ch(x,d)=ch(i,d^1);
    ch(i,d^1)=x;
    pushup(x),pushup(i);
    return (void)(x=i);
}

inline int getRand(){
    static const int RANDMOD=1e9+9;
    static int seed=233;
    return seed=1ll*seed*998244353%RANDMOD;
}

void inser(int& p,const int x){
    if(!p){
        p=++ncnt;
        tre[p].siz=tre[p].cnt=1;
        tre[p].key=x;
        tre[p].rd=getRand();
        return;
    }
    if(tre[p].key==x){
        ++tre[p].cnt,++tre[p].siz;
        return;
    }
    int d=x>tre[p].key;
    inser(ch(p,d),x);
    if(tre[p].rd<tre[ch(p,d)].rd)rotate(p,d);
    pushup(p);
}

void delet(int& p,const int x){
    if(!p)return;
    if(x^tre[p].key)delet(ch(p,x>tre[p].key),x);
    else{
        if(!ch(p,0) && !ch(p,1)){//无后辈
            --tre[p].siz,--tre[p].cnt;
            if(tre[p].cnt==0)p=0;
        }
        else if(ch(p,0) && !ch(p,1)){//有左无右
            rotate(p,0);
            delet(ch(p,1),x);
        }
        else if(!ch(p,0) && ch(p,1)){//有右无左
            rotate(p,1);
            delet(ch(p,0),x);
        }
        else{//左右皆有
            int d=tre[ch(p,0)].rd<tre[ch(p,1)].rd;
            rotate(p,d);
            delet(ch(p,d^1),x);
        }
    }
    pushup(p);
}

int getRank(const int p,const int key){
    if(!p)return -1;
    if(tre[p].key==key)return tre[ch(p,0)].siz+1;
    if(tre[p].key<key)return tre[ch(p,0)].siz+tre[p].cnt+getRank(ch(p,1),key);
    return getRank(ch(p,0),key);
}

int getKey(const int p,const int rk){
    if(!p)return -1;
    if(tre[ch(p,0)].siz>=rk)return getKey(ch(p,0),rk);
    else if(tre[ch(p,0)].siz+tre[p].cnt<rk)return getKey(ch(p,1),rk-tre[p].cnt-tre[ch(p,0)].siz);
    else return tre[p].key;
}

int getPre(const int p,const int key){
    if(!p)return -INF;
    if(tre[p].key>=key)return getPre(ch(p,0),key);
    return Max(tre[p].key,getPre(ch(p,1),key));
}

int getSuf(const int p,const int key){
    if(!p)return INF;
    if(tre[p].key<=key)return getSuf(ch(p,1),key);
    return Min(tre[p].key,getSuf(ch(p,0),key));
}

int rt;

signed main(){
#ifdef FILEOI
	freopen("rdata.out","r",stdin);
	freopen("file.out","w",stdout);
#endif
	int T=qread();
    while(T--){
        int opt=qread(),x=qread();
        switch(opt){
            case 1:
                inser(rt,x);
                break;
            case 2:
                delet(rt,x);
                break;
            case 3:
                writc(getRank(rt,x),'\n');
                break;
            case 4:
                writc(getKey(rt,x),'\n');
                break;
            case 5:
                writc(getPre(rt,x),'\n');
                break;
            case 6:
                writc(getSuf(rt,x),'\n');
                break;
        }
    }
	return 0;
}

---

调试技巧

数据结构题特别容易写挂。尤其是Treap，结点有修正值，每次插入、删除操作会引起树形态的改变，给调试带来更多困难。

这里建议在编写BST相关题目时，每写一个功能（常封装在一个函数中）就单独进行功能测试。正确了再写下一个。

在调试时，关闭srand功能，这样产生的随机数序列每次均相同，方便调试。

对于BST来说，输出中序序列是最直观检验操作是否正确的方法。写一个Debug函数，把要测试的函数放在里面做测试。

一般是先把随机生成的若干个数插入Treap，再输入某项功能所需要的数据，对相应功能做测试。