基于色彩恒常（ color constancy）特性的Frankle-McCann Retinex图像增强。

      相关随笔可见：带色彩恢复的多尺度视网膜增强算法（MSRCR）的原理、实现及应用。

     从历史的顺序上讲，本篇应该放在MSRCR之前的，只是由于现在大多论文都是描述的MSRCR，因此我也是先学习MSRCR的。

     今天，无意中找寻一些Retinex资料，搜索到一篇文章《Retinex in matlab》，原以为是MSRCR之类的matlab实现，结果仔细一看，和MSRCR算法的描述完全不同。于是找了一些资料，对Retinex的历史有了进一步了解，以下复制一些论文中的文档以供说明：

     ******************************************************************************************************************************************************************************

    文章地址：http://www.doc88.com/p-993974139685.html

    近年来，在现代生理学和心理学的启发下，美国物理学家Land等人设计出了Retinex(视网膜皮层)模型，并在符合人眼的颜色恒常性理论前提下，提出了基于Retinex的图像增强算法。这种算法建立的基础是假设人眼感知目标的亮度和颜色由环境光照和目标表面的反射光照决定，保持目标的颜色恒常性主要就是估计环境光照，并去除环境光照的影像。这样就得到了准确的目标颜色和亮度信息。由于Retinex算法具有高动态范围压缩、高色彩保真度和良好的局部细节增强等特点，引起了大量的国外学者的兴趣。为准确估计亮度分量，选取计算路径常见有一维和二维的区别。早期，Land提出选取随机路径，并对路径所经过的像素进行累加计算亮度，这种方法的缺陷在于当前像素点的亮度和随机路径上的像素亮度有关和其领域周围的像素亮度几乎无关，使得增强后的图像出现亮度不连续的现象。随后出现了两种迭代分段线性路径，即McCann99 Retinex 和Frankle-McCann Retinex,相比随机路径的Retinex而言，他们的增强效果较好。然而，他们的共同缺陷在于计算复杂度比较高，且迭代次数的选择对增强效果的影响至关重要。2004年，Ciurea和Funt发表了自动选择迭代次数的论文后，这一难题才得以解决。 Land分析了一维路径选择的缺陷，提出了二维路径的选择方式，即中心/环绕Retinex算法。这种方式下，当前像素点周围领域内像素亮度值作为计算依据，且Jobson等人严谨的证明了高斯卷积函数满足中心/环绕函数要求...........................................(以下就是SSR\MSR\MSRCR...等等）。

     ******************************************************************************************************************************************************************************

    由以上描述可见，Frankle-McCann Retinex采用了一维路径寻找方式估计亮度，而MSRCR是二维的，后者则更为复杂。

    关于FMR算法的原理呢，我一下子也讲不清，这里稍微对算法的一些过程进行简单的介绍吧。

    首先，算法的输入需要是[0,1]范围的浮点数，并且是按对数分布的，这个通常需要将[0，255]按对数方式量化到[0,1]范围内。

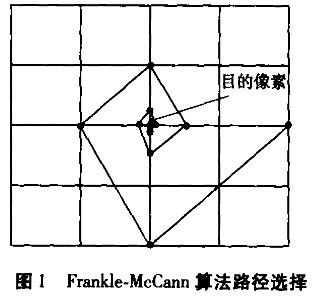
    然后按照下图所示的路径对每个点的数据进行相比、想乘、复位和平均操作。

                   

      这个我实在是说不清楚了，给几个链接大家自己看看吧：

      基于心理物理学评价和偏爱映射的高动态范围图像的色调映射算子的设计

        基于色彩恒常性的图像去雾技术

      Retinex in Matlab

      最后把处理的数据从对数域转换到[0,255]范围内（这里需要使用exp函数哦）。

      我们还是把时间放在算法效果的简要分析上。

     

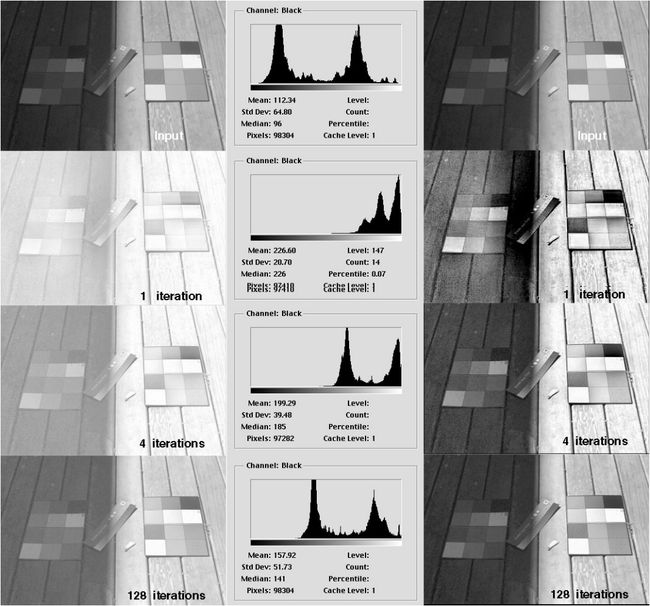
     一般情况下，可以认为FMR算法只有迭代次数一个参数。由上图可见，迭代次数越小，图像的对比度越小，连读越亮，动态压缩范围越小。迭代次数越大，图像的对比度越强烈。从直方图上看，迭代次数小时，直方图会聚集在一起，随着迭代次数等增加，直方图逐渐分布到全部动态范围内。 当迭代次数特别大时，图像会和原始图像很接近。

      我们在贴一些该算法处理的结果。

          

          

          

                       原图                                                迭代两次                                                迭代10次

     可见，对一些偏暗的图像的增强效果还是很明显。

     经过测试证明，这个算法对于我们在正常光照下拍摄的照片的处理有意想不到的效果，可以产生类似HDR的效果，贴出如下：

       

       

                               原图                                                                              处理后

   另外，该算法对偏色图像也有一定的纠偏能力，比如下图。

                                                                            

      

                                 原图                                                                             处理后

   贴出一段比较粗糙的实现该函数的matlab代码：

 

function Test()
    clear all
    rgb=imread('c:\222.jpg');%需要处理的图片
    m=size(rgb,1);
    n=size(rgb,2);
    rr=zeros(m,n);
    gg=zeros(m,n);
    bb=zeros(m,n);
    for i=1:m
        for j=1:n
            rr(i,j)=logm(double(rgb(i,j,1))+eps);
            gg(i,j)=logm(double(rgb(i,j,2))+eps);
            bb(i,j)=logm(double(rgb(i,j,3))+eps);
        end
    end
    rr=rr/max(max(rr(:)));
    gg=gg/max(max(gg(:)));
    bb=bb/max(max(bb(:)));
    rrr= retinex_frankle_mccann(rr, 4);
    ggg= retinex_frankle_mccann(gg, 4);
    bbb= retinex_frankle_mccann(bb, 4);
    for i=1:m
        for j=1:n
            rrr(i,j)=round(exp(rrr(i,j)*5.54));
            ggg(i,j)=round(exp(ggg(i,j)*5.54));
            bbb(i,j)=round(exp(bbb(i,j)*5.54));
        end
    end
    rgb=cat(3,uint8(rrr),uint8(ggg),uint8(bbb));
    rgb=max(min(rgb,255),0);
    imshow(rgb);
end

function [ Retinex ] = retinex_frankle_mccann( L, nIterations )
    global RR IP OP NP Maximum
    RR = L;
    Maximum = max(L(:));                                 % maximum color value in the image
    [nrows, ncols] = size(L);
    shift = 2^(fix(log2(min(nrows, ncols)))-1);          % initial shift
    OP = Maximum*ones(nrows, ncols);                     % initialize Old Product
    while (abs(shift) >= 1)
        for i = 1:nIterations
            CompareWith(0, shift);                         % horizontal step
            CompareWith(shift, 0);                         % vertical step
        end
        shift = -shift/2;                                 % update the shift
    end
    Retinex = NP;
end

function CompareWith(s_row, s_col)
    global RR IP OP NP Maximum
    IP = OP;
    if (s_row + s_col > 0)
        IP((s_row+1):end, (s_col+1):end) = OP(1:(end-s_row), 1:(end-s_col)) + ...
            RR((s_row+1):end, (s_col+1):end) - RR(1:(end-s_row), 1:(end-s_col));
    else
        IP(1:(end+s_row), 1:(end+s_col)) = OP((1-s_row):end, (1-s_col):end) + ...
            RR(1:(end+s_row),1:(end+s_col)) - RR((1-s_row):end, (1-s_col):end);
    end
    IP(IP > Maximum) = Maximum;                          % The Reset operation
    NP = (IP + OP)/2;                                    % average with the previous Old Product
    OP = NP;                                             % get ready for the next comparison
end

    同样，提供个编译好的文件给有兴趣研究该算法的朋友看看效果：

   http://files.cnblogs.com/Imageshop/Frankle_Mccann_Retinex.zip

 

 ***************************作者： laviewpbt   时间： 2013.4.18    联系QQ:  33184777  转载请保留本行信息*************************