谷歌的AlphaGo与柯杰的大战已经结束数日,而DeepMind承诺的50分棋谱也已经公布,而作为当前最先进的计算机“技术”,有限元方法有没有与机器学习(人工智能)进一步结合并碰发出绚丽的“火花”呢??
答案是肯定的!!!
什么是人工智能
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。 人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。人工智能从诞生以来,理论和技术日益成熟,应用领域也不断扩大,可以设想,未来人工智能带来的科技产品,将会是人类智慧的“容器”。
机器学习是人工智能的一个分支,简单地说,就是通过算法,使机器能从大量历史数据中学习规律,从而对新的样本做智能识别或对未来进行预测。
常见的机器学习算法如:
✔神经网络(Neural Network)
✔支持向量机(Support Vector Machines, SVM)Boosting
✔决策树(Decision Tree)
✔随机森林(Random Forest)
✔贝叶斯模型(Bayesian Model)等。
早期的机器学习算法由于受到理论模型和计算资源的限制,一般只能进行浅层学习,只在搜索排序系统、垃圾邮件过滤系统、内容推荐系统等地方有所应用。
而之后发生的几件事,掀起了深度学习的浪潮。一件是2006年,加拿大多伦多大学教授Hinton和他的学生Salakhutdinov在Science上发表了一篇文章,揭示了具有多个隐层的神经网络(即深度神经网络)优异的学习性能,并提出可以通过“逐层初始化”技术,来降低深度学习网络训练的难度;
第二件事是在2012年 底,Geoff Hinton 的博士生 Alex Krizhevsky、Ilya Sutskever利用卷积神经网络(Convolutional Neural Network, CNN)在图片分类的竞赛 ImageNet 上,击败了拥有众多人才资源和计算资源的Google,拿到了第一名。
如今机器学习已深入到包括语音识别,图像识别,数据挖掘等诸多领域并取得了瞩目的成绩。
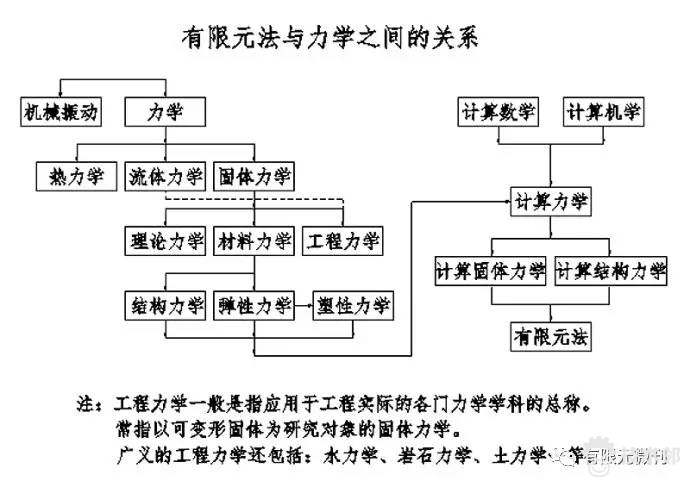
有限元法的发展简史
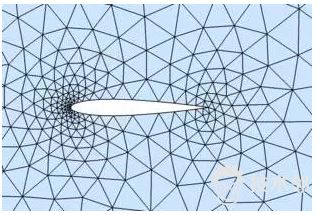
有限元方法(FEA)即有限单元法,它是一种数值分析(计算数学)工具,但不是唯一的数值分析工具。在工程领域还有其它的数值方法,如:有限差分法、边界元方法、有限体积法。
有限单元法已成为一种强有力的数值解法来解决工程中遇到的大量问题,其应用范围从固体到流体,从静力到动力,从力学问题到非力学问题。事实上,有限单元法已经成为在已知边界条件和初始条件下求解偏微分方程组的一般数值方法。
有限单元法在工程上的应用属于计算力学的范畴,而计算力学是根据力学中的理论,利用现代电子计算机和各种数值方法,解决力学中的实际问题的一门新兴学科。它横贯力学的各个分支,不断扩大各个领域中力学的研究和应用范围,同时也在逐渐发展自己的理论和方法。
神经网络与力学
其实,在深度学习浪潮掀起之前,力学和工程领域早已开始在计算力学研究中结合神经网络模型,开发出更优的算法,一个典型的例子便是有限元神经网络模型。
由于在实际工程问题中存在大量的非线性力学现象,如在结构优化问题中,需要根据需求设计并优化构件结构,是一类反问题,这些非线性问题难以用常规的方法求解,而神经网络恰好具有良好的非线性映射能力, 因而可得到比一般方法更精确的解。
将有限元与神经网络结合的方法有很多,比如针对复杂非线性结构动力学系统建模问题,可以将线性部分用有限元进行建模,非线性构件用神经网络描述(如输入非线性部件状态变量,输出其恢复力),再通过边界条件和连接条件将有限元模型部分和神经网络部分结合,得到杂交模型。
另一种方法是首先通过有限元建立多种不同的模型,再将模态特性(即最终需要达到的设计要求)作为输入变量,将对应的模型结构参数作为输入变量,训练神经网络,利用神经网络的泛化特性,得到设计参数的修正值。
结合Monter Carlo方法,进行多组有限元分析,将数据输入神经网络中进行训练,可以用来分析结构的可靠度。
已有研究成果
[1]余凯,贾磊,陈雨强,徐伟. 深度学习的昨天、今天和明天[J]. 计算机研究与发展,2013,09:1799-1804.
[2]周春桂,张希农,胡杰,谢石林. 基于有限元和神经网络的杂交建模[J]. 振动工程学报,2012,01:43-48.
[3]费庆国,张令弥. 基于径向基神经网络的有限元模型修正研究[J]. 南京航空航天大学学报,2004,06:748-752.
[4]许永江,邢兵,吴进良. 基于有限元-神经网络-Monte-Carlo的结构可靠度计算方法[J]. 重庆交通大学学报(自然科学版),2008,02:188-190+216.
未来的一些方向
1、图形显示方面(有限元与AR&VR)
随着有限元计算涉及的领域以及计算的规模不断增大,计算结果的高效、高质量的前后处理也随之成为了一个问题。
AR&VR在图形化数据展示方面,将我们从显示屏解放出来,可以以一种更加直观的方式查看计算分析数据,未来在分析结果VR展示方面,会有较大的突破。
国内也有学者已经展开了相关方面的研究,比如《虚拟现实环境中有限元前后处理功能实现》等论文,有限元虚拟处理技术(FEMVR)也开始逐步进入相关软件领域,例如:ANSYS COMSOL可以和MATLAB做交互,新版MATLAB内置了一些人工智能算法。
2、有限元与大数据、云计算
计算规模增大,伴随着计算机能力的提升,随之而来的云计算,解脱了对于计算机硬件的束缚,对于可以放开规模与数量的分析计算,有限元与大数据以及云计算的碰撞,对于未来问题的解决,将有一个质的飞跃,量变到质变的直观体现,在有限元与大数据中会有一个绚丽的展示。
3、有限元与人工智能
人工智能作为全球热的技术,与“古老”的有限元之间,相信可以在老树上发新芽,而我们可以欣喜的看到,相关的研究也已经开展,期待未来对于现实问题的解决,能有更好的更优的方案。
4、CAD数据与CAE数据的无缝对接
目前等几何分析(Isogeometric Analysis, IGA)的发展热度来看,将CAD中用于表达几何模型的NURBS基函数作为形函数,克服FEA中模型精度损失的问题,实现CAD和CAE的无缝结合,是一个很有前途和潜力的发展方向。
5、CAE与MBD的深度融合
未来CAEFEM可能会与多体动力学仿真(MBS)软件深度整合起来。实际系统中某些运动部件的弹性无法忽略,甚至是主要动力学行为的来源,所以就产生了柔性多体动力学仿真这个需求,这样只需要定义相关部件的受力和边界条件,其余的都是内部作用,仿真即节省工作量又较为真实可信。而且现在的确有很多MBS软件里面可以把部件建成弹性体,如LMS Virtual Lab,Simpack等等,但过程没有那么傻瓜;除了简单的梁、轴等零件,复杂形状的零件要依赖FEM软件事先生成的数据文件。
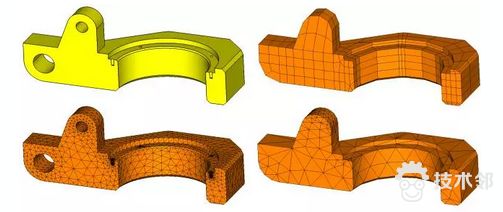
6、网格工作的智能化,傻瓜化
将来对弹性体建模可能更加傻瓜,先把刚性多体系统模型建起来,然后在建模环境(前处理)中直接make body flexible,系统可以根据这个部件的形状、材料、边界条件等选择合适的网格类型,并把运动和力的作用点couple到对应的节点(组)上。比如说汽车悬挂系统仿真,在一个工作环境下就能把某个部件的应力校核给做了,而不需要说搞多体建模的人要把边界力生成一个load case再发给专门的FEM工程师去做。
(部分来自知乎)
如何追上有限元的发展
任何技术的进步,都要在实践中展示技术的威力,有限元的发展,会随着技术的进步,特别是计算机技术的进步,在未来无论是应用软件的研究还是智能程序的开发,都将有无限的机会与可能。
积极学习新技术,新方法,在应用领域,关注有限元相关软件的新功能。
1、了解热点、跟踪前沿
2、结合实际拓展应用
3、掌握自动化相关技术
想要更多,点击此处