递归的思想就是,将大问题分解为小问题来求解,然后再将小问题分解为小小问题。这样一层一层地分解,直到问题的数据规模被分解得足够小,不用继续递归分解为止。
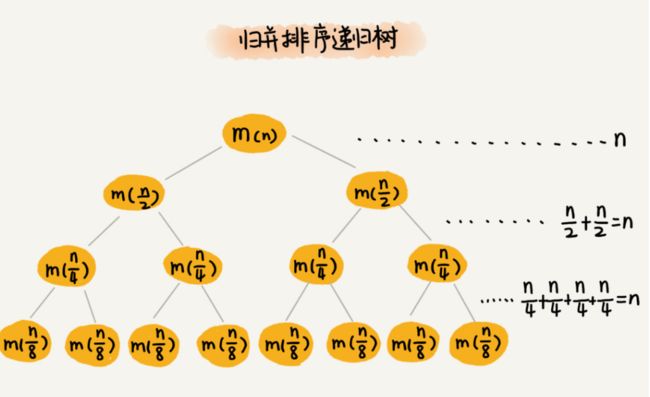
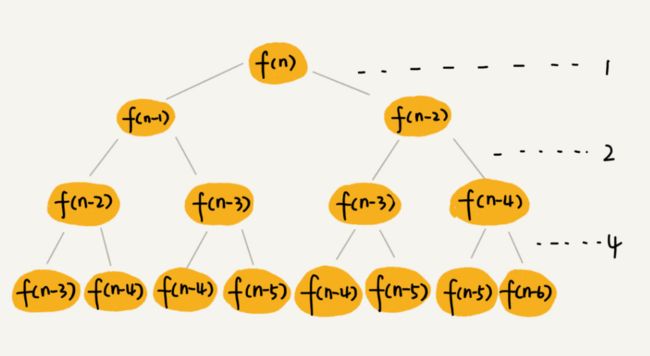
如果我们把这个一层一层的分解过程画成图,它其实就是一棵树。我们给这棵树起一个名字,叫作递归树。我这里画了一棵斐波那契数列的递归树,你可以看看。节点里的数字表示数据的规模,一个节点的求解可以分解为左右子节点两个问题的求解。
举个例子归并排序,就是将数据规模一分为二
分析斐波那契
int f(int n) { if (n == 1) return 1; if (n == 2) return 2; return f(n-1) + f(n-2); }
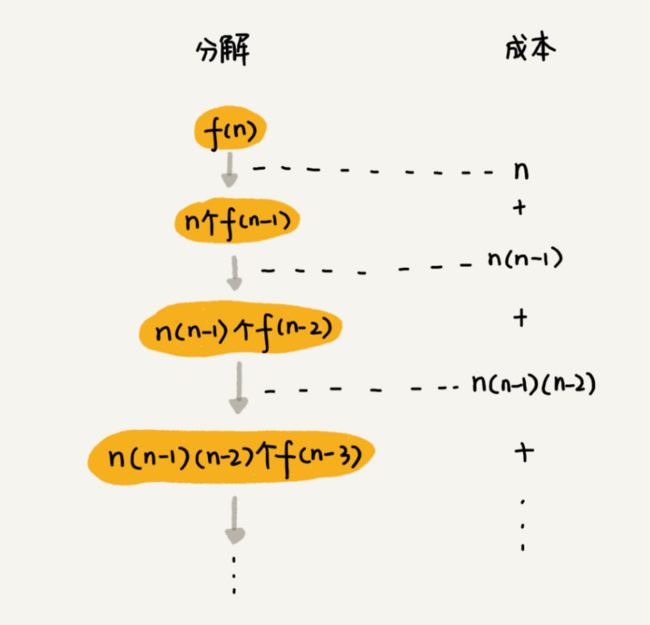
分析全排列---“如何把 n 个数据的所有排列都找出来”
1, 2, 3 1, 3, 2 2, 1, 3 2, 3, 1 3, 1, 2 3, 2, 1
递推公式
假设数组中存储的是1,2, 3...n。
f(1,2,...n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} +...+{最后一位是n, f(n-1)}。
代码实现
// 调用方式: // int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4); // k表示要处理的子数组的数据个数 public void printPermutations(int[] data, int n, int k) { if (k == 1) { for (int i = 0; i < n; ++i) { System.out.print(data[i] + " "); } System.out.println(); } for (int i = 0; i < k; ++i) { int tmp = data[i]; data[i] = data[k-1]; data[k-1] = tmp; printPermutations(data, n, k - 1); tmp = data[i]; data[i] = data[k-1]; data[k-1] = tmp; } }