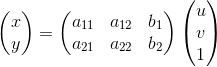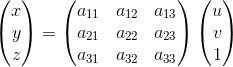引言
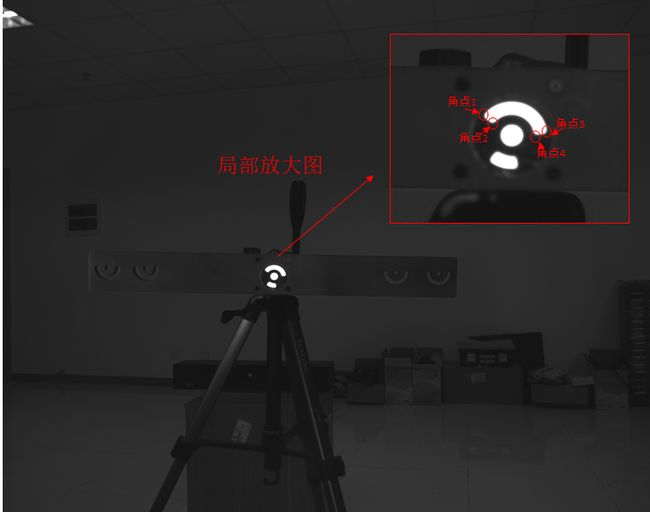
这一周主要在研究图像的放射变换与透视变换,目前出现的主要问题是需要正确识别如下图中的编码标志点圆心。
1.当倾斜角较小时:
2.倾斜角较大时:
由上面两幅图可以看出,当倾斜角较大时,中间的圆斑将变为椭圆,四周的圆环带之间的面积比关系也将出现变化,影响识别算法的正确判断。
那么如何将倾斜角如此大的编码标志点进行校正呢?这便是本篇文章需要解决的问题。
一 仿射变换与透视变换
其实一直有点没太理解「放射」俩字是啥意思,但是大家都这么叫,其实仿射变换和透视变换更直观的叫法可以叫做「平面变换」和「空间变换」或者「二维坐标变换」和「三维坐标变换」。如果这么命名的话,其实很显然,这俩是一回事,只不过一个是二维坐标(x,y),一个是三维坐标(x,y,z)。也就是:
仿射变换:
透视变换:
从另一个角度也能说明三维变换和二维变换的意思,仿射变换的方程组有6个未知数,所以要求解就需要找到3组映射点,三个点刚好确定一个平面。透视变换的方程组有8个未知数,所以要求解就需要找到4组映射点,四个点就刚好确定了一个三维空间。
仿射变换和透视变换的数学原理也不需要深究,其计算方法为坐标向量和变换矩阵的乘积,换言之就是矩阵运算。在应用层面,放射变换是图像基于3个固定顶点的变换,如图1.1所示:
图中红点即为固定顶点,在变换先后固定顶点的像素值不变,图像整体则根据变换规则进行变换同理,透视变换是图像基于4个固定顶点的变换,如图1.2所示
在OpenCV中,放射变换和透视变换均有封装好的函数,分别为:
void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
与
void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
两种变换函数形式完全相同,因此以仿射变换为例:
void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
参数InputArray src:输入变换前的图像;
参数OutputArray dst:输出变换后图像,需要初始化一个空矩阵用来保存结果,不用设定矩阵尺寸;
参数Size dsize:设置输出图像大小;
参数int flags=INTER_LINEAR:设置插值方式,默认方式为线性插值;
后两个参数不常用,在此不赘述。
关于生成变换矩阵InputArray M的函数getAffineTransform():
Mat getAffineTransform(const Point2f* src, const Point2f* dst)
参数const Point2f* src:原图的三个固定顶点
参数const Point2f* dst:目标图像的三个固定顶点
返回值:Mat型变换矩阵,可直接用于warpAffine()函数
注意,顶点数组长度超过3个,则会自动以前3个为变换顶点;数组可用Point2f[]或Point2f*表示
示例代码如下:
//读取原图
Mat I = imread("..//img.jpg");
//设置空矩阵用于保存目标图像
Mat dst;
//设置原图变换顶点
Point2f AffinePoints0[3] = { Point2f(100, 50), Point2f(100, 390), Point2f(600, 50) };
//设置目标图像变换顶点
Point2f AffinePoints1[3] = { Point2f(200, 100), Point2f(200, 330), Point2f(500, 50) };
//计算变换矩阵
Mat Trans = getAffineTransform(AffinePoints0, AffinePoints1);
//矩阵仿射变换
warpAffine(I, dst, Trans, Size(I.cols, I.rows));
//分别显示变换先后图像进行对比
imshow("src", I);
imshow("dst", dst);
waitKey();
同理,透视变换与仿射变换函数类似:
void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
生成变换矩阵函数为:
Mat getPerspectiveTransform(const Point2f* src, const Point2f* dst)
注意透视变换顶点为4个。
两种变换完整代码及结果比较:
#include
#include
using namespace std;
using namespace cv;
Mat AffineTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{
Mat dst;
Mat Trans = getAffineTransform(scrPoints, dstPoints);
warpAffine(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
return dst;
}
Mat PerspectiveTrans(Mat src, Point2f* scrPoints, Point2f* dstPoints)
{
Mat dst;
Mat Trans = getPerspectiveTransform(scrPoints, dstPoints);
warpPerspective(src, dst, Trans, Size(src.cols, src.rows), CV_INTER_CUBIC);
return dst;
}
void main()
{
Mat I = imread("..//img.jpg"); //700*438
Point2f AffinePoints0[4] = { Point2f(100, 50), Point2f(100, 390), Point2f(600, 50), Point2f(600, 390) };
Point2f AffinePoints1[4] = { Point2f(200, 100), Point2f(200, 330), Point2f(500, 50), Point2f(600, 390) };
Mat dst_affine = AffineTrans(I, AffinePoints0, AffinePoints1);
Mat dst_perspective = PerspectiveTrans(I, AffinePoints0, AffinePoints1);
for (int i = 0; i < 4; i++)
{
circle(I, AffinePoints0[i], 2, Scalar(0, 0, 255), 2);
circle(dst_affine, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);
circle(dst_perspective, AffinePoints1[i], 2, Scalar(0, 0, 255), 2);
}
imshow("origin", I);
imshow("affine", dst_affine);
imshow("perspective", dst_perspective);
waitKey();
}
可以看出,仿射变换以3个点为基准点,即使数组长度为4也仅取前3个点作为基准点;透视变换以4个点为基准点,两种变换结果不相同。应根据实际情况判断使用哪种变换方式更佳。
二 编码标志点透视变换矫正
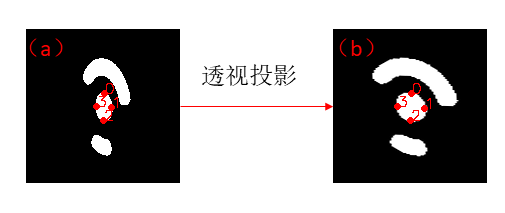
回到引言部分的问题,对于编码标志点中,我们可以以中心椭圆与坐标轴的四个交点为检测点,以椭圆的长轴为半径绘制一个理想圆,理想圆与坐标轴的交点为目标点。运用上面介绍的透视变换知识,便可以很容易的解决问题,如图2.1所示。
三 跋
文章的最后,单纯地需要感谢一下高静小朋友提供的测试样图,才得以文章正式成文。