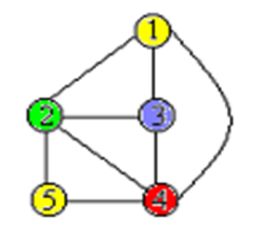
给定无向连通图和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的两个顶点有不同的颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边相连接的两个顶点着不同颜色,称这个数m为这个图的色数。求一个图的色数m称为图的m可着色优化问题。 给定一个图以及m种颜色,请计算出涂色方案数。
分析:
其实刚读这道题时,脑子里是一片混乱的,觉得无从下手,但细致分析后,t代表顶点还是能分析出来的。
使用到了邻接矩阵
还有就是color数组,也是解题的关键,要明确color数组代表的含义:color[n],大小为n,下标肯定代表顶点,里面的值代表这个顶点放的是哪种颜色。
Traceback(t)的t代表某一个顶点,这个顶点具体放哪种颜色不知道,肯定有个for循环从第一种颜色到最后一种颜色都要试一下,那么color[t]里就放当前这种颜色。OK(t)判断一下,如果可以,traceback(t+1)。
OK(t)中,t顶点和哪些顶点有联系,我就去判断这些点放置的颜色有没有和我相同,若有相同的,return false;否则,return true。
代码:
#include
#define n 5 //图有多少个点
#define m 4 //色数m
int count=0; //方案数量
int color[n]={0}; //第i个点里面放的是哪一种颜色
int a[n][n]={0,1,1,1,0, //a数组代表无向图的邻接矩阵
1,0,1,1,1,
1,1,0,1,0,
1,1,1,0,1,
0,1,0,1,0};
bool OK(int t){
for(int j=0;j