算法第四章实践报告

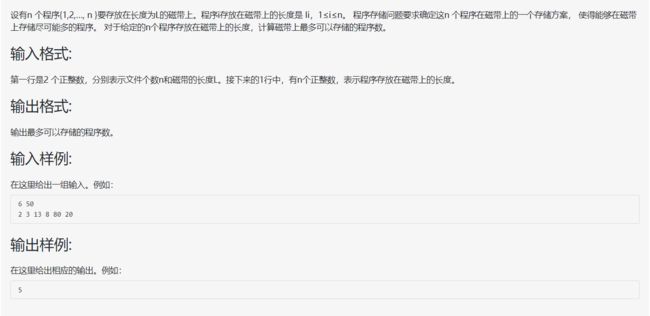
程序存储问题

题目：

解析：
这道题思路非常简单，就是选取最小的那几个程序放到磁盘里面，直到放不下为止。用贪心算法的思路来说，就是每个子问题都选取当前最小的程序，最终会得到整体的最优解。

由于使用sort函数，该算法的时间复杂度为O（nlogn）；由于没有开辟新空间，所以空间复杂度为O（1）。

具体代码如下：

#include
#include
using namespace std;
#define MAXLENGTH 1005
int program[MAXLENGTH];
int main() {
    int num; // 文件个数
    int length; // 磁带长度
    int sum = 0; // 可存的程序的长度
    int counter = 0; // 计数器
    cin >> num >> length;
    for (int i = 0; i < num; i++) {
        cin >> program[i];
    };
    sort(program, program + num);
    for (int i = 0; i < num; i++) {
        sum += program[i];
        if (sum <= length) {
            counter++;
        }
        else {
            break;
        }
    }
    cout << counter << endl;
    system("pause");
    return 0;
}

---

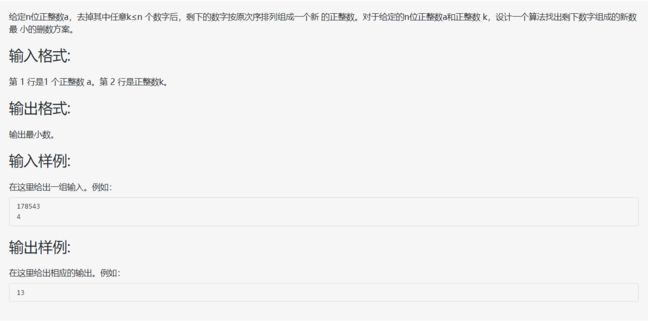
删数问题

题目如下：

解析：
拿到题的时候，应该第一反应是删除这行数字中最大的一个。比如样例：

1. 178543中删去最大的一个，即8，剩下的数字为17543；
2. 17543中删去最大的一个，即7，剩下的数字为1543；
3. 1543中删去最大的一个，即5，剩下的数字为143；
   ····

以此类推，我们可以发现：每次删除的数，都是从第一个数字开始的升序序列的最后一个数！
这样我们的贪心策略就可以变成：每次从第一个数字开始，删去当前的升序序列的最大一个数，一直删到规定的k个数为止。这样，就可以算是由当前的最优解得到最后的最优解。

具体代码如下：

#include
#include
using namespace std;
int main() {
    string s;
    int num;// 删除的数字个数
    cin >> s >> num;
    while (num > 0) {
        for (int i = 0; i < s.size(); i++) {
            if (s[i] > s[i + 1]) {
                s.erase(i, 1);
                break;
            }
        }
        num--;
    };
    
    //除去前导0
    for (int i = 0; i < s.size(); i++) {
        if (s[0] == '0') {
            s.erase(0, 1);
        }
    }
    cout << s << endl;
    system("pause");
    return 0;
}

---

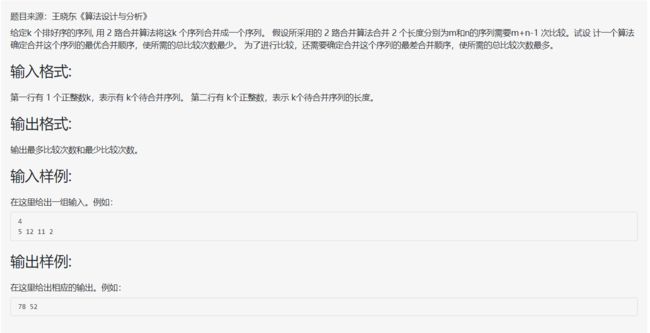
最优合并问题

题目如下：

解析：
这道题的贪心策略就是每次选取最小/最大的两个数字，从而得到最小/最大的比较次数。
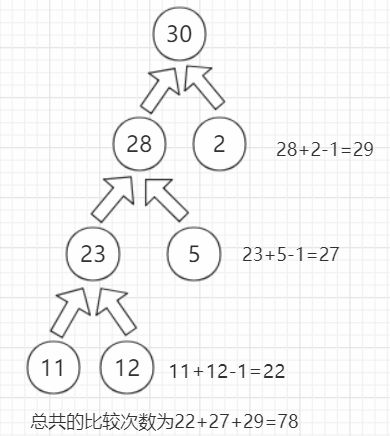
由题意可知，其实是一个哈夫曼树问题：
合并最小的节点，可以获得最小的合并比较次数：

合并最大的节点，可以获得最大的合并比较次数：

具体代码如下：
（实现时使用了stl的优先队列，非常方便）：

#include
#include
using namespace std;
priority_queue q1; // 从大到小的优先队列
priority_queue, greater > q2; // 从小到大的优先队列
int main() {
    int num;
    int arr[1005];
    cin >> num;
    int maxtime = 0;
    int mintime = 0;
    for (int i = 0; i < num; i++) {
        cin >> arr[i];
        q1.push(arr[i]);
        q2.push(arr[i]);
    }
    
    // 求出最大的比较次数
    while (true) {
        if (q1.size() == 1) {
            break;
        }
        else {
            int tmp1 = q1.top();
            q1.pop();
            int tmp2 = q1.top();
            q1.pop();
            maxtime += tmp1 + tmp2 - 1;
            q1.push(tmp1+tmp2);
        }
    }
    
    // 求出最小的比较次数
    while (true) {
        if (q2.size() == 1) {
            break;
        }
        else {
            int tmp1 = q2.top();
            q2.pop();
            int tmp2 = q2.top();
            q2.pop();
            mintime += tmp1 + tmp2 - 1;
            q2.push(tmp1+tmp2);
        }
    }
    cout << maxtime << " " << mintime << endl;
    system("pause");
    return 0;
}

---

结对编程小结

在这次结对编程中和队友依旧配合良好，在我提供了思路或者WA的时候会及时帮我纠正问题所在，以及在最后一题中提出使用优先队列的做法，使代码变得整洁，快速得出了我们所要的答案。谢谢队友再次带飞我。