1. 线性混合(Linear Blending):
前面提到过加权平均法,每个个体学习器的权重不再相等,看起来就像是对每个个体学习器做一个线性组合
我们首先用训练数据训练出所有的,然后再做线性回归求出。注意到这里要求,来个拉格朗日函数?其实不用,通常我们可以忽略这个条件。以二分类为例如果αi小于0,相当于把模型反过来用。
- 如何得到?
这里我们将个体学习器称为初级学习器,用于结合的学习器称为次级学习器。首先从数据集中训练出初级学习器,然后用初级学习器生成一个新的数据集用于训练次级学习器。注意为了防止过拟合,我们需要在训练集上做训练得到初级学习器,而在验证集上比较不同a的好坏。最终模型则在所有的数据上进行训练(数据量多可能使得模型效果更好)
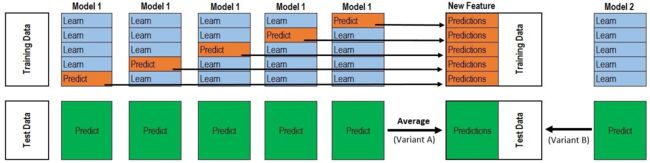
2. Stacking(实际上就是把Blending组合起来)
Stacking做法和Linear Blending类似,首先从数据集中训练出初级学习器,然后”生成“一个新的数据集用于训练次级学习器。为了防止过拟合,采用K折交叉验证法求解。
假设采用5折交叉验证,每个模型都要做满5次训练和预测,对于每一次:
- 从80%的数据训练得到一个模型ht,然后预测训练集剩下的那20%,同时也要预测测试集。
- 每次有20%的训练数据被预测,5次后正好每个训练样本都被预测过了。
- 每次都要预测测试集,因此最后测试集被预测5次,最终结果取5次的平均。
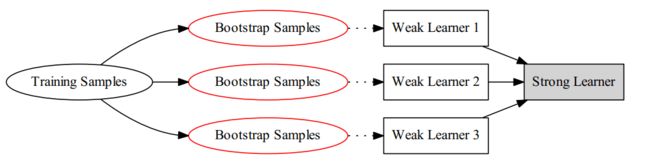
3. Bagging
除了分类器不同外还可以对训练样本进行采样,使采样出的每个子集都完全不同。但是如果样本过少,互斥地选择样本采样的样本数更少,不能保证训练出的学习器好。此时可以考虑使用有重叠的采样子集(相互之间有关联)。对此,Bagging算法采用Bootstrap(也称为自助法)进行采样。
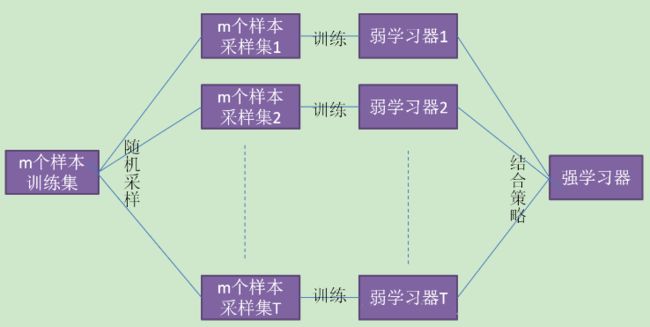
- Bootstrap算法:
Bootstrap为有放回的抽样,每次从m个样本的数据集D中抽取一个,重复m次,最终得到包含m个样本的采样集D'(可见需要训练的样本数其实跟原数据集一样)。显然,数据集D中有一部分样本会在D'中出现,而一部分不会。可以做一个简单的估计,样本在m次采样过程中始终不会被采样到的概率是,也就是说,每个基学习器用到了初始训练集中约63.2%的样本,剩下的36.8%的样本可以用来做”袋外估计“(out-of-bag estimate),即这些没有用到的样本可以来做验证集
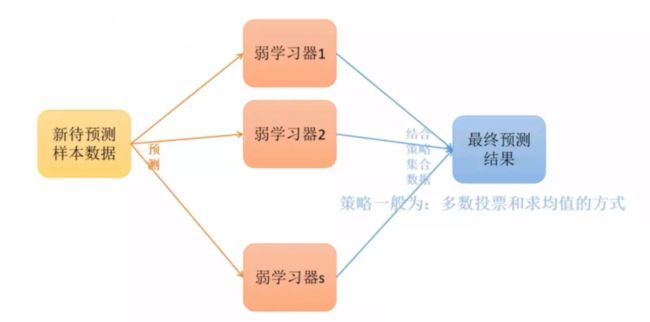
最后得到T个,用均匀混合法/多数投票得到最后的模型。
从方差和偏差的角度看,Bagging主要降低的是方差,如果基算法对随机性比较敏感,那么bagging的结果会比较好。如不剪枝的决策树、神经网络。
- Bagging方法的弱学习器可以是基本的算法模型:Linear、Ridge、Lasso、Logistic、Softmax、ID3、C4.5、CART、SVM、KNN等。