LintCode 线段树系列问题（线段树的构造，线段树的构造||，线段树的查询，线段树的查询II,线段树的修改）

线段树(又称区间树), 是一种高级数据结构，他可以支持这样的一些操作:

• 查找给定的点包含在了哪些区间内
• 查找给定的区间包含了哪些点

线段树的构造

题目

线段树是一棵二叉树，他的每个节点包含了两个额外的属性start和end用于表示该节点所代表的区间。start和end都是整数，并按照如下的方式赋值:

• 根节点的 start 和 end 由 build 方法所给出。
• 对于节点 A 的左儿子，有 start=A.left, end=(A.left + A.right) / 2。
• 对于节点 A 的右儿子，有 start=(A.left + A.right) / 2 + 1, end=A.right。
• 如果 start 等于 end, 那么该节点是叶子节点，不再有左右儿子。

实现一个 build 方法，接受 start 和 end 作为参数, 然后构造一个代表区间 [start, end] 的线段树，返回这棵线段树的根。

代码

/**
 * Definition of SegmentTreeNode:
 * public class SegmentTreeNode {
 *     public int start, end;
 *     public SegmentTreeNode left, right;
 *     public SegmentTreeNode(int start, int end) {
 *         this.start = start, this.end = end;
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     *@param start, end: Denote an segment / interval
     *@return: The root of Segment Tree
     */
    public SegmentTreeNode build(int start, int end) {
        // write your code here
        if(start > end) {  // check core case
            return null;
        }
       
        SegmentTreeNode root = new SegmentTreeNode(start, end);
       
        if(start < end) {
            int mid = (start + end) / 2;
            root.left = build(start, mid);
            root.right = build(mid+1, end);
        }
        return root;
    }
}

线段树的构造 II

题目

跟上题类似，增加一个属性max，记录区间最大值

代码

/**
 * Definition of SegmentTreeNode:
 * public class SegmentTreeNode {
 *     public int start, end, max;
 *     public SegmentTreeNode left, right;
 *     public SegmentTreeNode(int start, int end, int max) {
 *         this.start = start;
 *         this.end = end;
 *         this.max = max
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     *@param A: a list of integer
     *@return: The root of Segment Tree
     */
    public SegmentTreeNode build(int[] A) {
        // write your code here
        return buildTree(0, A.length - 1, A);
    }

    public SegmentTreeNode buildTree(int start, int end, int[] A) {
        if (start > end)
            return null;

        if (start == end) {
            return new SegmentTreeNode(start, end, A[start]);
        }
        
        SegmentTreeNode node = new SegmentTreeNode(start, end, A[start]);
        int mid = (start + end) / 2;
        node.left = this.buildTree(start, mid, A);
        node.right = this.buildTree(mid + 1, end, A);
        node.max = Math.max(node.left.max, node.right.max);
        
        return node;
    }
}

线段树的查询

题目

对于一个有n个数的整数数组，在对应的线段树中, 根节点所代表的区间为0-n-1, 每个节点有一个额外的属性max，值为该节点所代表的数组区间start到end内的最大值。

为SegmentTree设计一个 query 的方法，接受3个参数root, start和end，线段树root所代表的数组中子区间[start, end]内的最大值。

样例
对于数组 [1, 4, 2, 3], 对应的线段树为：
query(root, 1, 1), return 4

query(root, 1, 2), return 4

query(root, 2, 3), return 3

query(root, 0, 2), return 4

Paste_Image.png

代码

/**
 * Definition of SegmentTreeNode:
 * public class SegmentTreeNode {
 *     public int start, end, max;
 *     public SegmentTreeNode left, right;
 *     public SegmentTreeNode(int start, int end, int max) {
 *         this.start = start;
 *         this.end = end;
 *         this.max = max
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     *@param root, start, end: The root of segment tree and 
     *                         an segment / interval
     *@return: The maximum number in the interval [start, end]
     */
    public int query(SegmentTreeNode root, int start, int end) {
        // write your code here
        if(root == null)
        {
            return Integer.MIN_VALUE;
        }
        
        if(start == root.start && root.end == end) { // 相等 
            return root.max;
        }
        
        
        
        int mid = (root.start + root.end)/2;
        int leftmax = Integer.MIN_VALUE, rightmax = Integer.MIN_VALUE;
        // 左子区
        if(start <= mid) {
            if( mid < end) { // 分裂 
                leftmax =  query(root.left, start, mid);
            } else { // 包含 
                leftmax = query(root.left, start, end);
            }
            // leftmax = query(root.left, start, Math.min(mid,end));
        }
        // 右子区
        if(mid < end) { // 分裂 3
            if(start <= mid) {
                rightmax = query(root.right, mid+1, end);
            } else { //  包含 
                rightmax = query(root.right, start, end);
            }
            //rightmax = query(root.right, Math.max(mid+1,start), end);
        }  
        // else 就是不相交
        return Math.max(leftmax, rightmax);
    }
}

线段树查询 II

题目

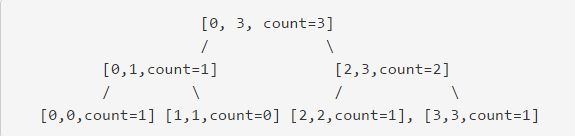
对于一个数组，我们可以对其建立一棵 线段树, 每个结点存储一个额外的值 count 来代表这个结点所指代的数组区间内的元素个数. (数组中并不一定每个位置上都有元素)

实现一个 query 的方法，该方法接受三个参数 root, start 和 end, 分别代表线段树的根节点和需要查询的区间，找到数组中在区间[start, end]内的元素个数。

样例
对于数组 [0, 空，2, 3], 对应的线段树为：

Paste_Image.png

query(1, 1), return 0

query(1, 2), return 1

query(2, 3), return 2

query(0, 2), return 2

代码

/**
 * Definition of SegmentTreeNode:
 * public class SegmentTreeNode {
 *     public int start, end, count;
 *     public SegmentTreeNode left, right;
 *     public SegmentTreeNode(int start, int end, int count) {
 *         this.start = start;
 *         this.end = end;
 *         this.count = count;
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     *@param root, start, end: The root of segment tree and 
     *                         an segment / interval
     *@return: The count number in the interval [start, end]
     */
    public int query(SegmentTreeNode root, int start, int end) {
        // write your code here
        if(start > end || root==null)
            return 0;
        if(start <= root.start && root.end <= end) { // 相等 
            return root.count;
        }
        
        int mid = (root.start + root.end)/2;
        int leftsum = 0, rightsum = 0;
        // 左子区
        if(start <= mid) {
            if( mid < end) { // 分裂 
                leftsum =  query(root.left, start, mid);
            } else { // 包含 
                leftsum = query(root.left, start, end);
            }
        }
        // 右子区
        if(mid < end) { // 分裂 3
            if(start <= mid) {
                rightsum = query(root.right, mid+1, end);
            } else { //  包含 
                rightsum = query(root.right, start, end);
            } 
        }  
        // else 就是不相交
        return leftsum + rightsum;
    }
}

线段树的修改

题目

对于一棵 最大线段树, 每个节点包含一个额外的 max 属性，用于存储该节点所代表区间的最大值。

设计一个 modify 的方法，接受三个参数 root、 index 和 value。该方法将 root 为跟的线段树中 [start, end] = [index, index] 的节点修改为了新的 value ，并确保在修改后，线段树的每个节点的 max 属性仍然具有正确的值。

样例
对于线段树:

Paste_Image.png

代码

/**
 * Definition of SegmentTreeNode:
 * public class SegmentTreeNode {
 *     public int start, end, max;
 *     public SegmentTreeNode left, right;
 *     public SegmentTreeNode(int start, int end, int max) {
 *         this.start = start;
 *         this.end = end;
 *         this.max = max
 *         this.left = this.right = null;
 *     }
 * }
 */
public class Solution {
    /**
     *@param root, index, value: The root of segment tree and 
     *@ change the node's value with [index, index] to the new given value
     *@return: void
     */
    public void modify(SegmentTreeNode root, int index, int value) {
        // write your code here
        if(root.start >= index && root.end <= index) { // 查找到
            root.max = value;
            return;
        }
        
        // 查询
        int mid = (root.start + root.end) / 2;
        if(root.start <= index && index <=mid) {
            modify(root.left, index, value);
        }
        
        if(mid < index && index <= root.end) {
            modify(root.right, index, value);
        }
        //更新
        root.max = Math.max(root.left.max, root.right.max);
    }
}