查找最小生成树：普里姆算法算法（Prim）算法

一、算法介绍

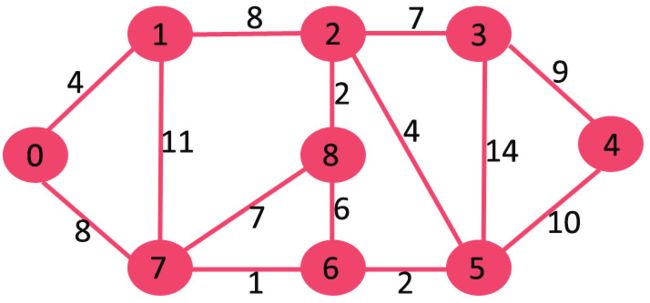
　　普里姆算法（Prim's algorithm），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。像 Kruskal算法一样，Prim算法也是贪婪算法。

二、Prim算法思想

　　Prim算法的思想很简单，一棵生成树意味着必须连接所有顶点。因此必须将两个不相交的顶点子集连接起来才能生成生成树 。并且它们必须以最小的权重边连接，以使其成为最小的生成树（MST）。它从一棵空的生成树开始。这个想法是维持两组顶点。第一组包含 MST 中已包含的顶点，另一组包含尚未包含的顶点。在每一步中，它都会考虑连接两组的所有边，并从这些边中选取最小权重边。选取完边后，它将边的另一个顶点点移动到包含 MST 的集合。

　　将图中的两组顶点连接起来的一组边线在图论中称为割，割是表示图的一组顶点中的两个不相交的子集。因此，在Prim算法的每一步中，都会去找到一个割线（分为两组，一组包含MST中已经包含的顶点，另一组包含其余的顶点），从割中选取最小权重边，然后将此顶点包含到 MST 的集合中。

步骤：

1）创建一个集合 mstSet，该集合跟踪已包含在 MST 中的顶点。

2）为输入图中的所有顶点分配一个键值。将所有键值初始化为 INFINITE。将第一个顶点的键值指定为 0，以便首先选择它。

3）虽然当前的 mstSet 不包括所有顶点：

　　a）选择一个在 mstSet 中不存在且具有最小键值的顶点 u。

　　b）将 u 包含到 mstSet 中。

　　c）更新 u 的所有相邻顶点的键值。要更新键值，需遍历所有相邻的顶点。对于每个相邻顶点 v，如果边 u-v 的权重小于 v 的先前键值，则将键值更新为 u-v 的权重。

　　下面用一个例子来理解：

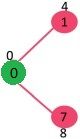
 　　集合 mstSet 最初为空，并且分配给顶点的键为 {0，INF，INF，INF，INF，INF，INF，INF}，其中 INF 表示无穷大。现在选择具有最小键值的顶点。选择顶点0，将其包含在 mstSet 中。因此，mstSet 变为 {0}。在包含到 mstSet 之后，更新相邻顶点的键值。0的相邻顶点是 1 和 7。1 和 7 的关键值更新为 4 和 8。下面的子图显示了顶点及其关键值，仅显示了具有有限关键值的顶点。MST 中包含的顶点显示为绿色。

 　　选择具有最小键值且尚未包含在 MST 中的顶点（不在 mstSet 中）。选择顶点1并将其添加到 mstSet。因此，mstSet 现在变为 {0，1}。更新相邻顶点1的键值，顶点2的键值变为 8。

 

 

 

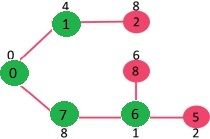
 　　选择具有最小键值且尚未包含在 MST 中的顶点（不在 mstSet 中）。我们可以选择顶点7 或 顶点2，让顶点7被选择。因此，mstSet 现在变为 {0，1，7}。更新相邻顶点7的关键值。顶点 6 和 8 的关键值变得有限（分别为 1 和 7）。

 

 

 　　选择具有最小键值且尚未包含在 MST 中的顶点（不在 mstSet 中）。选择了顶点6。这样 mstSet 现在变成 {0，1，7，6}。更新相邻顶点6的关键点值。更新顶点 5 和 8 的关键点值。

 

 

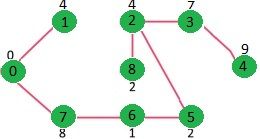
　　重复上述步骤，直到 mstSet 包含给定图的所有顶点。最后，我们得到下图。

 

 

三、算法代码

Prim算法：

 1     /**
 2      * 为使用邻接矩阵表示的图构造和打印MST
 3      *
 4      * @param graph 图的邻接矩阵
 5      */
 6     public void primMST(int[][] graph) {
 7         /* 存储构造的MST */
 8         int[] parent = new int[V];
 9 
10         /* 用于选择切割中最小权重的边的关键值 */
11         int[] key = new int[V];
12 
13         /* 表示尚未包含在MST中的一组顶点 */
14         Boolean[] mstSet = new Boolean[V];
15 
16         /* 将所有键初始化为INFINITE */
17         for (int i = 0; i < V; i++) {
18             key[i] = Integer.MAX_VALUE;
19             mstSet[i] = false;
20         }
21 
22         /* 首先把一个顶点包含在MST中 */
23         key[0] = 0;     // 设置键0，以便此顶点被选为第一个顶点
24         parent[0] = -1; // 第一个节点始终是MST的根
25 
26         for (int count = 0; count < V-1; count++) {
27             /* 从顶点集合中选择尚未包含在MST中最小关键点顶点 */
28             int u = minKey(key, mstSet);
29 
30             /* 将选取的顶点添加到MST集 */
31             mstSet[u] = true;
32 
33             // graph[u][v]仅对于m的相邻顶点为非零
34             // 对于MST中尚未包含的顶点，mstSet[v]为false
35             // 仅当graph[u][v]小于key[v]时更新密钥
36             for (int v = 0; v < V; v++) {
37                 if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
38                     parent[v] = u;
39                     key[v] = graph[u][v];
40                 }
41             }
42         }
43 
44         /* 打印构造的MST */
45         printMST(parent, graph);
46     }

　　选取尚未包含在 MST 的最小关键值的顶点。

 1     /**
 2      * 用于从尚未包含在MST中的一组顶点中查找具有最小关键值的顶点
 3      *
 4      * @param key
 5      * @param mstSet
 6      * @return
 7      */
 8     private int minKey(int[] key, Boolean[] mstSet) {
 9         /* 初始化最小值 */
10         int min = Integer.MAX_VALUE, min_index = -1;
11 
12         for (int v = 0; v < V; v++) {
13             if (!mstSet[v] && key[v] < min) {
14                 min = key[v];
15                 min_index = v;
16             }
17         }
18 
19         return min_index;
20     }

　　使用邻接矩阵的 Prim 算法中找到所有最小权边共需时间复杂度为 O(V²)。使用简单的二叉堆与邻接表来表示的话，算法的时间复杂度可减少至 O(E·log₂V)，其中 E 为图的边集，V 为图的点集。

 

本文源代码：

 

  1 package algorithm.mst;
  2 
  3 public class PrimAlgorithm {
  4     private static int V = 5;
  5 
  6     /**
  7      * 用于从尚未包含在MST中的一组顶点中查找具有最小关键值的顶点
  8      * O(V)
  9      *
 10      * @param key
 11      * @param mstSet
 12      * @return
 13      */
 14     private int minKey(int[] key, Boolean[] mstSet) {
 15         /* 初始化最小值 */
 16         int min = Integer.MAX_VALUE, min_index = -1;
 17 
 18         for (int v = 0; v < V; v++) {
 19             if (!mstSet[v] && key[v] < min) {
 20                 min = key[v];
 21                 min_index = v;
 22             }
 23         }
 24 
 25         return min_index;
 26     }
 27 
 28     /**
 29      * 打印构造的MST
 30      * @param parent
 31      * @param graph
 32      */
 33     private void printMST(int[] parent, int[][] graph) {
 34         System.out.println("Edge \t Weight");
 35         for (int i = 1; i < V; i++) {
 36             System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
 37         }
 38     }
 39 
 40     /**
 41      * 为使用邻接矩阵表示的图构造和打印MST
 42      *
 43      * @param graph 图的邻接矩阵
 44      */
 45     public void primMST(int[][] graph) {
 46         /* 存储构造的MST */
 47         int[] parent = new int[V];
 48 
 49         /* 用于选择切割中最小权重的边的关键值 */
 50         int[] key = new int[V];
 51 
 52         /* 表示尚未包含在MST中的一组顶点 */
 53         Boolean[] mstSet = new Boolean[V];
 54 
 55         /* 将所有键初始化为INFINITE */
 56         for (int i = 0; i < V; i++) {
 57             key[i] = Integer.MAX_VALUE;
 58             mstSet[i] = false;
 59         }
 60 
 61         /* 首先把一个顶点包含在MST中 */
 62         key[0] = 0;     // 设置键0，以便此顶点被选为第一个顶点
 63         parent[0] = -1; // 第一个节点始终是MST的根
 64 
 65         for (int count = 0; count < V-1; count++) {
 66             /* 从顶点集合中选择尚未包含在MST中最小关键点顶点 */
 67             int u = minKey(key, mstSet);
 68 
 69             /* 将选取的顶点添加到MST集 */
 70             mstSet[u] = true;
 71 
 72             // graph[u][v]仅对于m的相邻顶点为非零
 73             // 对于MST中尚未包含的顶点，mstSet[v]为false
 74             // 仅当graph[u][v]小于key[v]时更新密钥
 75             for (int v = 0; v < V; v++) {
 76                 if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
 77                     parent[v] = u;
 78                     key[v] = graph[u][v];
 79                 }
 80             }
 81         }
 82 
 83         /* 打印构造的MST */
 84         printMST(parent, graph);
 85     }
 86 
 87     public static void main(String[] args) {
 88         /* 创建一个图的邻接矩阵
 89                 2      3
 90             (0) -- (1) -- (2)
 91              |    /  \     |
 92             6|  8/    \5   |7
 93              |  /      \   |
 94             (3) --------- (4)
 95                     9
 96          */
 97         PrimAlgorithm t = new PrimAlgorithm();
 98         int[][] graph = new int[][] {
 99                 { 0, 2, 0, 6, 0 },
100                 { 2, 0, 3, 8, 5 },
101                 { 0, 3, 0, 0, 7 },
102                 { 6, 8, 0, 0, 9 },
103                 { 0, 5, 7, 9, 0 }
104         };
105 
106         // 打印解决方案
107         t.primMST(graph);
108     }
109 }

View Code