title: 理解KMP
date: 2017-12-14 12:58:03
tags:
是什么?
Knuth-Morris-Pratt 算法(简称 KMP)是解决字符串匹配问题的常用算法之一,这个算法是由高德纳(Donald Ervin Knuth)和沃恩 · 普拉特在 1974 年构思,同年詹姆斯 ·H· 莫里斯也独立地设计出该算法,最终三人于 1977 年联合发表。
干什么的?
KMP算法一般用于解决字符串匹配问题
有主字符串P = “abcda”, 模式串 T=“cda”。问T是否出现在P中?若出现过指出出现的起始位置。
暴力匹配
介绍完KMP后回到字符串匹配这个问题,我第一次看到这个问题时,想到的最简单也就是最无脑的暴力匹配:
维护两个下标 i j.分别用来标识正在匹配字符在 P , T 两个字符串中的索引。�遍历字符进行匹配, T[j] 在与 P[i] 匹配的过程中若出现不匹配的字符,就让 i 退回 j 个(i = i - j + 1),而 j 则回退到开始即 j = 0�。
以下是Java代码:
public class KMP {
public static void main(String[] args) {
System.out.print(fKMP("abadda", "da"));
}
static int fKMP(String p, String t) {
int i = 0;
int j = 0;
int pL = p.length();
int tL = t.length();
while (i < pL && j < tL) {
if (p.charAt(i) == t.charAt(j)) {
i += 1;
j += 1;
} else {
i = i - j + 1;
j = 0;
}
}
if (tL == j) {
return i - j;
}
return -1;
}
}
我们来分析这个算法的时间复杂度O(mn),显然这样的复杂度在有些情况下确实有点效率不高:当T中有字符串重复出现那么,有些匹配就是徒劳的,分析他之所以不高的原因是:当某一位字符匹配�失败的时候 j 和 i 都会回退,而在�回退的时候有些回退是不必要的。�因为在以及匹配完成的字符里若出现过重复的,再进行一次匹配则是徒劳的。
改进
如何才能避免出现对已经比对过得字符串�重复的进行比对呢?
我们根据经验试着推出
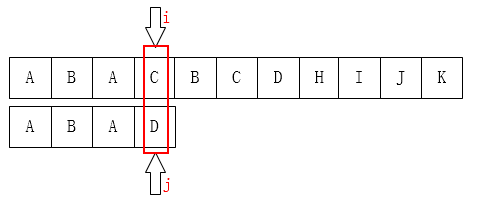
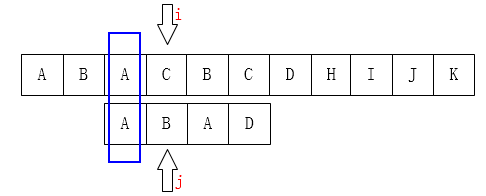
上图中 p[3] 和 t[3] 比对失配后,按照暴力匹配的流程 i 会回滚p[1],j回滚到 t [0],但是回滚后p[1]和必然是不匹配的,因为在回滚前已经匹配过的 ABA 中 A 已经出现过一次,所以将模式串向右移动 2 个位置正好。
�移动后 i 还是不变,而 j 则是回滚到了 t[1]。
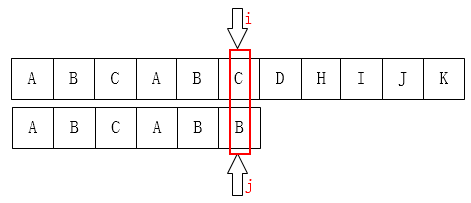
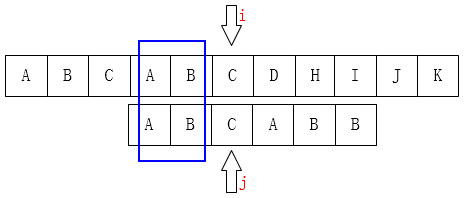
上面这个在匹配过程中,在匹配到 p[5] 与 t[5] 时�失配,我们发现 AB 在模式串中出现过两次,我们把模式串向前移动 3 个位置。接着匹配
移动完成后 i 的位置不动依然在 p[5] ,�而 j 则是回滚到了t[2]。
总结规律:模式串 t 中,若存在一些相同的字符,而我们模式串移动的位置(其实就是j的位置移动)则和这些重复出现的字符串长度有关.
next数组
在KMP�算法中有个很重要的�的概念那就是next数组;关于 next 数组的定义:该字符串在某一位字符前左前缀与右前缀两个集合中,重合�元素中长度最长元素的长度。
如:
字符串ABAAB,其最左前缀(不包括最后一个字符)有{A,AB,ABA,ABAA},最右前缀(不包括第一个字符)有{B,AB,AAB,BAAB}。
当i=0时,字符串为"A",,此时最左前缀为空,最右前缀也为空,next[0]==空;
当i=1时,字符串为"AB",,此时最左前缀为{A},最右前缀为{B},两个结合重合的元素为空 所以next[1]==0;
当i=2时,字符串为"ABA",,此时最左前缀为{A,AB},最右前缀为A,BA},重合的元素为 A 所以next[2]==1;
当i=3时,字符串为"ABAA",,此时最左前缀为{A,AB,ABA},最右前缀为{A,AA,BAA},两个集合重合的元素为 A 所以next[3]==1;
当i=4时,字符串为"ABAAB",,此时最左前缀为{A,AB,ABA,ABAA},最右前缀为{B,AB,AAB,BAAB},两个集合中重合的元素A、AB。 最长为AB, 所以next[4]==2;
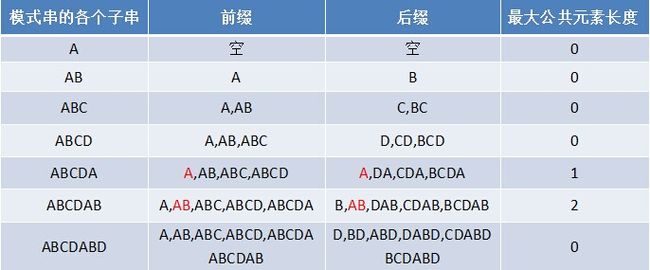
对于字符串“ABCDABD”:
这样的方法们就能轻而易举的算出next数组。
但是此时的next数组和真正的数组还有一些区别:
我们在求next数组的时候,对当前字符是不关心的,我们只关心这个字符之前最大公共元素的长长度。所以将刚才的next数组向右移动一位。空位补-1。
这样符合KMP的next数组就求出来了。
以下是求出next数组的Java代码
private static int[] getNext(String t) {
int next[] = new int[t.length()];
int p_len = t.length();
int i = 0;
int j = -1;
next[0] = -1;
while (i < p_len - 1) {
if (j == -1 || t.charAt(i) == t.charAt(j)) {
i++;
j++;
next[i] = j;
} else {
j = next[j];
}
}
return next;
}
完整代码
public class KMP {
public static void main(String[] args) {
System.out.print(fKMP("“abcda”", "bcda"));
}
static int fKMP(String p, String t) {
int i = 0;
int j = 0;
int pL = p.length();
int tL = t.length();
int[] next = getNext(t);
while (i < pL && j < tL) {
if (j == -1 || p.charAt(i) == t.charAt(j)) {
i += 1;
j += 1;
} else {
j = next[j];
}
}
if (tL == j) {
return i - j;
}
return -1;
}
private static int[] getNext(String t) {
int next[] = new int[t.length()];
int p_len = t.length();
int i = 0;
int j = -1;
next[0] = -1;
while (i < p_len - 1) {
if (j == -1 || t.charAt(i) == t.charAt(j)) {
i++;
j++;
next[i] = j;
} else {
j = next[j];
}
}
return next;
}
}
一句话
一句话来总结KMP:对于KMP算法来说只有当模式串中出现重复字符,KMP算法才能发挥它的作用。
参考
https://www.61mon.com/index.php/archives/183/
https://www.cnblogs.com/zhangtianq/p/5839909.html
s
http://www.cnblogs.com/yjiyjige/p/3263858.html