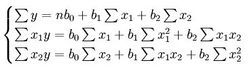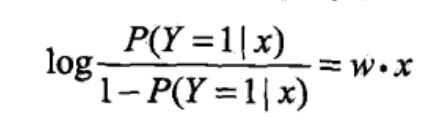监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。
回归分析(regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。运用十分广泛,回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;在线性回归中,按照因变量的多少,可分为简单回归分析和多重回归分析;按照[自变量]和[因变量]之间的关系类型,可分为[线性回归]分析和[非线性回归]分析。如果在回归分析中,只包括一个[自变量]和一个[因变量],且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为[多重线性回归]分析。
一元线性回归
回归分析中,如果只包括一个自变量x和一个因变量y,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
那么我们需要做的是致力于找出自变量与因变量之间的连续关系。
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。将会有无数条直线来描述数据集中的线性关系,选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。我们使用最小二乘法来确定最优的直线。
最小二乘法
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
对于观察数据若放在xy直角坐标系中,是一个散点图,假设有一条直线y=a+bx是无数条通过数据集描述的直线,那么要通过最小二乘法确定最佳拟合的a0和a1,将实测值Yi与利用计算值Yj(Yj=a+bXi)差(Yi-Yj)的平方和∑(Yi-Yj)^2最小为“优化判据”。
求解过程:
令:Di =∑(Yi-Yj)^2
把Yj=a+bXi带入φ得到
Di =∑(Yi-a-bXi)^2
当∑(Yi-Yj)^2最小时可用函数 φ 对a、b求偏导数,令这两个偏导数等于零。
整理后对方程组求解
最终解得
由上述过程计算得出最佳拟合一元线性公式。
简例理解最小二乘法
有如下的简单数据集:
通过excel我们可以快速的得出如下的公式:
下图红线的距离为Yi-Yj:
确定y=1.9643x+1为最优的直线的过程是通过实际的每个点到此条直线上对应点的距离(上图红色)的平方和最小,即∑(Yi-Yj)^2最小。
多元线性回归
如果回归分析中包括两个或两个以上的自变量x1,x2...xi,且因变量y和自变量x1,x2...xi之间是线性关系,则称为多元线性回归分析。
多元线性回归可以写作如下方式:
Y=b0+b1x1+…+bkxk+e
其中,b0为常数项,b1,b2…bk为回归系数,b1为X1,X2…Xk固定时,x1每增加一个单位对y的效应,即x1对y的偏回归系数;同理b2为X1,X2…Xk固定时,x2每增加一个单位对y的效应,即,x2对y的偏回归系数,等。
建立多元线性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变量的选择,其准则是:
(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;
(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;
(3)自变量之间应具有一定的互斥性,即自变量之间的相关程度不应高于自变量与因变量之因的相关程度;
(4)自变量应具有完整的统计数据,其预测值容易确定。
多元性回归模型的参数估计,同一元线性回归方程一样,也是在要求误差平方和(Σe)为最小的前提下,用最小二乘法求解参数。以二线性回归模型为例,求解回归参数的标准方程组为
解此方程可求得 b0, b1, b2的数值。亦可用下列 矩阵法求得
即
其中第二种的P(Y=1|x)=y。
逻辑回归
逻辑回归,又名逻辑斯谛回归(logistic regression)是经典分类方法。是一个非常经典的二项分类模型,也可以扩展为多项分类模型。属于对数线性模型。
逻辑回归就是把 线性回归的y 变成了 y的衍生物,是一种 y的广义理解。
我们将线性回归的公式的权值向量(系数)和输入向量(自变量)加以扩充,记做w(欧米伽)和x,即w=(w1,w2...wn,b)的向量,x=(x1,x2...xn,1)的向量,即z=wx,这里我们使用z来代替原本的y以便于区分新的y。那么我们对z做一次衍生,y=f(z)。由此可知z=wx是普通的线性关系,而z到y是一种代数关系。
对预测值的对数函数,需要满足单调可微的性质,且方便进行二项分类,于是选取了S形曲线Sigmoid函数: f(s) = 1 / (1 + exp(-s)), s 取值范围是整个实数域, f(x) 单调递增,0 < f(x) < 1。
Sigmoid 函数在有个很漂亮的“S”形,如下图所示(引自维基百科):
此时将连续性的z,z的范围在(-∞, +∞),变成的连续性的y,y的范围在(0, 1)。
第一种正推思想:
通过Sigmoid 函数衍生出:
y=1/(1+exp(-z))
那么:
exp(-z)=(1/y) - 1
对两方取ln:
-z=ln((1-y)/y)
于是得出:
z=ln(y/(1-y))
带入公式z=wx可得:
ln(y/(1-y))=wx
此时,我们找到了x与y之间的关系。
第二种反证思想:
逻辑斯蒂回归模型是如下的条件概率分布:
一件事情发生的几率为该事件发生的概率与不发生的概率的比值,如果发生的概率为p,那么几率表示为p/1-p。该事件的对数几率为:
综合上述两种公式可得:
逻辑回归的思想应用
y的范围在(0, 1),我们可以将其想象成一种概率,计算出的y可以想象成是这个分类的概率,通过数据集中的x和Y(结果为0或1),求得w向量,对于预测值的新的x,根据已有的w计算y(概率),通过业务场景界定y的大小来判断是否为此分类。
同理,在多类分类问题中,对于多类分类问题,可以将其看做成二类分类问题:保留其中的一类,剩下的作为另一类。对于每一个类 i 训练一个逻辑回归模型的分类器,并且预测y = i时的概率;对于一个新的输入变量x, 分别对每一个类进行预测,取概率最大的那个类作为分类结果。