做有意思的题是要付出代价的,代价就是死活做不出来。
一、题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
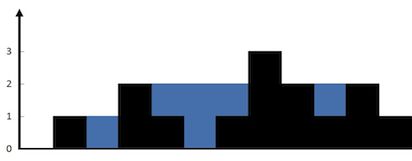
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 1:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
二、我的答案
思路1
前段时间有在看一个俄罗斯方块的代码,所以第一个思路是从下到上一层一层计算,先把数组中所有的数-1,然后去掉数组两端的-1,再统计数组中-1的个数,即为本层接的雨水。这种暴力解法应该是可行的,我并没有把思路落到纸上,各位感兴趣可以试一下。
思路2
接雨水嘛,两边比中间高就能接到,那么我只需要求出所有比左右两边高的点,他们两两组合就成一个可以接到水的坑,以原题中的示例1为例,下标为1,3,7,10的点就是我们所求。代码如下
/**
* @param {number[]} height
* @return {number}
*/
var trap = function(height) {
function fillister (arr) {
let result = 0
let baseLine = arr[0] <= arr[arr.length - 1] ? arr[0] : arr[arr.length - 1]
let difference
for(let i = 0; i < arr.length; i++) {
difference = baseLine - arr[i]
difference > 0 ? result += difference : null
}
return result
}
let result = 0
let bigger, smaller, the_dot
for(let begin = 0; begin < height.length; begin++) {
bigger = (height[begin - 1] || 0) < height[begin]
smaller = (height[begin + 1] || 0) < height[begin]
if (smaller && bigger) {
if (the_dot !== undefined) {
result += fillister(height.slice(the_dot, begin + 1))
}
the_dot = begin
}
}
return result
}; 遍历参数数组height,只要符合条件,且不是第一个符合条件的点,就计算该点与之前点之间的积水。提交,答案错误。出错的测试用例为[5,1,2,1,5]。
原来按照上述思路,只计算了[5,1,2]和[2,1,5]两个小水洼,但是[5,1,2,1,5]本身就是个大水洼。意识到计算目标点的函数需要递归。
根据这个想法,我进行了大量的编码,因为这个递归调用的边界情况比较麻烦,而且越写越怀疑自己的思路,我始终觉得优秀的题解应该是简单的。这里只放出其中对我产生启发的一个片段。
function noNeedToCall (arr) {
let max = Math.max.apply(null, arr)
let maxIndex = arr.indexOf(max)
for(let i = 0, len = arr.length - 1; i < len; i++){
if(i < maxIndex) {
if(arr[i] > arr[i + 1]) return false
} else {
if(arr[i] < arr[i + 1]) return false
}
}
return true
} 上面这段代码的作用在于递归函数调用的最后,判断是否需要继续递归。如果在最大值左边的数组是递增或持平,在最大值右边的数组是递减或持平的就不需要递归,否则继续调用。也就是说最后求出来是以最大值为界,左边一个水洼,右边一个水洼(杠精:“[2,1,3,1,4,1,2]这个例子中最大值4左边有两个水洼,垃圾博主”,)左边一个水洼集,右边一个水洼集。
思路3
虽然左右两个水洼,但是决定他们范围的两个点中的最大值都肯定都是整个数组的最大值,也就是说决定他们积水量的值也就是较小值是存在于左右两边的,那我为什么要各种调用各种递归,直接分左右两侧共循环一遍数组就好了。上代码
/**
* @param {number[]} height
* @return {number}
*/
var trap = function(height) {
const max = Math.max.apply(null, height)
const maxIndex = height.indexOf(max)
let i = 0, temp = 0, result = 0
for (i = 0; i < maxIndex; i++) {
if (height[i] >= temp) {
temp = height[i]
} else {
result += temp - height[i]
}
}
temp = 0
for (i = height.length - 1; i > maxIndex; i--) {
if (height[i] >= temp) {
temp = height[i]
} else {
result += temp - height[i]
}
}
return result
};三、优秀答案
/**
* @param {number[]} height
* @return {number}
*/
var trap = function(height) {
if (!height || !height.length) {
return 0;
}
let maxLeftWall = 0;
let maxRightWall = 0;
let water = 0;
let i = 0;
let j = height.length - 1;
while (i < j) {
if (height[i] < height[j]) {
if (height[i] >= maxLeftWall) {
maxLeftWall = height[i];
} else {
water += maxLeftWall - height[i];
}
i++;
} else {
if (height[j] >= maxRightWall) {
maxRightWall = height[j];
} else {
water += maxRightWall - height[j];
}
j--;
}
}
return water;
};思路是相似的,不过对于处理最大值的方式不同,代码放这儿就不细说了
四、路漫漫其修远兮
这道题真的难了我好久,从想到求水洼两端的点,到递归调用的处理,到推翻之前的思路左右分别处理。过程中各种测试用例a通过测试用例b不通过,跟着debugger一点点看然后改然后测试用例b通过测试用例a又不通过。
最后思路迸发出来写出来提交通过,这种感觉真是爽快,就像是穿着新内裤迎接新年来到的早晨一样。