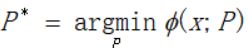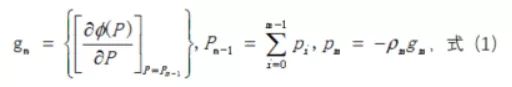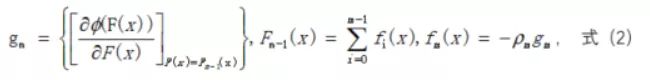主流Gradient Boosting算法对比

本文来自OPPO互联网技术团队，转载请注名作者。同时欢迎关注我们的公众号：OPPO_tech，与你分享OPPO前沿互联网技术及活动。

Gradient Boosting（梯度提升）是一种解决机器学习中分类和回归任务的技术。跟其他Boosting家族成员一样，其预测模型也是由一系列弱预测模型组成的。

近些年来XGBoost、LightGBM以及CatBoost在Kaggle等竞赛中大放异彩，充分证明了Gradient Boosting技术的实用性，所以我们有必要尝试将此技术用于用户兴趣标签的生产中。

本文对当前主流的Gradient Boosting算法做了调研，并从以下几个方面去介绍该技术：第一节先介绍Boosting相关知识，然后引入GBM框架。第二、三、四节分别介绍了GBDT、XGBoost和LightGBM，第五节通过分类特征引出CatBoost算法，最后一节对全文进行一个简单的总结。

1. Gradient Boosting Machine

1.1 Boosting

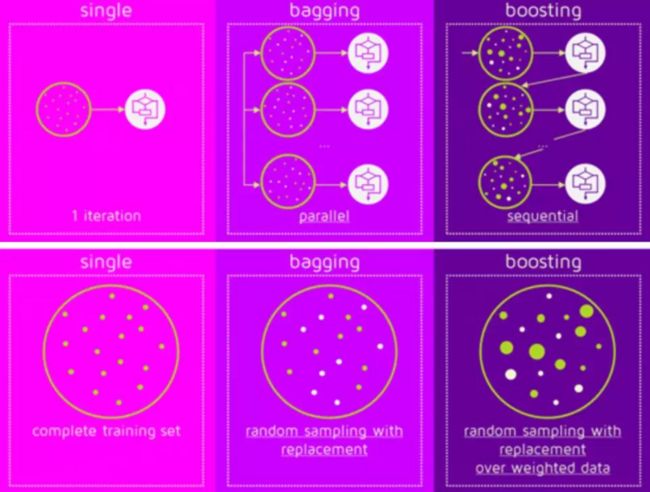
为了对Boosting印象深刻，接下来本文会对比着Bagging进行介绍。如图1所示[1]，Bagging与Boosting都所属Ensemble Learning，但Bagging的各Learner是并行学习，而Boosting则是顺序执行，即Learner处理的是前一个的结果，而且这个结果往往与最初采样的分布不一致。

图1 bagging对比boosting

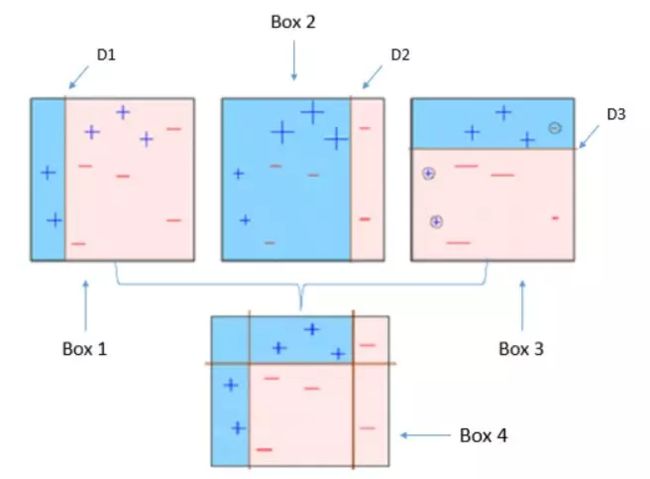
以AdaBoost为例，如图2所示[2]：D1错分了3个正样本，D2训练时会把错分的样本权重增大，D3又把D2分错的负样本权重增大再训练，最后把三个基学习器加权平均（各基学习器间也有权重）得到一个区分能力不错的模型。

图2 AdaBoost：Box1~Box3为按顺序执行的3个Learner，D1~D3分别为各个Box的决策边界，“+ -”表示正负样本，Box4综合了基学习器的决策边界，能很好地区分正负样本

1.2 Gradient Descent

Gradient Boosting与AdaBoost一样，各基学习器都是按顺序学习，但前者的特别之处在于利用了梯度，即将基学习器与梯度联系了起来。在介绍GBM之前，我们先回顾一下数值优化中的梯度下降算法：

设

其中P表示参数、x表示样本、，我们只需在每个迭代中求出pi即可。

具体方法就是给定一个初始参数p0，然后把p0带入式子然后算出梯度，利用梯度信息更新p0得到p1，依次类推：设梯度为g，m表示第m次迭代，则有公式（1）：

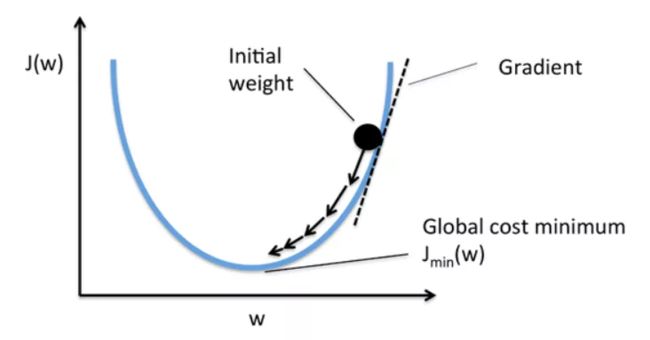
图三用一维参数形象地说明了该算法的原理。

图3 梯度下降法：w沿着负梯度方向更新

可能细心的你已经发现数值优化与Boosting之间的相似之处：

加法模型
顺序执行，即当前环节必须基于前一个环节的结果
数值优化各迭代累加得到最优参数，Boosting各迭代累加起来得到最优函数

既然这么类似，那直接用函数空间替代参数空间，然后直接用梯度下降求解，最优的模型函数岂不是就出来了？是的，GBM的思想就是这样，但在梯度这块儿还需要做更多的考虑，下文将详细介绍GBM。

1.3 Gradient Boosting Machine

前面讲到用函数空间替代参数空间，即用函数F(x)代替（1）式中的参数P，如式（2）所示：

一切看似顺理成章，模型呼之欲出，但别忘了这里的梯度是真实的梯度，即需要知道全集才能算出的梯度，而现实中我们往往是得不到全集的，甚至不知道全集的分布，所以拿有限的样本直接套用式（2）得到的模型其泛化能力令人堪忧。

好在Friedman提出了Gradient Boosting Machine框架：在每个迭代中用有限样本训练基学习器去拟合真实梯度，很好的解决了泛化问题，如图4所示[3]。

图4 Gradient Boosting Machine通用框架。L表示损失函数，F表示模型参数，y表示样本梯度，hx表示基学习器，α为hx参数，ρ表示在线性搜索时的最优参数

图4只给出了一个整体框架，不同的损失函数、不同的基学习器又可衍生出不同的算法，例如选择平方损失函数，则可得图5公式：梯度等价为当前模型预测值与真实值的差（亦称残差），且β=ρ 。

图5 平方损失函数下的GBM

2. GBDT

当GBM中的基学习器为回归树[4]时（拟合的梯度应视为连续值，所以使用回归树），就是经典的GBDT算法。

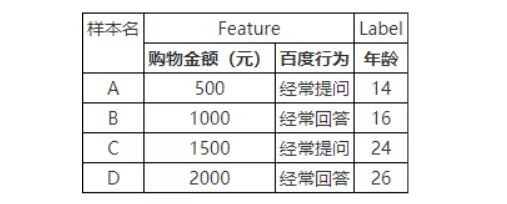
关于公式的转换和其他详情请参考文献4，本文不再赘述，接下来我们使用例子来更直观的感受GBDT的原理：假设我们的任务是预测年龄——即回归任务，所以选择平方损失函数，现在有A、B、C、D四个人，其年龄分别为14、16、24、26岁，特征有购物金额和回答问题行为。

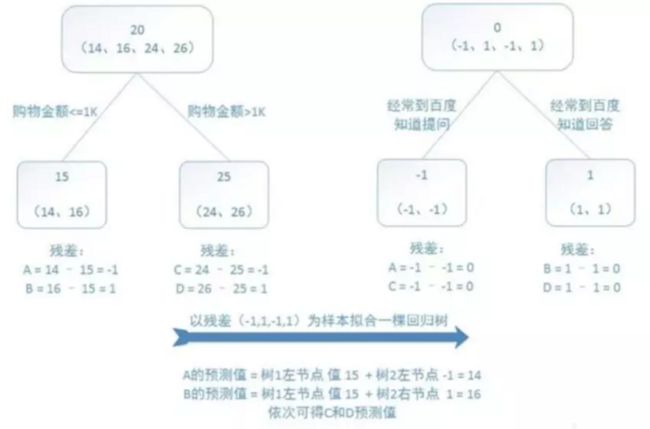
如图6所示，每棵树都会选择一个最佳的特征及其最佳的分裂点；后一颗树的学习样本是前一颗树的残差（亦称残差树），当残差为0时结束训练。

图6 平方损失函数下的GBDT例子

以上的例子很完美，决策树的易过拟合、寻找分裂点付出的高昂时间代价等缺点都没有体现出来。对于过拟合除了决策树的一些手段外[5]，GBM也采取了以下措施：

设置最大迭代数（maxIter）：原因是迭代次数越多，模型越容易过拟合。
增加收缩因子（学习率）：

式中通过学习率v来控制达到收敛的迭代次数，而且可减小后面的树对模型的影响。

SGB（Stochastic Gradient Boosting）：每次迭代从全量数据中抽样（无放回）后学习，此方式既减少了计算量，也有效防止过拟合，一举两得。

对于寻找最佳分裂点的问题，我们先来看一下为什么它如此耗时：如图7所示，首先我们需要对每个特征对应的取值进行预排序，然后把这些值当作分裂点一个个地去计算impurity（不纯度，回归树使用平方误差来表示）来确定最优点，很显然这种方式只适合小数据量和特征维度比较低的场景下。

所以如何改进寻找最优分裂点算法是GBDT的一大课题，本文接下来要介绍的XGBoost、LightGBM也是在这一块做了大量工作。

图7 精确算法（Exact Greedy Algorithms）——先对各特征的取值预排序，再遍历阈值来确定最佳分裂点。图中Impurity采用方差，最佳分裂点的标准是左右child的impurity的和最小。当特征数增多、特征中的取值范围变广、又或者是树的深度变深，则训练一颗树的时间将会变的非常慢

GBDT先告一段落，我们再总结一下它的要点：

使用回归树作为基学习器
回归树的任务就是去拟合梯度，但树节点分裂过程采用的是回归树的准则---平方误差
寻找最优分裂点速度慢，且容易过拟合

3. XGBoost

XGBoost的出现让GBDT真正可以大规模的应用起来：XGBoost的提供了一个Scalable End-to-End 的Tree Boosting系统。

它不仅将正则项引入到损失函数中，也定义了一种树节点分裂的准则——使用1、2阶梯度来决定最优的分裂点，该方法不仅被工程实践证明有效，而且为后面的做差加速奠定了基础。

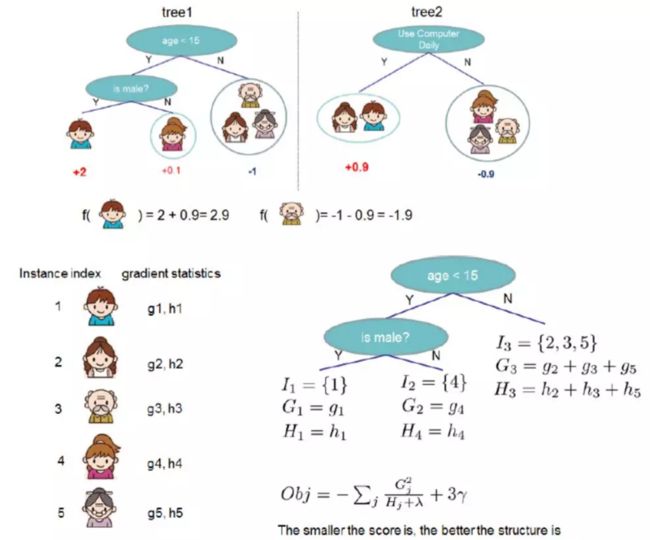
如图8所示，将正则项泰勒级数二阶展开后解出一颗树的“结构分数”(Structure Score)[6]，该分数与当前节点的所有样本的“梯度和”直接相关，若使用直方图叶子节点只需算一个child的，另一个直接用父节点减去当前child就可得到。

不仅如此，XGBoost对图7中的精确算法也做了改进——分位近似算法，该算法不需要将特征中所有值都拿来尝试做分裂点，而是只取分位数的值。以上所述的具体推导公式请见文献6，本文不再赘述，接下来会把XGBoost的主要贡献列出来作为总结：

将正则项引入损失函数，并解析出用于指导树分裂的“结构分数”，该“结构分数”在直方图中可实现做差加速
寻找最优分裂点时的分位近似算法，减少了阈值的个数
列抽样（特征抽样），借鉴随机森林列抽样的方法减少过拟合
支持稀疏数据，树节点分裂时加入默认方向应对些缺失的值
采用Block结构来减少排序时间，并且对cache miss进行了优化

图8 加入正则项后的分裂准则，g为梯度，h为二阶梯度

4. LightGBM

LightGBM在XGBoost的基础上，针对大数据和超高维进行了优化，其具体措施有：

使用特征直方图，即将特征所属的值进行分箱
GOSS（Gradient-based One-Side Sampling）：根据梯度权重采样
EFB（Exclusive Feature Bunding）：特征捆绑

关于直方图很好理解——就是分桶离散化，先把样本按特征值正排序，然后按照策略确定样本与桶的关系（一般策略有等距和等频[7]），特征的取值范围将不大于桶的个数。

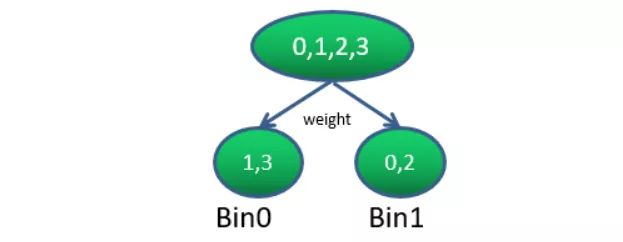
这样做的好处多多：假设特征F有n个值，最大桶数设置为k且k<

如图9所示，直方图由两个要素构成：桶中的样本总数和桶中的所有样本梯度和，以weight为例，我们采用等距离散法将weight的值分到两个桶里——Bin0={1,3}，Bin1={0,2}，图中公式表示的是lightGBM寻找最优分裂点时所用的度量（with GOSS），除了超参它完全由1阶梯度构成，所以我们只用计算左孩子节点的1阶梯度和，右孩子节点梯度和=父节点梯度和-左孩子节点梯度和，以上称之为直方图做差加速。

当然，当我们把2阶梯度也保存起来后，xgboost也能实现直方图做差加速的（参照图8公式）。

图9 直方图结构以及直方图做差加速原理

GOSS实际上就是一种权重采样方法。虽然GBDT所有样本权重都是一致的，但是各样本对应的梯度却是大小不一，所以可以认为样本梯度越大该样本就越重要，GOSS就通过设定一个梯度阈值，且大于该阈值的样本统统都要，而其他的样本则按比例随机抽样。

GOSS虽然减少了训练的样本量，但实际项目中的特征维度一般都很高，所以能否从减少特征个数来优化？

首先应该认识到实际项目中的超高维往往是独热编码导致的，也就是说特征空间是大而稀疏的，已知在稀疏空间中，许多特征之间又是相互互斥的（例如独热编码后的性别特征，不可能同时为1），所以我们可以将这些互斥的特征捆绑在一起，至于具体怎样去捆绑，EFB已经给出了答案。

如图10所示：我们将特征以及特征之间的关系构建出一个图，其顶点为特征，边表示冲突（冲突可以理解为两个特征至少在某个样本中存在同时不为0的情况），但确定图最小颜色数是一个NP-hard，所以图10中是一种理想的情景，实际上EFB给出的贪心算法如图11所示[8]：图的边带有表示冲突程度的权重，设定阈值γ，若冲突程度小于γ则将该特征捆绑一起，以此类推直到本次捆绑结束，下一次捆绑重复上述步骤。

图10 利用特征稀疏性和图着色原理（理想情景）来实现特征捆绑

图11 贪心捆绑算法

5. CatBoost

CatBoost专门对分类特征进行了优化，因为我们用的是二元回归树，所以分类特征是无法直接使用的，目前对分类特征有两种处理方法：

独热编码
标签编码

其中独热编码在我们标签项目中用得比较多，而spark ML中的GBDT默认使用的是标签编码——即每个类别对应一个bin，然后用bin的中心（分类任务中为统计label=1的个数，训练过程中进行）作为该类编码，但是当某类对应的样本量很少时，标签编码容易产生过拟合。

顺便再说一下，目前maxBin都是预留的8位，即最大只有255个，但实际项目中的特征——如APP类型，可以达到上万个。而对GBDT中分类特征是一个类别对应一个bin，很显然如果我们直接把APP类型特征输入GBDT，那只会有255个APP参与训练（事实上这种情况SparkML是会报错提醒的），这时就需要考虑如何缩小分类特征的范围或采用其他编码方法了。

接下来我们来看CatBoost对分类特征做了哪些改进[9]：

改进标签编码——加入先验值减少低频次特征带来的噪声（回归任务：计算label平均值，分类任务：统计label=1个数），并且每个样本的编码基于排在该样本之前的类别标签的均值。
特征组合——可以利用特征之间的联系。
对抗梯度有偏估计——实现了一些解决梯度有偏估计的方法。

本文只对CatBoost做了简单介绍，感兴趣的读者可参考文献9、10深入了解。

6. 总结

本文最开始跟着Friedman论文思想从Boosting和数值优化一路发散到GBM，随后又将决策树引入进来得到GBDT。GBDT中树只是用来拟合梯度，在节点分裂时还是使用的决策树的impurity作为度量，到后来才把梯度给引入到impurity中称之为“结构分数”，这一点在论文6、8中都有提到，因为结构分仅由梯度（或二阶梯度）构成，所以使用直方图不仅可以增加算法鲁棒性，也能在分裂节点的时候加速。

最后，GBDT既是Gradient Boosting也是Tree Boosting，所以我们要清楚各算法改进的是Gradient Boosting还是Tree Boosting。例如对树寻找最优分裂点算法的优化，实际上是Tree Boosting范畴中的优化，CatBoost中的对抗梯度有偏估计更多的是针对Gradient Boosting的优化。

单从论文中的实验数据来看CatBoost > LightGBM > XGBoost > GBDT，但在生产环境中这个排序就不建议参考了，要选最合适自己数据的算法。