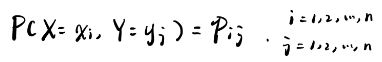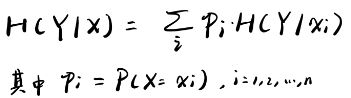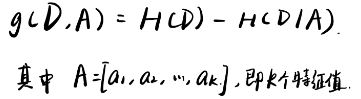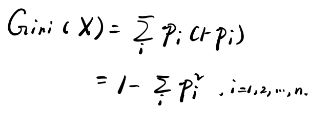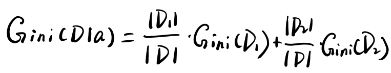机器学习算法复习手册——决策树
本手册整理自机器学习各相关书籍、网络资料、个人的理解与实践。总体编写宗旨:
①一看就懂;
②用20%的文字,涵盖80%的内容。
至于剩下的20%,一般属于比较偏、难的部分,建议自行查询相关书籍资料学习。而只用20%的文字,则代表手册里面几乎没有废话,也只有极少数必要的例子。
下面进入正题。
决策树
决策树是一种基本的分类回归模型。它可以认为是if-then规则的一个集合,或者是特征空间和类空间上的条件概率分布。
优点:模型可读性强,训练速度快。
构建决策树的步骤:
- 特征选择
- 决策树的生成
- 决策树的剪枝
主要算法:ID3(1986年),C4.5(1993年),CART(1984年)
一、特征选择
决策树中的每一个分支是怎么来的呢?比方对贷款违约情况训练一个分类模型,我们有“年龄段”、“是否有房子”、“是否有工作”三个特征。那究竟选择哪个特征呢?
特征选择,就是要选出有“分类效果”的特征。
如何体现“分类效果”?——信息增益,信息增益比,基尼指数
1.信息增益
信息增益,顾名思义,就是信息增加的情况。
何谓信息呢?在信息论中,我们使用“熵”(entropy)来表示事务不确定性的程度,也就是信息量的大小(往往说信息量大,就是指这个事情背后的不确定因素太多了) 。
假设一个随机变量的概率分布为:
则这个随机变量的熵为:
可以看出,熵的大小,跟变量本身的值无关,只跟变量的概率分布有关。
对于随机变量(X,Y),其联合概率分布为:
这个时候,可以定义Y在X的条件下的条件熵:
条件熵的意义就是:在给定了X的信息之后,Y这个随机变量的信息量(不确定性)的大小。
因此,我们可以进一步定义,特征A对数据集D的信息增益(information gain)为g(D|A),它等于D本来的熵,与给定A的条件下的D的条件熵的差值,即:
具体:
从上面的公式很容易理解信息增益的意义:引入了特征A之后,原来数据集D的不确定性减小了多少。
这样,我们就可以方便地计算出每一个特征引入后的信息增益,选择给D带来的信息增益最大的特征,即为最优的特征了。
2.信息增益比
用信息增益作为标准来确定特征的话,存在偏向于特征取值较多的特征,而这样的话很容易造成过拟合。因此,我们引入了信息增益比(information gain ratio)这个指标,对那些特征值过多的特征做一定的“惩罚”:
就是对信息增益除以一个跟A有关的分母,这个分母称为属性A的“固有值”,往往A的特征值越多的话,这个固有值也会越大。
但是,需要注意的是:信息增益比,反过来会对可取值数目较少的特征有偏好。所以也不是信息增益比就一定优于信息增益。
实际上,C4.5算法也不是直接使用信息增益比来进行特征选择,而是先找出信息增益高出平均水平的那些特征,然后再从中挑选信息增益比最高的。
3. 基尼指数
基尼指数跟信息增益的理念不同,它除了要选择最优的特征,还要确定这个特征的最优二值切分点。也就是说,对于每一个特征,我们都只确定一个切分点,将数据集分成两份。而在信息增益(比)的标准中,一个特征有几个值,就会把数据集分成几份。
基尼指数的定义是这样的,对于随机变量X,其基尼指数为:
那么对于一个数据集D,其基尼指数就是:
其中C是类别数。
基尼指数反映了这个数据集的“ 纯度”。基尼指数越小,说明数据集纯度越高。
同样也有条件基尼指数,对于给定特征A后,A中的某一个特征值a将D分成了两部分D1和D2,那么定义咋特征A=a的情况下,D的基尼指数为:
因此,对于一个特征A,我们可以对每一个特征值(划分点)求一个基尼指数,其中最小的那个基尼指数,就对应着这个特征的最佳划分点。
二、决策树的生成
决策树的生成方式,一句话就是:用特征选择指标,从根节点往下一个个节点选择最佳特征,递归地生成决策树。
所以从编程的角度讲,就是一个递归函数:
tree_generation(D,A):
先处理递归终止情况:
1. 如果D所有样本都属于同一类,那么整个D就是一个结点,返回一个叶子节点
2. 如果A是空集,即没有特征供我们选择,则整个D就是一个结点,返回一个叶子节点
再处理其他正常情况:
3. 排除上面两种情况后,选择A中对D的最优特征Ai
4. 如果特征Ai不满足某种条件(不够有区分度,比如信息增益小于某阈值),则D就称为一个叶子节点并返回
4. 如果特征Ai满足某种条件,那么就用Ai对D进行划分,得到若干个子结点,对每个节点,调用tree_generation(Dk,A-Ai)
不同的算法的主要区别在于用什么指标来进行特征选择:
- ID3算法使用信息增益作为指标来选择特征。
- C4.5算法使用信息增益比来选择特征
- CART算法则使用基尼指数
当然,不同的算法还有很多其他细节的不同,例如CART生成的就是二叉树。但是主要的思想就是上面那个递归函数。
三、决策树的剪枝
前面的决策树的生成过程,是完全根据训练集来的,所以会尽可能地去拟合训练集中中的特点,这样形成的树往往会很茂密,分支很多,往往泛化性能就不高。
所以,我们就要使用一个验证集来对生成的树进行“剪枝”处理。
剪枝的基本策略有两种:“预剪枝”和“后剪枝”。
1. 预剪枝
预剪枝,顾名思义,就是不要等到最后再剪,而是在前面有机会剪就剪。
什么时候有机会呢?——当你发现当前对节点的划分不能带来性能的提升时。这个时候就果断把这个小树苗“扼杀在摇篮里”。因此这是一种“自顶向下”的剪枝方法。
比方,对于一个结点,根据训练集的数据,我们发现使用特征A的信息增益(比)最高,所以可以使用A来对该结点进行划分。
但是你担心划分会过拟合,也就是在验证集/测试集上的表现不好。
要怎么判断呢?
- 假设不划分(对应剪枝),那么该结点就是叶子结点了,其类别就是服从大多数的类别。然后,计算一下这个结点在验证集上的准确率α1;
- 假设划分(对应不剪枝),那么该结点就分成了若干个子结点,每个子结点的类别还是按照“服从大多数”的方法来确定。然后,计算一下验证集在各个子结点上的综合的准确率α2;
- 比较一下α1和α2,谁大谁就好。
思路还是很简洁的哈。
预剪枝的方法,使得很多分支,还没出生,就被扼杀,大大减少了决策树训练的时间、计算开销。
但是,这样生成的树,往往很稀疏,存在欠拟合的风险。为啥呢?因为你剪枝的过程“太急”了,可能十分“短视”,有一些节点的划分,可能当前不能提升泛化性能,但是在这个划分的基础上的划分,却可能会有显著的效果提升。这就是短视可能的代价,只追求眼前的利益,可能长远看来确实亏损的。
2.后剪枝
后剪枝,顾名思义,就是事后诸葛亮,先一口气把树使劲生成,然后我再回过头来,一刀一刀地砍。这个时候就只能“自底向上”地砍树了。
思路也很简单:
- 本来整棵树在验证集上的准确率为α1
- 对于一个节点的划分,如果把分支都砍掉,那么就退化成一个结点。使用“服从大多数”法则,确定其类别,计算整棵树在验证集上的准确率α2;
- 比较一下α1和α2,谁大谁就好。
后剪枝明显会比预剪枝的泛化性能更好,欠拟合风险也更低。但是这个方法,需要等树完全生成,所以总体时间开销也比较大。
x、关于决策树的其他
其他细节包括:
- 如何处理连续值
- 如何处理缺失值
- 决策树的分类边界
- ......
这些细节问题建议参考周志华的西瓜书,这里不再赘述。
当然,Talk is cheap, show me the code. 后面的文章我会展示如何用python实现一个简单的决策树模型的思路和代码。
本文参考资料:
1.李航, 《统计学习方法》
2.周志华,《机器学习》