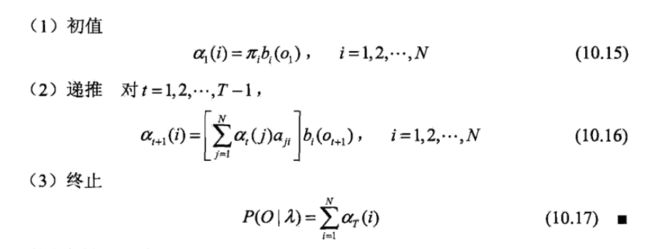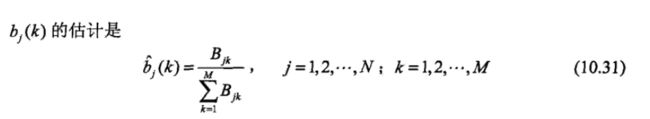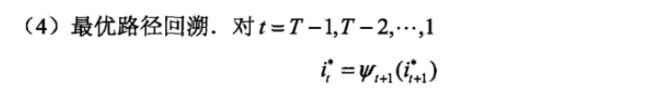前言
最近一直在看机器学习算法模型,但是总是在各种原理以及推导中迷失,感觉自己理解了,但是放下书本却又不知所以然,这种“差不多理解了”现象相信也会困扰很多初学者,于是我就想,能不能有一种方式,简单,通俗,易懂,印象深刻的为大家呈现机器学习这种看上去很“深奥”的知识。
恰巧本周组内小伙伴分享“自然语言处理-中文分词的一些常用方法”,分享过程中两件事情使我印象深刻,第一:很多知识点,总是讲到结果就结束了,没有讲为什么我们需要这样做,比如,讲到基于规则或词典的分词方法时,正向最大匹配法开始使用5个字符进行匹配,如果没有匹配上,则从最后截取一位丢掉,剩下四个字符继续匹配,依次类推。但是,为什么设定5个字符,而不是6个,7个呢?第二:讲到基于统计的分词方法时,隐马尔可夫模型被提到了重点上,但是如何使用隐马尔可夫进行分词,以及隐马尔可夫怎么应用到其他场景,我觉得这是一个模型的重点,模型的思想固然重要,但是怎么讲具体场景抽象到模型上,似乎更为重要,对于一个不是专门搞算法的人来讲。
恰好自己之前看了部分HMM的原理,被同事一讲,豁然开朗,所以准备用自己的理解将HMM讲的更加直观一点。
隐马尔可夫(HMM)基本概念
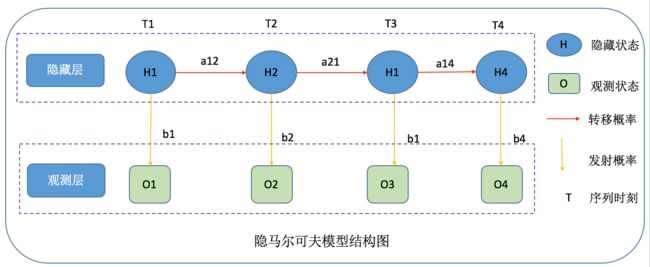
隐马尔可夫模型是一个概率统计模型,主要包含五个部分:
(1)初始概率(PI):用于描述t1(初始)时刻各个隐藏状态发生的可能性
(2)状态序列(H):用于描述隐藏状态的发生序列
(3)观测序列(O):用于描述隐藏状态产生的可观测序列
(4)转移矩阵(A):用于描述各个隐含状态之间转移的概率分布
(5)发射矩阵(B):用于描述隐含状态到观测状态之间的概率分布
一般,一个模型的确定即M=(PI,A,B)
隐马尔可夫(HMM)模型的假设前提
HMM模型成立的前提是做了两个基本假设:
(1)齐次马尔可夫性假设:即假设隐藏的马尔可夫链在任一时刻t的状态只依赖于前一个时刻的状态,与其他状态和观测无关,也与t时刻无关。
(2)观测独立性假设:即任意时刻的观测状态只依赖于该时刻的马尔可夫链状态(隐藏状态),与其他观测状态无关。
隐马尔可夫(HMM)能做什么
在HMM中有三类典型问题:
(1)概率计算问题:已知模型参数M=(PI,A,B),计算某一个给定的观测状态序列(O)的概率,即P(O|M)
(2)解码问题:已知可观测状态序列(O)和模型参数M=(PI,A,B),找到一个最有可能的隐藏状态序列(H),即P(H|O,M)
(3)学习问题:已知可观测状态序列集(O),找到一个最可能的HMM模型(模型各种参数(A,B),使用最大似然估计的方法)
解决以上三类问题,通常我们会有对应的方法来解决:
(1)概率计算问题:直接计算方法(概念可行但计算不可行),前向算法,后向算法
(2)解码问题:近似算法与维特比算法(Viterbi)
(3)学习问题:监督学习算法(训练数据包含观测序列和对应的状态序列),非监督学习算法(Baum-Welch算法即EM算法)
隐马尔可夫应用实例
隐马尔可夫模型应用的一个难点就是如何将问题进行抽象,映射到模型的几个元素上,接下来我将几个常见的博客中的问题进行一下简单抽象。
(1)天气预测问题
观测状态:去公园,在家,去购物
隐藏状态:晴天,雨天,多云
转移概率:晴天到雨天概率,晴天到多云概率。。。。
发射概率:晴天去公园概率,晴天在家概率。。。。。
最终,通过去观察一个人的事件来预测最近几天的天气序列。
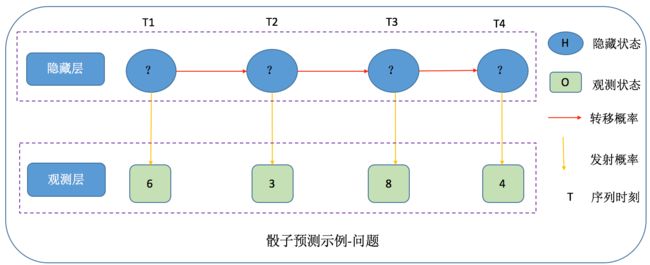
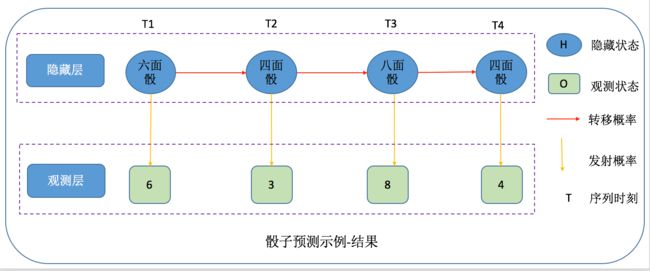
(2)骰子作弊问题
观测状态:骰子掷出来的观测值(1,2,3,4.。。。。)
隐藏状态:使用的骰子类型(八面骰,六面骰。。。。)
转移概率:八面骰到六面骰概率,六面骰到四面骰概率。。。。
发射概率:八面骰掷出1的概率,八面骰掷出2的概率,六面骰掷出2的概率。。。。。
最终,通过去观察一串掷出的骰子序列来预测使用的骰子类型序列。
(3)中文分词问题
观测状态:中文字(我,是。。。。)
隐藏状态:中文状态,B(一个词的开始),M(一个词的中间),E(一个词的结尾),S(单独一个词)
转移概率:开始词到中间词的概率,单字到开始词的概率。。。。
发射概率:开始词到我的概率,开始词到是的概率。。。。。
最终,通过去观察一个中文序列来预测每个字的状态,最后通过状态就可以将词分割出来。
(4)词性标注问题
观测状态:中文词(我,是,男人。。。)
隐藏状态:词性(动词,名词。。。)
转移概率:动词到名词的概率,名词到动词的概率。。。。
发射概率:动态到我的概率,名词词到我的概率。。。。。
最终,通过去观察一个中文词序列来预测每个词的状态,即每个词是什么词性。
ps:以上示例的前提是模型参数已经训练出来,直接进行预测。其实隐马尔可夫模型要解决的三个问题是有内在关联的。即
(1)在不知道模型参数前提下,需要解决学习问题,即通过训练数据,确定模型参数,训练出来模型
(2)在模型通过学习问题学习出来后(或者已知参数,一般教程使用,实际应用不现实),在进行概率计算或者上面示例的预测(解码)
分割线
如果只是想使用隐马尔可夫模型解决实际应用问题,那么上面的内容应该可以满足业务需求的。可以不用向下看了,因为目前很多框架对于模型的集成已经很成熟了,以上内容足够支撑你做一个合格的调参侠了。
如果想对模型的原理进行了解,请跟我来,接下来将分别针对HMM解决的三个问题进行原理分析。
概率计算问题
前向算法:
后向算法
学习问题
(1)训练样本中包含观测状态和对应的状态序列
a.转移概率
b.发射概率
c.初始状态矩阵
根据训练样本的初始值频数计算概率
(2)Baum-Welch算法(EM算法)
后面在EM算法那一篇博客进行讲解
预测(标注)问题
(1)近似算法
但是近似算法的缺点是不能保证预测的状态序列整体是最有可能出现的序列,因为上述方法得到的状态序列中可能存在转移概率为0的相邻状态。
(2)维特比算法
维特比算法实际是使用动态规划解决HMM预测问题。
参考文献
(1)http://www.52nlp.cn/tag/隐马尔可夫模型