普林斯顿《算法》笔记 （一）

官方网站 官方代码

第一章 基础

1.1 基础编程模型

1.1节的内容主要为介绍Java的基本语法以及书中会用到的库。

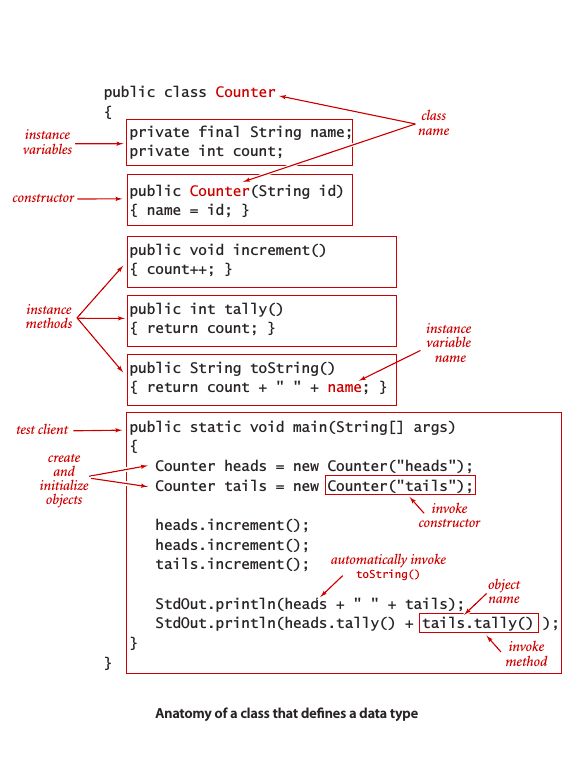
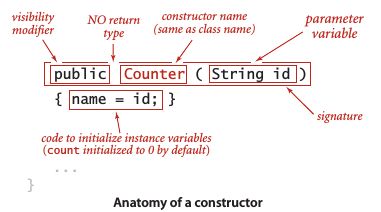
下图为一个Java程序示例和相应的注解：

本书用到的几种基本语法：

1. 初始数据类型 (primitive data tyoes)：整型 (int)，浮点型 (double)，布尔型 (boolean)，字符型 (char)以及组合起来的表达式。
2. 语句 (statements)：声明 (declarations)，赋值 (assignments)，条件 (conditionals)，循环 (loops)，调用 (calls)，返回 (returns)。
3. 数组 (arrays)
4. 静态方法 (static methods)：即函数。
5. 字符串 (strings)
6. 标准输入/输出 (input/output)
7. 数据抽象 (data abstraction)

• Java的int为32位，double为64位
• 除int和double以外的其他初始数据类型：
  1. 64位整数 (long)
  2. 16位整数 (short)
  3. 16位字符 (char)
  4. 8位整数 (byte)
  5. 32位单精度实数 (float)

• i++和++i的区别： ++i等价于i = i + 1和i += 1，即先+1，再进行运算；而i++是先运算再+1。下面演示一下：

public class i_test
{
    public static void main(String[] args)
    {
        int i = 0;
        int j = 0;
        System.out.printf("%s: %d%n","++i",++i);
        System.out.printf("%s: %d%n","i++",j++);
    }
}

/**输出：
++i: 1
i++: 0
*/

数组

1. 创建数组

• 长模式：

double[] a;
a = new double[N];
for (int i = 0; i < N; i++)
    a[i] = 0.0

• 短模式

double[] a = new double[N];
int[] a = {1,1,2,3,6}

• 二维数组

double[][] a = new double[M][N];

2. 别名

数组名表示的是整个数组，如果将一个数组变量赋给另外一个变量，则两个变量将会指向同一个数组：

int[] a = new int[N];
a[i] = 1234;
int[] b = a;
b[i] = 5678  // a[i]也变成5678， 不改变原数组的复制方法见下文

3. 几种数组操作

1）找最大值

double max = a[0];
for (int i = 1;i < a.length; i++)
    if (a[i] > max) max = a[i];

2）计算平均值

int N = a.length;
double sum = 0.0;
for (int i = 0; i < N; i++)
    sum += a[i];
double average = sum / N;

3）复制数组

int N = a.length;
double[] b = new double[N];
for (int i = 0; i < N; i++)
    b[i] = a[i];

4）反转数组中元素

int N = a.length;
for (int i = 0; i < N/2; i++)
{
    double temp = a[i];
    a[i] = a[N-i-1];
    a[N-i-1] = temp;
}

5）矩阵乘法

int N = a.length;
double[][] c = new double[N][N];
for (int i = 0; i < N; i++)
    for (int j = 0; j < N; j++)
    {// Compute dot product of row i and  column j
        for (int k = 0; k < N; k++)
            c[i][j] += a[i][k]*b[k][j];
    }

静态方法

典型的静态方法如下图所示：

1. 几种静态方法实现

1）判断是否为素数

public static boolean isPrime(int N)
{
    if (N < 2)  return false;
    for (int N = 2; i*i <= N; i++)
        if (N % i == 0)  return false;
    return true;
}

2）计算调和级数

public static double H(int N)
{
    double sum = 0.0;
    for (int i = 1; i < N; i++)
        sum += 1.0 / i;
    return sum;
}

输入与输出

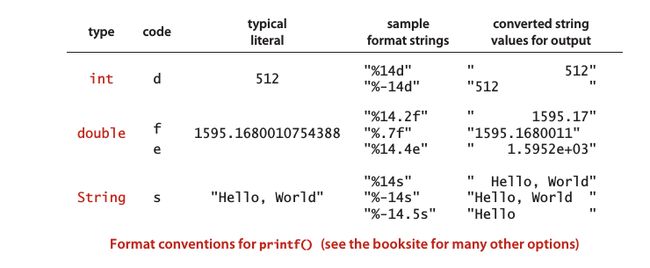
1. 格式化输出：

2. 标准输入

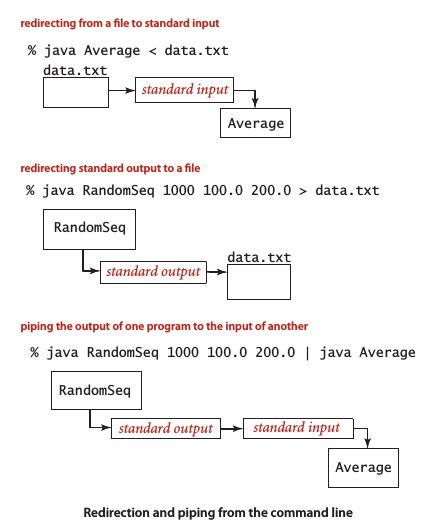
3. 重定向和管道

"<" 表示从文件读取，">"表示写入文件

4. 从文件输入输出

---

1.2 数据抽象

数据类型是指一组值和一组对值的操作的集合，对象是能够存储任意该数据类型的实体，或数据类型的实例。

一个数据类型的例子：

抽象数据类型和静态方法的相同点：

1. 两者的实现均为Java类
2. 实例方法可能接受0个或多个指定类型的参数，在括号中以逗号分隔
3. 可能返回一个指定类型的值，也可能不会（用void表示）

不同点：

1. API中可能会出现名称与类名相同且没有返回值的函数，这些特殊的函数被称为构造函数。在上例中，Counter对象有一个接受一个String参数的构造函数
2. 实例方法不需要static关键字，它们不是静态方法，它们的目的是操作该数据类型中的值
3. 某些实例方法的存在是为了符合Java的习惯，我们将此类方法称为_继承_方法，如上例的toString方法

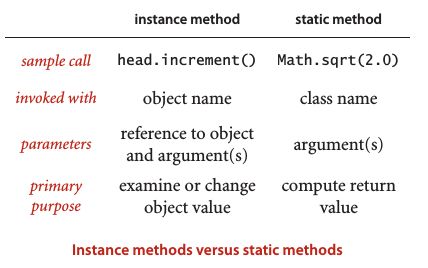
实例方法和静态方法 :

对象

Java中，所有非原始数据类型的值都是对象。对象的三大特性：状态、标识、行为。

引用 (reference) 是访问对象的一种方式，如图所示：

创建对象

要创建 (或实例化) 一个对象，用关键字new并紧跟类名以及 () 来触发它的构造函数。每当用例调用new ()，系统都会：1. 为新对象分配内存空间。 2. 调用构造函数初始化对象中的值。 3. 返回该对象的一个引用。

创建一个对象，并通过声明语句将变量与对象的引用关联起来：

抽象数据类型的实现

组成部分：私有实例变量 (private instance variable)，构造函数 (constructor)，实例方法 (instance method) 和一个测试用例(client) 。

构造函数

每个Java类都至少含有一个构造函数以创建一个对象的标识。一般来说，构造函数的作用是初始化实例变量。如果没有定义构造函数，类将会隐式将所有实例变量初始化为默认值，原始数字类型默认值为0，布尔型为false，引用类型变量为null。

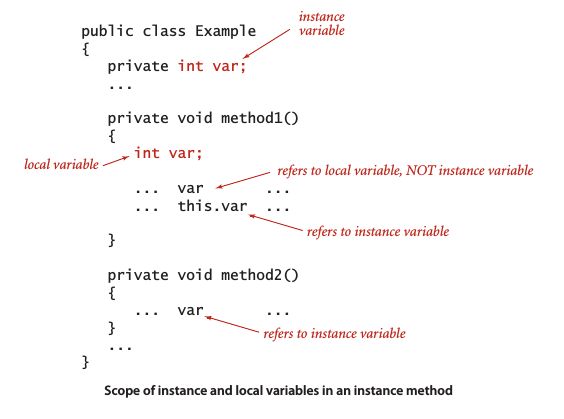
作用域

在方法中调用实例变量，若出现二义性，可使用 this 来区别：

---

1.3 背包、队列和栈

• 本节用到的API：

链表 (Linked List)

链表是一种递归的数据结构，它或者为空 (Null)，或者是指向一个结点 (Node) 的引用，该结点包含一个泛型元素和一个指向另一条链表的引用。

使用嵌套类定义结点的抽象数据类型：

private class Node
{
    Item item;
    Node next;
}

一个Node对象包含两个实例变量，类型分别为Item (参数类型) 和Node，通过new Node () 触发构造函数来创建一个Node类型的对象。调用的对象是一个指向Node对象的引用，它的实例变量均被初始化为null。

构造链表

构造一条含有元素to、be和or的链表，首先为每个元素创建结点：

Node first = new Node();
Node second = new Node();
Node third = new Node();

将每个结点的item域设为所需的值：

first.item = "to";
second.item = "be";
third.item = "or";

然后用next域构造链表：

first.next = second;
second.next = third;

在表头插入结点

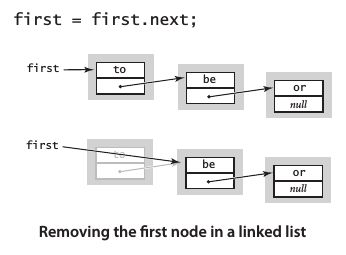
在表头删除节点

将first指向first.next：

在表尾插入节点

链表的遍历

一般数组a[] 的遍历：

for (int i = 0; i < N; i++)
{
// Process a[i].
}

链表的遍历：

for (Node x = first; x != null; x = x.next)
{
// Process x.item.
}

栈 (stack)

栈是一种基于后进先出 (LIFO) 策略的集合类型。

栈的链表实现：

public class Stack
{
    private Node first;
    private int N;
    
    private class Node
    {
        Item item;
        Node next;
    }
    
    public boolean isEmpty() { return first == null; }
    public int size()        { return N; }
    
    public void push(Item item)
    {
        Node oldfirst = first;
        first = new Node();
        first.item = item;
        first.next = oldfirst;
        N++;
    }
    
    public Item pop()
    {
        Item item = first.item;
        first = first.next;
        N--;
        return item;
    }
}

栈测试用例：

public static void main(String[] args)
{ // Create a stack and push/pop strings as directed on StdIn.
    Stack s = new Stack();
    while (!StdIn.isEmpty())
    {
        String item = StdIn.readString();
        if (!item.equals("-"))
        s.push(item);
        else if (!s.isEmpty()) StdOut.print(s.pop() + " ");
    }
    StdOut.println("(" + s.size() + " left on stack)");
}

用链表实现栈的优点：

• 可以处理任意类型的数据
• 所需的空间总与集合的大小成正比
• 操作所需的时间和集合的大小无关

队列 (queues)

队列是一种基于先进先出(FIFO)策略的集合类型。

队列的链表实现：

public class Queue
{
    private Node first;
    private Node last;
    private int N;
    
    private class Node
    {   
        Item item;
        Node next;
    }
    
    public boolean isEmpty() { return first == null; }
    public int size()        { return N; }
    
    public void enqueue(Item item)
    {
        Node oldlast = last;
        last = new Node();
        last.item = item;
        last.next = null;
        if (isEmpty()) first = last;
        else           oldlast.next = last;
        N++;
    }
    
    public Item dequeue()
    {
        Item item = first.item;
        first = first.next;
        if (isEmpty()) last = null;
        N--;
        return item;
    }
}

队列测试用例：

public static void main(String[] args)
{ // Create a queue and enqueue/dequeue strings.
    Queue q = new Queue();
    while (!StdIn.isEmpty())
    {
        String item = StdIn.readString();
        if (!item.equals("-"))
            q.enqueue(item);
        else if (!q.isEmpty()) StdOut.print(q.dequeue() + " ");
    }
    StdOut.println("(" + q.size() + " left on queue)");
}

背包 (bag)

背包是一种不支持从中删除元素的集合数据类型，它的目的是收集元素并迭代遍历所有收集到的元素。使用背包说明元素的处理顺序不重要。

背包的链表实现 + 迭代

import java.util.Iterator;

public class Bag  implements Iterable
{
    private Node first;
    
    private class Node
    {
        Item item;
        Node next;
    }
    
    public void add(Item item)
    {
        Node oldfirst = first;
        first = new Node();
        first.item = item;
        first.next = oldfirst;
    }
    
    public Iterator iterator()
    { return new ListIterator(); }
    
    private class ListIterator implements Iterator
    {
        private Node current = first;
        
        public boolean hasNext()
        { return current != null; }
        
        public void remove() { }
        
        public Item next()
        {
            Item item = current.item;
            current = current.next;
            return item;
        }
    }
}

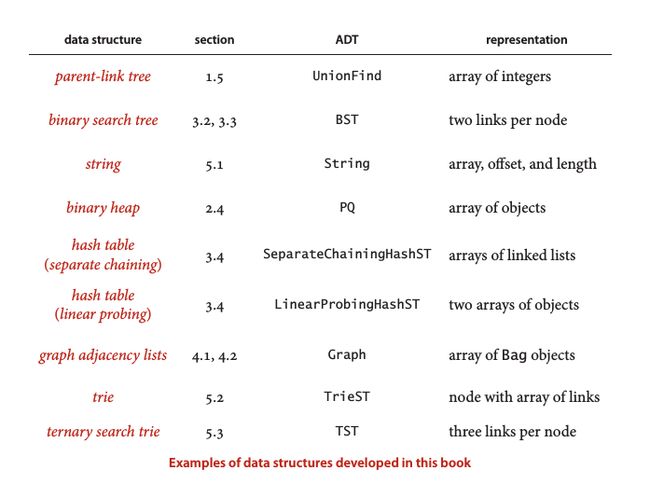
两种基本的数据结构

• 数组，顺序存储 (sequential allocation)
• 链表，链式存储 (linked allocation)

本书所采取的研究新应用的步骤

1. 定义API
2. 根据特定的应用场景开发用例代码
3. 描述一种数据结构 (一组值的表示)，在此基础上定义类的实例变量，该类将实现一种抽象数据类型来满足API中的说明
4. 描述一种算法 (实现一组操作的方式)，在此基础上实现类的实例方法
5. 分析算法的性能特点

---

1.4 算法分析

计时器 —— Stopwatch实现

基于Java中的currentTimeMillis() 方法，该方法能返回以毫秒计数的当前时间。

常见的增长数量级函数

成本模型 (cose model)

本书使用成本模型来评估算法的性质，这个模型定义了算法中的基本操作。例如3-sum问题的成本模型是访问数组元素的次数。

得到运行时间的数学模型，步骤如下：

1. 确定输入模型，定义问题的规模
2. 识别内循环
3. 根据内循环中的操作确定成本模型
4. 对于给定的输入，判断这些操作的执行频率

算法分析的常见函数：

常见增长数量级：

原始数据类型的内存：