前言
距上篇文章已经过了9个月 orz。。趁着期末复习,把博客补一补。。
在前面的文章中介绍了决策树的 ID3,C4.5 算法。我们知道了 ID3 算法是基于各节点的信息增益的大小 \(\operatorname{Gain}(D, a)=\operatorname{Ent}(D)-\sum_{v} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right)\) 进行划分,但是存在偏向选取特征值较多的特征的问题,因此提出了 C4.5 算法,即以信息增益比为标准进行划分 \(\operatorname{Gain}_{-} \operatorname{ratio}(D, a)=\frac{\operatorname{Gain}(D, a)}{I V(a)}\) 其中 \(I V(a)=-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \log \frac{\left|D^{v}\right|}{|D|}\) 。但是,你可能注意到了,ID3 和 C4.5 算法都不能用来做回归问题。这篇文章,将介绍 CART(Classification and Regression Tree) 树的原理,及其实现。
CART 树
基尼系数
与前面介绍的决策树不同,CART 树为二叉树,其划分是基于基尼系数(Gini Index)进行。
先来看看基尼值
\[ \operatorname{Gini}(D)=\sum_{k=1}^{K} \sum_{k^{\prime} \neq k} p_{k} ( 1 - p_{k})=1-\sum_{k=1}^{K} p_{k}^{2} \]
上式从直观上反应了从数据集中任取2个样本,其类别不一致的概率,其值越小,纯度越高。
基尼系数
\[ Gini\_Index(D,a)=\sum_{v=1}^{V}\frac{|D^v|}{|D|}Gini(D^v) \]
划分方式
离散值
也许你已经发现,CART 树在对离散值做划分的时候,若该特征只有两个属性值,那很容易,一边一种就好,但是当属性值大于等于 3 的时候呢?比如 ['青年', '中年', '老年'],这时候应该如何做划分?当然是把所有的方式都遍历一遍啦,存在以下三种情况 [(('青年'), ('中年', '老年')), (('中年'), ('青年', '老年')), (('老年'), ('中年', '青年'))]。到这里我想到了这几个问题:
- 在做数据挖掘竞赛时,大佬们常说做交叉特征能够帮助决策树更好地做划分,是不是因为这种划分方式的原因。
- 这种划分方式是不是有些不太适合具有高基数类别变量的数据?所以有些时候采用对这些变量做 count 等统计特征的时候也会有较大的提升
连续值
之前介绍的都是离散值的处理,那么,当遇到连续值的时候,CART 树又是怎么处理的呢?因为是二叉树,所以肯定是选取一个值,大于这个值的分到一个节点中去,小于的分到另一节点中。
那么,这里就涉及到具体的操作了,一般会在划分时先将这一列特征值进行排序,如果有 N 个样本,那么最多会有 N - 1 种情况,从头到尾遍历,每次选择两个值的中点作为划分点,然后计算基尼系数,最后选择值最小的做划分。
如果你关注算法复杂度的话,会发现 CART 树每次做划分的时候都需要遍历所有情况,速度就会很慢。在 XGBoost 和 LightGBM 中,好像是采用了策略对这一计算进行了加速(挖个坑,后面看 XGBoost 和 LightGBM 的时候补上)。
CART 回归树
用 CART 来做分类问题相信有了 C4.5 与 ID3 的基础,再加上面的介绍,肯定也很容易就知道怎么做了。这里我来讲讲如何用 CART 树来做回归问题。
思考一个问题,树模型并不像线性模型那样,可以算出一个 y 值,那么我们如何确定每个叶子节点的预测值呢?在数学上,回归树可以看作一个分段函数,每个叶子节点确定一个分段区间,叶子节点的输出为函数在该节点上的值,且该值为一个定值。
假设 CART 树 T 将特征空间划分为 |T| 个区域 \(R_i\) ,并且在每个区域对应的值为 \(b_i\) ,对应的假设函数为
\[ h(x)=\sum_{i=1}^{|T|} b_{i} \mathbb{I}\left(x \in R_{i}\right) \]
那么,问题在这里就变成了如何划分区域 \(R_i\) 和如何确定每个区域 \(R_i\) 上对应的值 \(b_i\)。
假设区域 \(R_i\) 已知,那我们可以使用最小平方损失 \(\sum_{x^{(i)} \in R_j}(y^{(i)}-h(x^{i}))^2 = \sum_{x^{(i)} \in R_j}(y^{(i)}-b_j)^2\) ,来求对应的 \(b_j\) ,显然有 \(b_j=avg(y^{(i)}|x^{(i)} \in R_j)\) 。
为了划分区域,可采用启发式的方法,选择第 \(u\) 个属性和对应的值 \(v\),作为划分属性和划分阈值,定义两个区域 \(R_1(u,v)=\{x|x_u\le v\}\) 和 \(R_2=\{x|x_u>v\}\) ,然后通过求解下式寻找最优的划分属性和划分阈值
\[ \min _{u, v}\left[\min _{b_{1}} \sum_{x^{(i)} \in R_{1}(u, v)}\left(y^{(i)}-b_{1}\right)^{2}+\min _{b_{2}} \sum_{x^{(i)} \in R_{2}(u, v)}\left(y^{(i)}-b_{2}\right)^{2}\right] \\ b_i=avg(y^{(i)}|x^{(i)} \in R_i) \]
再对两个区域重复上述划分,直到满足条件停止。
实现
下面又到了愉快的代码时间,这里我只写了分类的情况,回归树只需将里面使用的基尼系数改成上面最小化的式子即可。
def createDataSetIris():
'''
函数:获取鸢尾花数据集,以及预处理
返回:
Data:构建决策树的数据集(因打乱有一定随机性)
Data_test:手动划分的测试集
featrues:特征名列表
labels:标签名列表
'''
labels = ["setosa","versicolor","virginica"]
with open('iris.csv','r') as f:
rawData = np.array(list(csv.reader(f)))
features = np.array(rawData[0,1:-1])
dataSet = np.array(rawData[1:,1:]) #去除序号和特征列
np.random.shuffle(dataSet) #打乱(之前如果不加array()得到的会是引用,rawData会被一并打乱)
data = dataSet[0:,1:]
return rawData[1:,1:], data, features, labels
rawData, data, features, labels = createDataSetIris()
def calcGiniIndex(dataSet):
'''
函数:计算数据集基尼值
参数:dataSet:数据集
返回: Gini值
'''
counts = [] #每个标签在数据集中出现的次数
count = len(dataSet) #数据集长度
for label in labels:
counts.append([d[-1] == label for d in dataSet].count(True))
gini = 0
for value in counts:
gini += (value / count) ** 2
return 1 - gini
def binarySplitDataSet(dataSet, feature, value):
'''
函数:将数据集按特征列的某一取值换分为左右两个子数据集
参数:dataSet:数据集
feature:数据集中某一特征列
value:该特征列中的某个取值
返回:左右子数据集
'''
matLeft = [d for d in dataSet if d[feature] <= value]
matRight = [d for d in dataSet if d[feature] > value]
return matLeft,matRight
def classifyLeaf(dataSet, labels):
'''
函数:求数据集最多的标签,用于结点分类
参数:dataSet:数据集
labels:标签名列表
返回:该标签的index
'''
counts = []
for label in labels:
counts.append([d[-1] == label for d in dataSet].count(True))
return np.argmax(counts) #argmax:使counts取最大值的下标
def chooseBestSplit(dataSet, labels, leafType=classifyLeaf, errType=calcGiniIndex, threshold=(0.01,4)):
'''
函数:利用基尼系数选择最佳划分特征及相应的划分点
参数:dataSet:数据集
leafType:叶结点输出函数(当前实验为分类)
errType:损失函数,选择划分的依据(分类问题用的就是GiniIndex)
threshold: Gini阈值,样本阈值(结点Gini或样本数低于阈值时停止)
返回:bestFeatureIndex:划分特征
bestFeatureValue:最优特征划分点
'''
thresholdErr = threshold[0] #Gini阈值
thresholdSamples = threshold[1] #样本阈值
err = errType(dataSet)
bestErr = np.inf
bestFeatureIndex = 0 #最优特征的index
bestFeatureValue = 0 #最优特征划分点
#当数据中输出值都相等时,返回叶结点(即feature=None,value=结点分类)
if err == 0:
return None, dataSet[0][-1]
#检验数据集的样本数是否小于2倍阈值,若是则不再划分,返回叶结点
if len(dataSet) < 2 * thresholdSamples:
return None, labels[leafType(dataSet, labels)] #dataSet[0][-1]
#尝试所有特征的所有取值,二分数据集,计算err(本实验为Gini),保留bestErr
for i in range(len(dataSet[0]) - 1):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) #第i个特征的可能取值
for value in uniqueVals:
leftSet,rightSet = binarySplitDataSet(dataSet, i, value)
if len(leftSet) < thresholdSamples or len(rightSet) < thresholdSamples:
continue
# print(len(leftSet), len(rightSet))
gini = (len(leftSet) * calcGiniIndex(leftSet) + len(rightSet) * calcGiniIndex(rightSet)) / (len(leftSet) + len(rightSet))
if gini < bestErr:
bestErr = gini
bestFeatureIndex = i
bestFeatureValue = value
#检验Gini阈值,若是则不再划分,返回叶结点
if err - bestErr < thresholdErr:
return None, labels[leafType(dataSet, labels)]
return bestFeatureIndex,bestFeatureValue
def createTree_CART(dataSet, labels, leafType=classifyLeaf, errType=calcGiniIndex, threshold=(0.01,4)):
'''
函数:建立CART树
参数:同上
返回:CART树
'''
feature,value = chooseBestSplit(dataSet, labels, leafType, errType, threshold)
# print(features[feature])
#是叶结点则返回决策分类(chooseBestSplit返回None时表明这里是叶结点)
if feature is None:
return value
#否则创建分支,递归生成子树
# print(feature, value, len(dataSet))
leftSet,rightSet = binarySplitDataSet(dataSet, feature, value)
myTree = {}
myTree[features[feature]] = {}
myTree[features[feature]]['<=' + str(value) + ' contains' + str(len(leftSet))] = createTree_CART(leftSet, np.array(leftSet)[:,-1], leafType, errType,threshold)
myTree[features[feature]]['>' + str(value) + ' contains' + str(len(rightSet))] = createTree_CART(rightSet, np.array(rightSet)[:,-1], leafType, errType,threshold)
return myTree
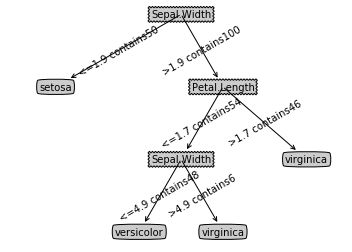
CARTTree = createTree_CART(data, labels, classifyLeaf, calcGiniIndex, (0.01,4))
treePlotter.createPlot(CARTTree)