今天给大家推荐一本自己最近在读,并深受启发,相信对大家也同样有所帮助的书籍——《规模:复杂世界的简单法则》。
本书的作者杰弗里·韦斯特是一名理论物理学家,也是美国圣塔菲研究所(全球复杂性科学研究中心)前所长。在这里主张的研究是跨学科研究,比如物理学家研究生物学、经济学,寻找一种普遍的动力学原理。
初次接触这本书,发现作者是一位物理学家时,我很是担心自己能否有信心和能力读完此书。毕竟高中时期,我可是一名典型的“理科渣”,并曾有过一段从理科转学文科的痛苦经历。
然而,事情并不是我想像的那样。正如这本书的副标题——复杂世界的简单法则那样,作为一名理论物理学家的作者,在向读者解释其研究理论与观点时,同样使用了很多生动,让人容易理解的案例来展开,结合整本书清晰的逻辑,读者便比较容易地理解作者所研究的规模法则在生物学、在城市发展、在公司成长中的体现。
整本书的逻辑清晰、严谨而又简洁。
作者首先提出了自己的研究理论:规模法则,这是万物的尺度。世间的万物,不管是生物体的生命代谢、全球各大城市由小到大的持续发展,以及成千上万的公司由小到大,再由盛而衰的过程,都遵循着规模法则,他们的成长与发展受到其自身规模的促进,同时也受到规模限制,并呈现出一定非线性比例关系,不管是亚线性(受限制)还是超线性(受促进)。
提出了自己的观点之后,作者便利用自己在研究过程中发现的大量的事实、数据、图表等来分别解释并证明规模法则在生物学、城市和公司等社会经济活动中的体现。
比如,在生物学中,有一个著名的代谢率规模法则,又叫克莱伯定律,是生物学家克莱伯阐述的,指的是生物体的代谢率随着体重的约3/4次幂发生变化。
举个例子来说明,比如大象的体现差不多是老鼠的10^4倍,相应的大象的细胞数也是老鼠的10^4倍,但是大象的代谢率(保持大象存活所需的能量)却只是老鼠的10^3倍,并不是10^4倍。意思就是,代谢率随体重或体积的增长并不是线性的,而是非线性的。如果是我们相当然理解的线性增长,那么大象的代谢率应该是老鼠的10^4倍。 正是因为规模法则的这种非线性,使得规模每扩大一倍,代谢率只增长了75%,并不是100%,这便会产生25%的节余。而这,正是大型哺乳动物比小型哺乳动物更加长寿的秘密所在。因为如果一只哺乳动物体重增长一倍,它的心率便会下降25%。这就是规模带来的好处。
这个3/4次幂法则就是一种规模法则的非线性数学法则,具体来说就是亚线性(因为<1,如果>1就是超线性)。有趣的是,这种亚线性增长一方面导致了体形更大的动物寿命更长,一方面又导致了我们最终停止生成,把人类寿命极限定格在125岁左右。当然,具体如何定格就不一一阐述,涉及到作者提出来的网络系统的限制,感兴趣的同学可以去买这本书看。
当然,这一法则还体现在很多生活中的其他现象之中。比如,很多人误认为药特剂量应该随体重变化而呈现线性变化,但是实际上儿童的药物剂量并不是随着体重的增加而按线性比例增加。作者发现,这种增加是遵照非线性的2/3次幂规模法则的。
作者把这种在生物学中所发现的规模法则应用到现代社会经济学的研究之中,发现人类的城市发展与公司成长同样遵照这种非线性法则。
比如为什么我们都喜欢去大城市?
我们都知道,随着城市人口规模的增加,城市的就业机会、经济增长、专利、收入等都会增加,但是是否是随人口增加而呈线性增加呢?
并不是。作者认为城市的发展遵守一个15%法则。城市规模每扩大一倍,其带来的社会互动、经济收入、专利、创新、犯罪、疾病等会增加100%+15%,也就是1.15倍,是一种超线性增长;而城市的物理基础设施、能量使用等只增加了100%-15%,即85%,也就是节约了15%,这是一种亚线性增长。社会资本的超线性创造速度,超过了维护城市的基础设施和能量的亚线性增长速度,导致越来越快的开放式增长。这就是作者认为的,为什么人类城市从几千年发展至今,一直能持续下去的原因。而不像生物有生命结束的时刻,以及后面所讲的公司,有倒闭的时刻。
然而,正是社会经济活动的1.15倍超线性增长,导致作为社会人的我们,生活节奏越来越快,而以后还会更快。
同样的,规模法则也适用于公司的发展。
公司的许多关键指标更像生物体一样呈亚线性比例变化,而不是像城市那样呈超线性变化。
人类的生命拥有极限在于新陈代谢产生的能量,跟不需要维护的细胞的需求。因为人类在新陈代谢过程中,会慢慢出来细胞的磨损。在生命的早期,我们的代谢产生的能量可以说几乎都用于生命的增长,而不是维护;随着年龄的增长,出现磨损的细胞越来越多,并用这种磨损是有累积效应的。因此,代谢产生的能量越来越多地应用于维护细胞,直到有一天跟不上需要维护的需求。这就是为什么我们在生命的早期会发育得更快。
公司亦是如此。公司在早期拥有大量的资本与投入,这种资本投入保证公司快速发展。但是当公司进入一个稳定收效期,拥有一种稳定产生效益的产品或服务之后,越来越多的人力、资本被投入到维护这种增长之中,包括企业的运营、组织架构等越来越广泛。而且,随着市场的变化,这种增长还要大打折扣,因为单独一家公司相对于整体市场扩张的增长情况并不理想。
所以作者认为,那些从倒闭潮中幸免下来的公司,看起来很知名很成熟,但是其增速相当缓慢,处于陷阱和危险之中。总会有一天,这种缓慢的增长赶不上维护这种增长所需的成本,两者之间的差距越来越大,那便到了雪崩的时刻的。
当然,如果有创新的手段和行为,公司是可以重新成长的。这就由此引出了另外一个目前不管是在经济发展,还是在公司管理中都越来越受人重视的——创新。
人类自从有文明以来,便不断地加速跑步前进,而几次工业革命更是让人类越来越快,像是在一个跑步机上不断加速。
作者认为,总会有那么一个时间点的存在,我们的资源、环境等不足以支撑经济的无限发展。因为在这个有限的时间奇点前,不可能有无限供应的能量资源。如下图所示。
我们一直像这个数学公式所表现的一样,在迈向这个奇点。那么阻止这个灾难的发生,则是在奇点到来之前进行干预,重新设定公式的参数。这个干预就是我们经常提及的创新。
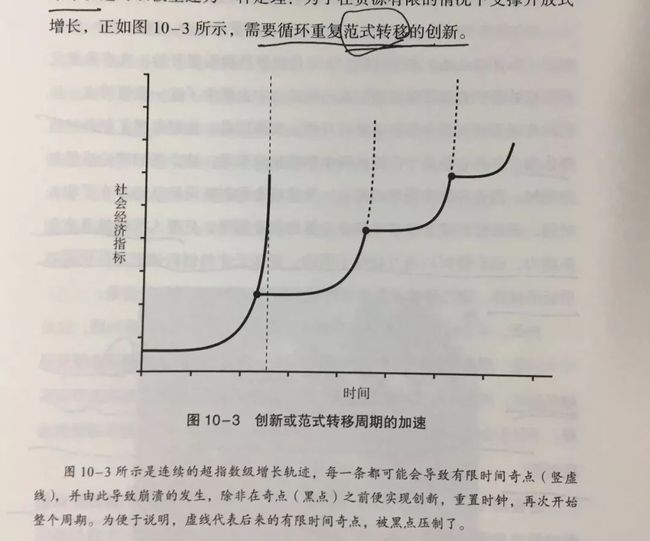
在每一次崩溃到来之前,我们都需要发起新的创新,来改变系统的运行路径,让增长继续,避开到来的奇点。整个连续的过程不断地重复,把可能的崩溃推至人类的聪明才智能够允许的未来。如下图所示。
这就是为什么,越来越多的国家经济增长和企业发展,需要不断的创新。
但是正如上图所示的一样,每个黑点代表一个创新时间段。我们发现连续创新之间的间隔变得越来越短,也就是创新必须以越来越快的节奏实现。
所以作者说,我们不仅仅是生活在不断加速的跑步机上,而且在某个阶段,我们还必须要跟到另一个以更快的速度加速的跑步机上,如此循环。
这像极了神话里的西西弗斯不停歇地把一块巨大的石头推向山顶,而我们比西西弗斯困难得多,因为每一次要以更快的速度向上推。
无论我们多么聪明,发明多少科技,我们永远摆脱不了终极奇点的威胁。
这似乎是一个没有答案的困扰。因此作者在书的最后设想,人类是否能够回到更加“生物化”的阶段,也就是接受某种亚线性变化,而不是现在的超线性增长,把我们引向潜在的无知的灾难。
当然,作者也希望在不远的将来,人类有重大的突破,能提出一个大一统的可持续发展理论。
最后,豌豆再次和大家推荐有时间要读一读这本书,接近500页的页数,却没有一丝废话,信息量很大,书中的很多数学和物理规律均配有精彩的案例演示,对于增加常识也是一种很好的选择。
当然有些内容会有一些难以理解,需要反复阅读和思考才能理解,想一想你的大脑被智能设备绑架了多久,有多久没有转动了,让大脑动起也是一件好事。尤其是要转变我们固有的线性思维,认识到这个世界是一个复杂的系统,在这个复杂的网络系统里,很多事情的发展并不是线性的,而是非线性的缩放!
另外,这本书从宏观角度分析了万物背后的发展规律,对于理解我们的身体、理解经济行为,以及公司的管理与创新同样很有启发。
-END-