一.课程设计题目及要求
(一)课程设计题目
用顺序和二叉链表作存储结构实现二叉排序树:
(1)以回车('\n')为输入结束标志,输入数列L,生成一棵二叉排序树T;
(2)对二叉排序树T作中序遍历,输出结果;
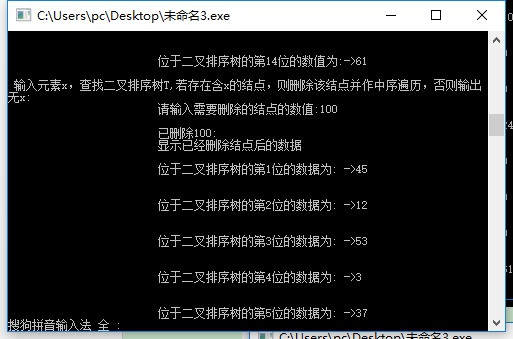
(3)输入元素x,查找二叉排序树T,若存在含x的结点,则删除该结点,并作中序遍历(执行操作2);否则输出信息“无x”。
(二)课程设计要求
在处理题目时,要求从分析题目的需求入手,按设计抽象数据类型、构思算法、通过设计实现抽象
数据类型、编制上机程序和上机调试等若干步骤完成题目,最终写出完整的分析报告。对于稍复杂
的程序设计,要充分利用模块化程序设计方法,自顶向下,逐步细化,在整体思路确定的情况下,
考虑所需模块数,各模块完成功能以及模块之间的数据联系和调用关系。给出主要模块的算法描
述,用流程图或伪代码表示。说明:在设计的过程中,步骤1---步骤4往往是反复进行, 在后续步
骤中发现问题,往往需要从头重新分析、设计。
二.算法思想
(一)二叉排序树的定义
二叉排序树的定义:二叉排序树或者是一棵空树, 或者是一棵具有如下性质的二叉树:
(1)每个结点都有一个作为搜索依据的关键码(key),所有结点的关键码互不相同;
(2)若它的左子树非空,则左子树上所有结点的值均小于根结点的值;
(3)若它的右子树非空,则右子树上所有结点的值均大于根结点的值;
(4)左、右子树本身又各是一棵二叉排序树
(二)二叉排序树的实现
1.建立二叉排序树
建二叉树的结点至少应当包含三个域,分别存放结点的数据data,左子女结点指针leftChild和右子女结点指针rightChild。整个二叉树的链表要有一个表头指针,它指向二叉树的根结点,其作用是当作树的访问点
从空的二叉排序树开始,经过一系列的查找插入操作以后,生成了一棵二叉排序树。
根据二叉排序树的定义,建立一棵二叉排序树的过程是按照待排序序列元素的先后次序,不断动态生成二叉树的结点,逐个插入到二叉树中。若p为根结点指针,b为当前待插入元素,其过程可以描述为:
若为空树(p=NULL),动态生成一个结点,其数据域为当前待插入元素b,左、右指针域为“空”,p指向该结点。若非空树,比较b与根结点数据data(p)
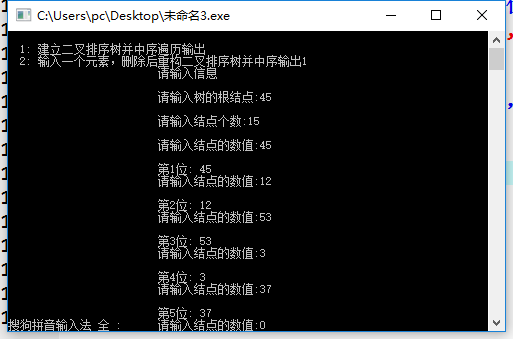
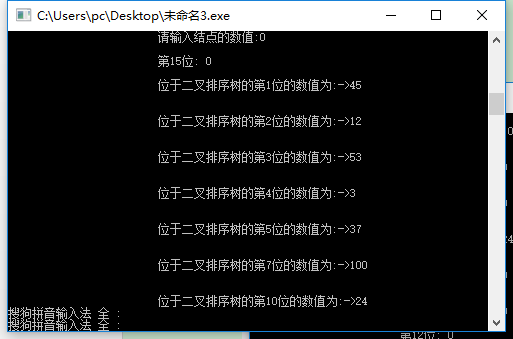
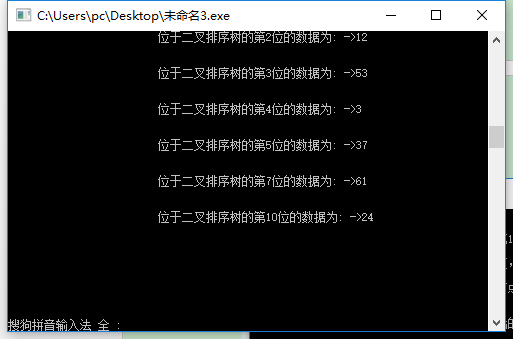
如果b 如果b≥data(p),将b插入右子树中; 左、右子树的插入方式与二叉排序树的插入方式相同。 不断调用上述的插入过程,直到所有待排序序列均排入后,就形成一棵二叉排序树。 由此可见,建立二叉排序树就是多次调用二叉排序树的插入算法。 中序遍历二叉树算法的框架是: 若二叉树为空,则空操作; 否则 中序遍历左子树(L); 访问根结点(V); 中序遍历右子树(R)。 中序遍历二叉树也采用递归函数的方式,先访问左子树,然后访问根结点,最后访问右子树.直至所有的结点都被访问完毕 在二叉排序树上进行查找,是一个从根结点开始,沿某一个分支逐层向下进行比较判等的过程。它 可以是一个递归的过程。假设我们想要在二叉排序树中查找关键码为x的元素,查找过程从根结点 开始。如果根指针为NULL,则查找不成功;否则用给定值x与根结点的关键码进行比较;如果给定 值等于根结点的关键码,则查找成功,返回查找成功的信息,并报告查找到的结点地址。如果给定 值小于根结点的关键码,则继续递归查找根结点的左子树;否则,递归搜索根结点的右子树。 对于二叉排序树,删去树上的一个结点相当于删去有序序列中的一个记录,只要在删除某个结点之 后依旧保持二叉排序树的特性即可。假设在二叉排序树上被删除结点为*p(指向结点的指针是 p),其双亲结点为*f(结点指针为f),且不失一般性,可设*p是*f的左孩子,若*p结点为叶子结 点,即p和l均为空,只需修改其双亲结点指针即可。若*p结点只有左子树或者只有右子树,只要令 左子树或右子树直接成为其双亲结点即可。若左子树和右子树都不为空,令*p的直接前驱替代*p, 然后从二叉排序树中删除它的直接前驱,即可。 程序主要设计了四个功能:首先是创建二叉排序树,完成后出现任务菜单,以数字代码确定,二叉 排序树的中序遍历和查找,删除步骤,最后完成,结束。 #include #include typedef int ElementType; typedef struct TNode *Position; typedef Position BinTree; struct TNode{ ElementType Data; BinTree Left; BinTree Right; }; void PreorderTraversal( BinTree BST ); void InorderTraversal( BinTree BST ); BinTree Insert( BinTree BST, ElementType X); BinTree Delete( BinTree BST, ElementType X); Position Find( BinTree BST, ElementType X); Position FindMin( BinTree BST ); Position FindMax( BinTree BST ); void solve( BinTree BST ); int calculateASL( BinTree BST,double*s,double *j,int i ); int main() { BinTree BST, MinP, MaxP, Tmp; ElementType X; int number,N, i; BST = NULL; scanf("%d", &N); for ( i=0; i scanf("%d", &X); BST = Insert(BST, X); } printf("Preorder:"); PreorderTraversal(BST);printf("\n"); /*MinP = FindMin(BST); MaxP = FindMax(BST); scanf("%d", &N); for( i=0; i scanf("%d", &X); Tmp = Find(BST, X); if (Tmp == NULL) printf("%d is not found\n", X); else { printf("%d is found\n", Tmp->Data); if (Tmp==MinP) printf("%d is the smallest key\n",Tmp->Data); if (Tmp==MaxP) printf("%d is the largest key\n",Tmp->Data); } } scanf("%d", &N); for( i=0; i scanf("%d", &X); BST = Delete(BST, X); }*/ printf("Inorder:"); InorderTraversal(BST);printf("\n"); double s=0,j=0; int k=0; calculateASL(BST,&s,&j,k); printf("ASL=%0.4f\n",s/j); solve(BST); return 0; } void PreorderTraversal( BinTree BST ) { if( BST ) { printf(" %d", BST->Data); PreorderTraversal( BST->Left ); PreorderTraversal( BST->Right ); } } void InorderTraversal( BinTree BST ) { if( BST ) { InorderTraversal( BST->Left ); printf(" %d", BST->Data); InorderTraversal( BST->Right ); } } Position Find( BinTree BST, ElementType X ) { if( !BST ) return NULL; /*查找失败*/ if( X > BST->Data ) { return Find(BST->Right,X );/*在右子树中.继续查找*/ } else if( X < BST->Data ){ return Find( BST->Left,X ); /*在左子树中继续查找*/ } else /* X == BST->Data */ return BST; /*查找成功,返回结点的找到结点的地址*/ } Position FindMin( BinTree BST ) { if(BST){ while(BST->Left){ BST=BST->Left; } } return BST; } Position FindMax( BinTree BST ) { if(BST ){ while( BST->Right ){ BST = BST->Right; }/*沿右分支继续查找,直到最右叶结点*/ } return BST; } BinTree Insert( BinTree BST, ElementType X) { if( !BST ){ /*若原树为空,生成并返回一个结点的二叉搜索树*/ BST = (BinTree)malloc(sizeof(struct TNode)); BST->Data = X; BST->Left = NULL; BST->Right = NULL; } else { /*开始找要插入元素的位置*/ if( X < BST->Data ) BST->Left = Insert( BST->Left, X );/*递归插入左子树*/ elseif( X > BST->Data ) BST->Right = Insert( BST->Right,X ); /*递归插入右子树*/ /* else X已经存在,什么都不做*/ } return BST; } BinTree Delete( BinTree BST, ElementType X) { BinTree head=BST; BinTree t=Find(BST,X); if(!t) { printf("Not Found\n"); return BST; } BinTree m=FindMax(t->Left); if(m) {//左子树处理 t->Data=m->Data; if(t->Left==m)t->Left=m->Left; else { t=t->Left; while(t->Right!=m)t=t->Right; t->Right=m->Left; } }else { m=FindMin(t->Right); if(m) {//左子树为空时 t->Data=m->Data; if(t->Right==m)t->Right=m->Right; else { t=t->Right; while(t->Left!=m)t=t->Left; t->Left=m->Right; } } else { //当其为叶节点时 if(BST==t)return NULL; while(BST) { if(BST->Data>=t->Data){ if(BST->Left==t)BST->Left=NULL; BST=BST->Left; } else { if(BST->Right==t)BST->Right=NULL; BST=BST->Right; } } } } // free(t); return head; } void solve( BinTree BST ) { ElementType X; Position tmp; printf("which element will you delete:"); scanf("%d",&X); tmp = Find( BST,X ); if(tmp ==NULL)printf("thereis not X!\n"); else{ BST = Delete( BST, X ); InorderTraversal(BST); } } int calculateASL(BinTree BST,double *s,double *j,int i) /*计算平均查找长度*/ { if(BST){ i++; *s=*s+i; if(calculateASL(BST->Left,s,j,i)){ (*j)++; if(calculateASL(BST->Right,s,j,i)){ i--; return(1); } } } else return(1); #include"stdio.h" #include"malloc.h" #include"windows.h" #define endflag 999999 #define N 1000 int b[N]; typedef struct { intdata; intother; intflag1; }Link; void Build(Link a[N]) { intw,i,j,k; for(i=0;i<=N;i++){ a[i].flag1=0; a[i].data=0; } printf("\n\t\t\t请输入树的根结点:"); scanf("%d",&a[1].data); a[1].flag1=1; printf("\n\t\t\t请输入结点个数:"); scanf("%d",&k); for(j=1;j<=k;j++){ printf("\n\t\t\t请输入结点的数值:"); scanf("%d",&w); printf("\n\t\t\t第%d位: %d",j,w); a[0].data=w; a[0].flag1=1; i=1; if(a[0].data loop:if(a[2*i].flag1==0){ a[2*i].data=a[0].data; a[2*i].flag1=a[0].flag1; } if(a[2*i].flag1==1){ i=2*i; if(a[0].data if(a[0].data>a[i].data)goto loop1; } } if(a[0].data>a[i].data){ loop1:if(a[2*i+1].flag1==0){ a[2*i+1].data=a[0].data; a[2*i+1].flag1=a[0].flag1; } if(a[2*i+1].flag1==1){ i=2*i+1; if(a[0].data gotoloop; if(a[0].data>a[i].data) gotoloop1; } } } } void Sdel(Link a[N]) { inti,flag=0,q,number=1,j=1; printf("\n\t\t\t请输入需要删除的结点的数值:"); scanf("%d",&q); for(i=1;i<=N;i++) if(a[i].data==q){ a[i].data=0; printf("\n\t\t\t已删除%d: ",q); flag=1; for(i=1;i<=N;i++){ if(a[i].data!=0){ b[j]=a[i].data; j++; number++; } } for(i=1;i<=N;i++){ a[i].flag1=0; a[i].data=0; } a[1].data=b[1]; a[1].flag1=1; for(j=2;j<=number-1;j++){ a[0].data=b[j]; a[0].flag1=1; i=1; if(a[0].data loop:if(a[2*i].flag1==0){ a[2*i].data=a[0].data; a[2*i].flag1=a[0].flag1; } if(a[2*i].flag1==1){ i=2*i; if(a[0].data if(a[0].data>a[i].data)goto loop1; } } if(a[0].data>a[i].data){ loop1:if(a[2*i+1].flag1==0){ a[2*i+1].data=a[0].data; a[2*i+1].flag1=a[0].flag1; } if(a[2*i+1].flag1==1){ i=2*i+1; if(a[0].data if(a[0].data>a[i].data)goto loop1; } } } printf("\n\t\t\t显示已经删除结点后的数据\n"); for(i=1;i if(a[i].data!=0){ printf("\n\t\t\t位于二叉排序树的第%d位的数据为: ",i); printf("->%d\n\n",a[i].data); } } } if(flag==0)printf("\n\n\n\t\t\t不存在该结点,不能删除\n"); } int main() { inti,flag=0,ch=0; Linka[N]; printf("\n1:建立二叉排序树并中序遍历输出"); printf("\n2:输入一个元素,删除后重构二叉排序树并中序输出"); while(ch==ch){ scanf("%d",&ch); switch(ch){ case0:exit(0); case1:printf("\t\t\t请输入信息\n"); Build(a); printf("\n"); for(i=1;i if(a[i].data!=0){ printf("\n\t\t\t位于二叉排序树的第%d位的数值为:",i); printf("->%d\n\n",a[i].data); } } case2:printf("输入元素x,查找二叉排序树T,若存在含x的结点,则删除该结点并作中序遍历,否则输出无x:"); Sdel(a); break; default: printf("无此结点\n"); break; } } return0; } #include #include #include #include using namespace std; typedef struct TreeNode *AvlTree; typedef struct TreeNode *Position; struct TreeNode { int Data; AvlTree Left; AvlTree Right; int Height; }; void PreorderTraversal( AvlTree AVL ) { if( AVL ) { printf("%d ", AVL->Data); PreorderTraversal( AVL->Left ); PreorderTraversal( AVL->Right); } } void InorderTraversal( AvlTree AVL ) { if( AVL ) { InorderTraversal( AVL->Left ); printf("%d ", AVL->Data); InorderTraversal( AVL->Right); } } int calculateASL(AvlTree AVL,double *s,double *j,int i) /*计算平均查找长度*/ { if(AVL){ i++; *s=*s+i; if(calculateASL(AVL->Left,s,j,i)){ (*j)++; if(calculateASL(AVL->Right,s,j,i)){ i--; return(1); } } } else return(1); } AvlTree Insert(int x, AvlTree T);//插入新节点,必要时调整 Position SingleRotateWithLeft(Positiona);//左单旋 Position SingleRotateWithRight(Positionb);//右单旋 Position DoubleRotateWithLeft(Positiona);//左右旋 Position DoubleRotateWithRight(Positionb);//右左旋 int Max(int x1, int x2);//返回两个int中较大的 int Height(Position P);//返回一个节点的高度 int main() { int n, x; AvlTree T = NULL; scanf("%d", &n); for (int i = 0; i < n; i++) { scanf("%d", &x); T = Insert(x, T); } printf("Preorder:"); PreorderTraversal(T);printf("\n"); printf("Inorder:"); InorderTraversal(T);printf("\n"); ///printf("%d\n", T->Data);//打印根节点的值 double s=0,j=0; int k=0; calculateASL(T,&s,&j,k); printf("ASL=%0.4f\n",s/j); return 0; } AvlTree Insert(int x, AvlTree T) { if (T == NULL) { T = (AvlTree)malloc(sizeof(struct TreeNode)); T->Data = x; T->Left = T->Right = NULL; T->Height = 0; } else if (x < T->Data)//向左子树插入 { T->Left = Insert(x, T->Left); if (Height(T->Left) - Height(T->Right) == 2)//需调整 { if (x < T->Left->Data) T = SingleRotateWithLeft(T); else T = DoubleRotateWithLeft(T); } } else if (x > T->Data)//向右子树插入 { T->Right = Insert(x, T->Right); if (Height(T->Right) - Height(T->Left) == 2)//需调整 { if (x >T->Right->Data) T = SingleRotateWithRight(T); else T = DoubleRotateWithRight(T); } } /*else值为x的节点已经存在树中,无需插入*/ /*更新节点高度*/ T->Height = Max(Height(T->Left), Height(T->Right)) + 1; return T; } Position SingleRotateWithLeft(Position a) { Position b = a->Left; a->Left = b->Right; b->Right = a; //更新a, b节点高度 a->Height = Max(Height(a->Left), Height(a->Right)) + 1; b->Height = Max(Height(b->Left), Height(b->Right)) + 1; return b;/*新的根节点*/ } Position SingleRotateWithRight(Position b) { Position a = b->Right; b->Right = a->Left; a->Left = b; //更新a,b节点高度 a->Height = Max(Height(a->Left), Height(a->Right)) + 1; b->Height = Max(Height(b->Left), Height(b->Right)) + 1; return a;/*新的根节点*/ } Position DoubleRotateWithLeft(Position a) { a->Left = SingleRotateWithRight(a->Left); return SingleRotateWithLeft(a); } Position DoubleRotateWithRight(Position b) { b->Right = SingleRotateWithLeft(b->Right); return SingleRotateWithRight(b); } int Max(int x1, int x2) { return (x1 > x2) ? x1 : x2; } int Height(Position P) { if (P == NULL)//空节点高度为-1 return -1; return P->Height; } (1)二叉链表存储(BST): (2)顺序存储(BST): (3)二叉链表存储(AVL) 输入一串数据,进行中序遍历,输入元素x,查找二叉排序树T,若存在含x的结点,则删除该结点,并作 中序遍历(执行操作2);否则输出信息“无x”。验证结果正确,说明其符合算法设计的要求:(1)正确 性、可读性、健壮性、效率与低储存量需求.要写一个优质的算法,就必须考虑其时间复杂度(它 表示随问题的规模n的增大,算法执行时间的增长率和f(n)的增长率相同)和空间复杂度。遍历 二叉树的算法中的基本操作是访问结点,则不论按那一次次序进行遍历,对含n个结点的二叉树, 其时间复杂度为O(n)。所需辅助空间为遍历过程中栈的最大容量,即树的深度log(n),最坏情况 下为n,则空间复杂度也为O(n)。 2.二叉排序树的中序遍历
3.二叉排序树中元素的查找
4.二叉排序树中元素的查找
三.算法思想
(一)程序设计思想
(二)程序模块
1.二叉链表结构(BST),C
2.顺序存储(BST),C
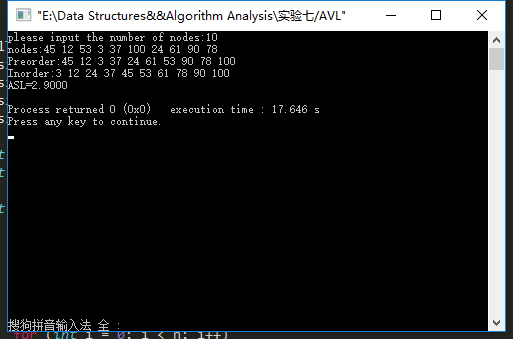
3.二叉链表(AVL),C
四.算法思想
(一)程序调试
(二)测试结果分析