DAY 1
B 组
T1 游戏
Description
Alice和Bob在玩一个游戏,游戏是在一个N*N的矩阵上进行的,每个格子上都有一个正整数。
当轮到Alice/Bob时,他/她可以选择最后一列或最后一行,并将其删除,
但必须保证选择的这一行或这一列所有数的和为偶数。如果他/她不能删除最后一行或最后一列,那么他/她就输了。
两人都用最优策略来玩游戏,Alice先手,问Alice是否可以必胜?
Input
第一行:T,表示数据组数
对于每组数据的第一行:N
接下来N行,每行N个数,描述这个矩阵
Output
如果Alice必胜输出W,否则输出L
Sample Input
2
2
2 4
6 8
3
5 4 2
1 5 9
7 3 8
Sample Output
L
W
Data Constraint
Hint
100%数据满足1<=N<=1000
保证每一行或每一列的和不会超过2*10^9
1<=T<=5
30%数据满足
1<=N<=5
50%数据满足
1<=N<=100
70%数据满足
1<=N<=500
正解
记忆化搜索,把必胜状态设为1,必输状态设为0,能到1的就是1,否则就是0
从一个小区域,一点一点往外扩从而进行搜索。最后记得特判一下能否去取这一行OR列
code
#include
#include
#include
using namespace std;
int dp[1050][1050],n,t;
int x[1050][1050],map[1050][1050];
int main(){
//freopen("game10.in","r",stdin);
//freopen("1.out","w",stdout);
scanf("%d",&t);
while(t--){
memset(dp,0,sizeof(dp));
memset(x,0,sizeof(x));
memset(map,0,sizeof(map));
scanf("%d",&n);
for(register int i=1;i<=n;i++)
for(register int j=1;j<=n;j++)
scanf("%d",&map[i][j]);
for(register int i=1;i<=n;i++)
for(register int j=1;j<=n;j++)
x[i][j]=map[i][j]+x[i-1][j]+x[i][j-1]-x[i-1][j-1];
dp[1][1]=!(map[1][1]%2==0);
for(register int i=1;i<=n;i++){
for(register int j=1;j<=n;j++){
if(i==1&&j==1) continue;
if((i>1&&(x[i][j]-x[i-1][j])%2==0&&dp[i-1][j]==0)||(
j>1&&(x[i][j]-x[i][j-1])%2==0&&dp[i][j-1]==0))
dp[i][j]=1;
else dp[i][j]=0;
}
}
if(dp[n][n]) printf("W\n");
else printf("L\n");
}return 0;
}
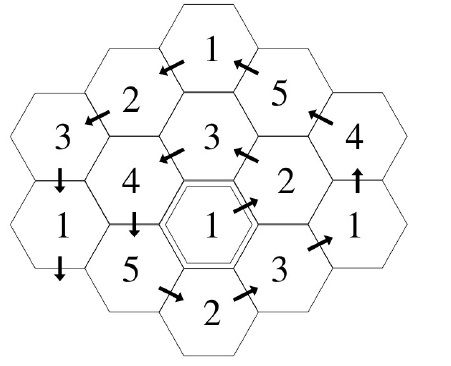
T2 六边形
Description
棋盘是由许多个六边形构成的,共有5种不同的六边形编号为1到5,棋盘的生成规
则如下:
1.从中心的一个六边形开始,逆时针向外生成一个个六边形。
2.对于刚生成的一个六边形,我们要确定它的种类,它的种类必须满足与已生成的相
邻的六边形不同。
3.如果有多个种类可以选,我们选择出现次数最少的种类。
4.情况3下还有多个种类可以选,我们选择数字编号最小的。
现在要你求第N个生成的六边形的编号?
前14个六边形生成图如下:
nput
第一行:T,表示数据组数
接下来T行,每行一个数:N,表示第N个六边形
Output
共t行,每行一个数,表示第N个数据的答案
Sample Input
4
1
4
10
100
Sample Output
1
4
5
5
Data Constraint
Hint
100%数据满足
1<=T<=20
1<=N<=10000
30%数据满足
1<=N<=100
正解
first.数数,然后可以发现每一层都比里面一层多6个。然后通过这件事情去看第几个空大致在哪里。然后再通过它位置是什么样子的,就可以大致知道它里圈位置上是什么,然后按题意模拟,只要记得有些特殊的地方,例如六边形的六个角所影响的空数目以及位置都不同,特判一下就可以了
second.由观察不难发现,每一个空都要链接六个六边形,所以把每一个空的六边形都看作单独的一层,把每一圈都扩展,即可得到答案
third,可以把六边形摊开成为四边形,摊成矩形即可。
code
像我这么懒的人,代码还没有写,所以我才敢毫无顾忌的放上三种方法啊。
略略略,你来打我啊,嘻嘻嘻
T3 数列
Description
给你一个长度为N的正整数序列,如果一个连续的子序列,子序列的和能够被K整
除,那么就视此子序列合法,求原序列包括多少个合法的连续子序列?
对于一个长度为8的序列,K=4的情况:2, 1, 2, 1, 1, 2, 1, 2 。它的答案为6,子序列
是位置1->位置8,2->4,2->7,3->5,4->6,5->7。
Input
第一行:T,表示数据组数
对于每组数据:
第一行:2个数,K,N
第二行:N个数,表示这个序列
Output
共T行,每行一个数表示答案
Sample Input
2
7 3
1 2 3
4 8
2 1 2 1 1 2 1 2
Sample Output
0
6
Data Constraint
Hint
100%数据满足
1<=T<=20
1<=N<=50000
1<=K<=1000000
序列的每个数<=1000000000
30%数据满足
1<=T<=10
1<=N,K<=1000
正解
之前明明做过,我还忘了
每次都把和给mod一下,开个桶,统计一下余数。余数相组合也可以被整除的,就是答案的贡献之一。
code
#include
#include
#include
using namespace std;
#define int long long
int n,val[1001000],t,k,sum,x;
signed main(){
//freopen("seq2.in","r",stdin);
//freopen("b.out","w",stdout);
scanf("%lld",&t);
while(t--){
memset(val,0,sizeof(val));
scanf("%lld%lld",&k,&n);sum=0;int ans=0;
for(register int i=1;i<=n;i++){
scanf("%lld",&x);
sum+=x;val[sum%k]++;
sum%=k;
}
for(register int i=0;i
A 组
T1 水叮当的舞步
Description
为了讨好她的偶像虹猫,水叮当决定在地毯上跳一支轻盈的舞来卖萌~~~
地毯上的格子有N行N列,每个格子用一个0~5之间的数字代表它的颜色。
水叮当可以随意选择一个0~5之间的颜色,然后轻轻地跳动一步,地毯左上角的格子所在的联通块里的所有格子就会变成她选择的那种颜色。这里连通定义为:两个格子有公共边,并且颜色相同。
由于水叮当是施展轻功来跳舞的,为了不消耗过多的真气,她想知道最少要多少步才能把所有格子的颜色变成一样的。
Input
每个测试点包含多组数据。
接下来一个N*N的矩阵,矩阵中的每个数都在0~5之间,描述了每个格子的颜色。
N=0代表输入的结束。
Output
Sample Input
2
0 0
0 0
3
0 1 2
1 1 2
2 2 1
0
Sample Output
0
3
Data Constraint
对于50%的数据,N<=6
对于70%的数据,N<=7
对于100%的数据,N<=8,每个测试点不多于20组数据
正解
其实就是一个IDA* 的搜索,原题详见洛谷的flood-it
估价函数就是看看每次走完之后还有多少块颜色不同,把颜色数目记录一下。
每次最好可以减少一个不同的颜色数,所以已走步数加上剩余颜色数若大于已得到的最小步数,则可以剪枝
code
既然有原题,为何还要在这里找QAQ(才不是自己没调出来最后看了别人的代码的缘故呢)(哼唧)
T2 Vani和Cl2捉迷藏
Description
vani和cl2在一片树林里捉迷藏……
这片树林里有N座房子,M条有向道路,组成了一张有向无环图。
树林里的树非常茂密,足以遮挡视线,但是沿着道路望去,却是视野开阔。如果从房子A沿着路走下去能够到达B,那么在A和B里的人是能够相互望见的。
现在cl2要在这N座房子里选择K座作为藏身点,同时vani也专挑cl2作为藏身点的房子进去寻找,
为了避免被vani看见,cl2要求这K个藏身点的任意两个之间都没有路径相连。
为了让vani更难找到自己,cl2想知道最多能选出多少个藏身点?
Input
第一行两个整数N,M。
接下来M行每行两个整数x、y,表示一条从x到y的有向道路。
Output
一个整数K,表示最多能选取的藏身点个数。
Sample Input
4 4
1 2
3 2
3 4
4 2
Sample Output
2
Data Constraint
对于20% 的数据,N≤10,M<=20。
对于60% 的数据, N≤100,M<=1000。
对于100% 的数据,N≤200,M<=30000,1<=x,y<=N。
正解
n的范围不大,而题干中又有“两两之间关系”这种词,所以我们容易想到传递闭包
在把他们之间的关系转化之后,就是求二分图最小路径覆盖了。
最小路径覆盖=n-最大匹配数
感性理解一下吧,尽管我不太能说清为什么这么干,但是我的直觉告诉我这是对的(づ ̄ 3 ̄)づ
这有个大佬的博客,大家实在不理解就去这里吧。看我ヾ(•ω•`)o
code
1 #include2 #include 3 #include 4 #include 5 using namespace std; 6 int map[410][410],n,m,match[410],vis[410],x,y; 7 inline int read(){ 8 char c=getchar();int f=1,x=0; 9 while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} 10 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} 11 return f*x; 12 } 13 inline bool dfs(int x){ 14 for(register int i=1;i<=n;i++){ 15 if(!vis[i]&&map[x][i]){ 16 vis[i]=1; 17 if(!match[i]||dfs(match[i])){ 18 match[i]=x;return true; 19 } 20 } 21 }return false; 22 } 23 inline void floyed(){ 24 for(register int i=1;i<=n;i++) 25 for(register int j=1;j<=n;j++) 26 for(register int k=1;k<=n;k++) 27 map[i][j]|=map[i][k]&map[k][j]; 28 } 29 int main(){ 30 n=read();m=read(); 31 for(register int i=1;i<=m;i++) 32 map[read()][read()]=1; 33 floyed();int ans=0; 34 for(register int i=1;i<=n;i++){ 35 memset(vis,false,sizeof(vis)); 36 if(dfs(i)) ans++; 37 }printf("%d\n",n-ans); 38 }
T3 粉刷匠
Description
现在,神庙里有N根排列成一直线的石柱,从1到N标号,长老要求用油漆将这些石柱重新粉刷一遍。
喜欢思考的赫克托不仅没有立刻开始粉刷,反而开始琢磨一些奇怪的问题,比如,一共有多少种粉刷的方案?
为了让赫克托尽快开始粉刷,请你尽快告诉他答案。
Input
对于每一组测试数据数据:
第1行:一个正整数K
第2行:K个正整数,表示第i桶油漆可以粉刷的石柱个数,Ci。
Output
Sample Input
3
3
1 2 3
5
2 2 2 2 2
10
1 1 2 2 3 3 4 4 5 5
Sample Output
10
39480
85937576
Data Constraint
50% N≤15, T≤5
80% K≤15,Ci≤5,T≤500
100% K≤15,Ci≤6,T≤2000
在ZJOJ上,我调出来的正解只有组合数+DP,但是在其他地方,由于放开了空间限制,可以用7维记忆化搜索来切题的
1 inline int dfs(int a,int b,int c,int d,int e,int f,int last){ 2 if(~dp[a][b][c][d][e][f][last]) 3 return dp[a][b][c][d][e][f][last]; 4 if(a==0 && b==0 && c==0 && d==0 && e==0) 5 return dp[a][b][c][d][e][f][last]=1; 6 int ans=0; 7 if(a&&a-(last==2)>0) 8 ans+=(a-(last==2))*dfs(a-1,b,c,d,e,f,1); 9 if(b&&b-(last==3)>0) 10 ans+=(b-(last==3))*dfs(a+1,b-1,c,d,e,f,2); 11 if(c&&c-(last==4)>0) 12 ans+=(c-(last==4))*dfs(a,b+1,c-1,d,e,f,3); 13 if(d&&d-(last==5)>0) 14 ans+=(d-(last==5))*dfs(a,b,c+1,d-1,e,f,4); 15 if(e&&e-(last==6)>0) 16 ans+=e*dfs(a,b,c,d+1,e-1,f,5); 17 if(f) 18 ans+=e*dfs(a,b,c,d,e+1,f-1,6); 19 return dp[a][b][c][d][e][f][last]=ans%mod; 20 }
SECOND.组合数+DP
(至今不会用LETAX的菜鸡落下了伤心的泪水இ௰இ)
大家看这位大佬吧,我真的不想再打LETAX了,我对数学公式有着深深的心理阴影,至今为止,我还有一篇博客由于数学公式的缘故还在咕咕咕,嘤嘤嘤,你看我这么可爱,我卖个蠢,就放过我吧*★,°*:.☆( ̄▽ ̄)/$:*.°★* 。(才不是因为自己还有好几天总结没写而犯懒)
看这里看这里ヾ(•ω•`)o
CODE(其实楼上链接里有代码了QAQ)
1 #include2 #include 3 #include 4 using namespace std; 5 #define int long long 6 int t,n,ci[20],f[200][100],k; 7 int sum[20],c[105][105]; 8 const int mod=1000000007; 9 signed main(){ 10 c[0][0]=1; 11 for(register int i=1;i<=100;i++){ 12 c[i][0]=c[i][i]=1; 13 for(register int j=1;j<=i-1;j++) 14 c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; 15 }//组合数预处理 16 scanf("%lld",&t); 17 while(t--){ 18 scanf("%lld",&n); 19 for(register int i=1;i<=n;i++) 20 scanf("%lld",&ci[i]),sum[i]=sum[i-1]+ci[i]; 21 memset(f,0,sizeof(f));f[1][sum[1]-1]=1; 22 for(register int i=2;i<=n;i++) 23 for(register int j=0;j<=sum[i-1];j++) 24 if(f[i-1][j]) 25 for(register int k=1;k<=ci[i];k++) 26 for(register int t=0;t<=min(k,j);t++) 27 f[i][j+ci[i]-t-k]+=f[i-1][j]*c[j][t]*c[ci[i]-1][k-1] 28 *c[sum[i-1]+1-j][k-t], 29 f[i][j+ci[i]-t-k]%=mod; 30 printf("%lld\n",f[n][0]); 31 } 32 }