DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法将簇看做高密度区域以从低密度区域中区分开。由于这个算法的一般性,DBSCAN建立的簇可以是任何形状的。相对的,K-means则假设簇是凸的。核样本的概念是DBSCAN的重要成分,核样本是指高密度区域的样本。一个簇是由互相靠近的核样本的集合以及靠近核样本的非核样本组成的集合组成的。这个算法有两个参数,
min_samples和 eps ,这两个参数表示数据的稠密性。当min_samples增加 或者 eps 减小的时候,意味着一个簇分类有更大的密度要求。
若样本在数据集中存在eps距离内有至少min_samples,则该样本可以成为核样本。也用来定义边缘样本。核样本是向量空间的高密度区域。通过找到一个核样本,找到其附近的核样本,再找到附近核样本的附近的核样本递归地建立由核样本组成的簇。一个簇也包含邻居是核样本的非核样本。
根据定义,任何核样本是簇的一部分。任何距离核样本至少eps距离非核样本是异常值。
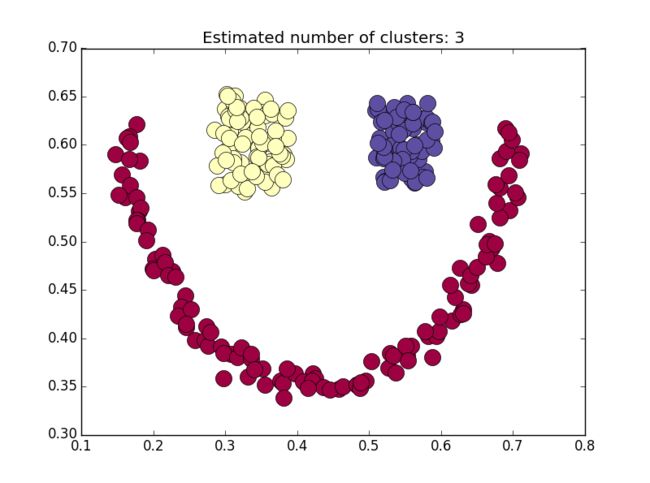
从下图中可以看到,不同的颜色表示不同的簇。大圈圈表示算法定义的核样本,小圈圈表示仍是簇的组成部分的非核样本。黑色点表示异常值。
实现
这个算法是有随机性的,虽然标签会变化,但是核样本始终属于同一个簇。非确定性主要来自非核样本的归属。一个非核样本可能距离两个簇的非核样本都小于eps 。根据三角不等式,这两个核样本之间的距离大于eps,否则他们会属于同一个簇。非核样本将会属于先产生的簇,而簇产生的先后顺序是随机的。不考虑数据集的顺序,算法是确定性的,相同数据上的 结果也会相对稳定。
当先实现是使用球树和线段树来计算点的邻居,这避免了计算时全距离矩阵。可以使用一般的距离度量方法。
内存消耗
当前实现不是一个节约内存的算法,因为它建立了kd-tree和ball-tree不能使用的成对的相似矩阵。可以绕过这个的方法如下:
- 可以通过metric='precomputed'计算稀疏的半径临近图,这会节省内存使用。
- 数据可以压缩,或者使用BIRCH去掉数据中的重复值。然后大量的数据集将由小部分数据代表,可以使用sample_weight来拟合算法
使用说明
class sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean', algorithm='auto', leaf_size=30, p=None, n_jobs=1)
| 参数 | 说明 |
|---|---|
| eps | float,可选 |
| min_samples | int,可选 |
| metric | string,用于计算特征向量之间的距离 |
| algorithm | {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’},可选 |
| leaf_size | 传递给球树,影响速度、内存,根据情况自己选择 |
| p | 明氏距离的幂次,用于计算距离 |
| n_jobs | CPU并行数 |
| 方法 | 说明 |
|---|---|
| fit(X[, y, sample_weight]) | 从特征矩阵进行聚类 |
| fit_predict(X[, y, sample_weight]) | 实行聚类并返回标签(n_samples, n_features) |
| get_params([deep]) | 取得参数 |
| set_params(**params) | 设置参数 |
| 属性 | 类型 | 大小 | 说明 |
|---|---|---|---|
| core_sample_indices_ | array | [n_core_samples] | 核样本的目录 |
| components_ | array | [n_core_samples, n_features] | 训练样本的核样本 |
| labels_ | array | [n_samples] | 聚类标签。噪声样本标签为-1 |
例子
程序地址:http://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html#sphx-glr-auto-examples-cluster-plot-dbscan-py
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler
##############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
random_state=0)
X = StandardScaler().fit_transform(X)
##############################################################################
# Compute DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
print('Estimated number of clusters: %d' % n_clusters_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, labels))
##############################################################################
# Plot result
import matplotlib.pyplot as plt
# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
for k, col in zip(unique_labels, colors):
if k == -1:
# Black used for noise.
col = 'k'
class_member_mask = (labels == k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
应用
关键在于调节前面提到的两个参数,需要不断修正。如果需要测试数据,可以留言。
import scipy.io as sio
import numpy as np
from sklearn.cluster import DBSCAN
#from sklearn import metrics
import matplotlib.pyplot as plt
data_smile = sio.loadmat('data\smile.mat')
X = data_smile['smile'][:, :2]
labels_true = data_smile['smile'][:, 2]
db = DBSCAN(eps=0.05, min_samples=3).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
for k, col in zip(unique_labels, colors):
if k == -1:
# Black used for noise.
col = 'k'
class_member_mask = (labels == k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
参考
- “A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise” Ester, M., H. P. Kriegel, J. Sander, and X. Xu, In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, AAAI Press, pp. 226–231. 1996
- 概要:http://scikit-learn.org/stable/modules/clustering.html#dbscan
- 参数说明:http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html#sklearn.cluster.DBSCAN