一、三种颜色空间
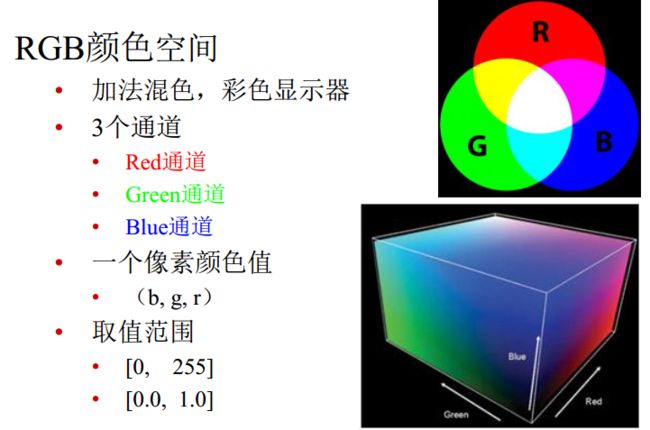
“加法混色”的含义:越混合越亮。
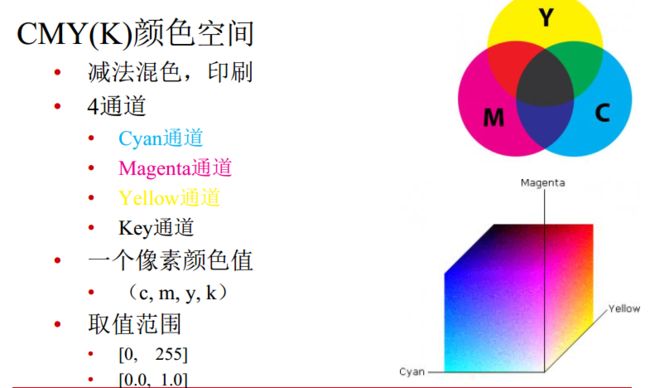
“减法混色”的含义:越混合越暗。
圆锥形代表了HSV颜色空间的三要素:比如饱和度,越接近圆心越不饱和/不纯,即越来越白。
二、图片存储原理
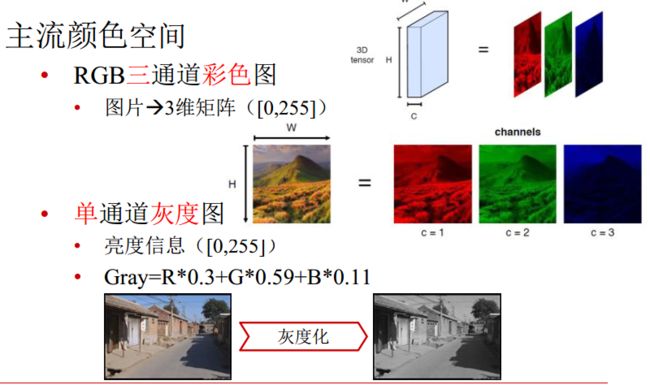
三通道彩色图片:红+绿+蓝
(三通道)彩色图变成(单通道)灰度图:R,G,B的系数之和为1即可。
RGB图片的数据格式:
R,G,B矩阵的同一位置的数值可能是各不相同的。
图片存储格式:
BMP就是用RGB三个矩阵存图。位映射可能是256位:0-255,也可能是16位:0-15。
JPG用的是离散余弦变换来压缩,可以压缩到很小。
三、图像增强
目标:突出有意义信息,同时抑制无意义信息。
方法:
1、直方图均衡
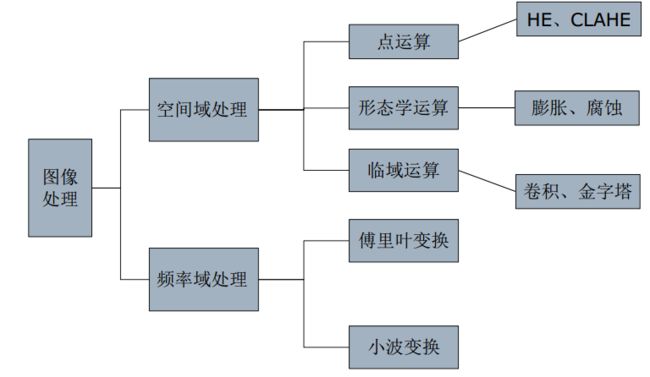
空间域处理——>点运算——>HE(直方图均衡):
点运算:每个点的亮度进行变化,与周围的点没有关系。
直方图(Histogram):统计某一色阶一共有几个点。 数据空间(bin)
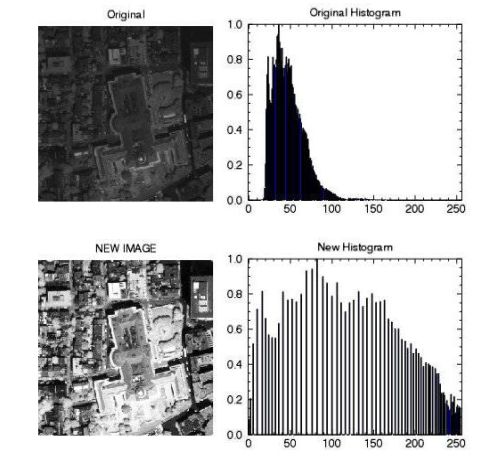
直方图均衡化:对图像进行非线性拉伸。(比如比较黑的地方更黑,比较白的地方更白。)
例如:
直方图均衡的缺陷:不适用于某些地方较暗,但是某些地方特别亮的图片。
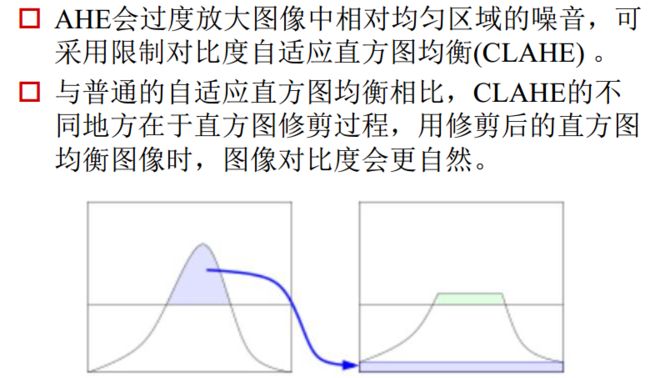
自适应直方图均衡:解决了直方图均衡的缺陷。
自适应直方图均衡(CLACHE)
原理:
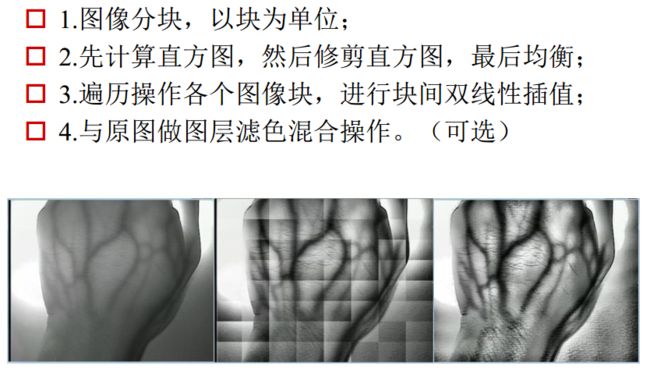
举例:
进行第二步之后每一个块会变得不连续,所以要进行第三步操作。
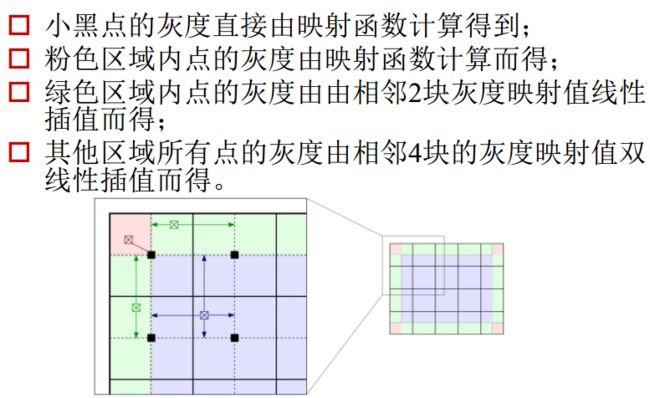
第三步双线性差值算法的介绍:
评价:增强图片对比度的目前所知的最好的办法。
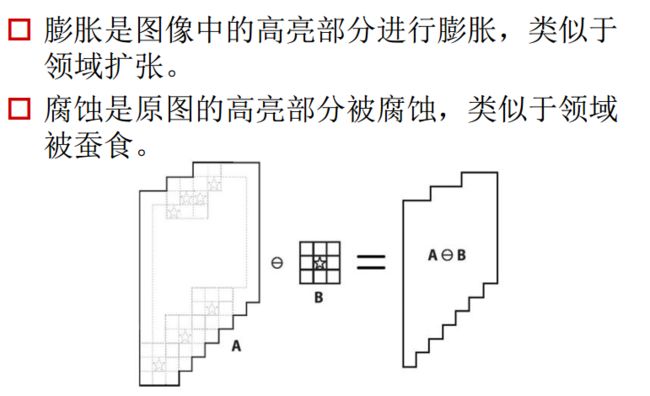
2、形态学运算(腐蚀和膨胀)
膨胀和腐蚀的基本介绍如下:
A+B——>AB是腐蚀,反过来AB——>A+B是膨胀(B的五角星的位置对着AB边界过一圈)。
开运算可以去掉目标外的孤立点,闭运算可以去掉目标内的孔。
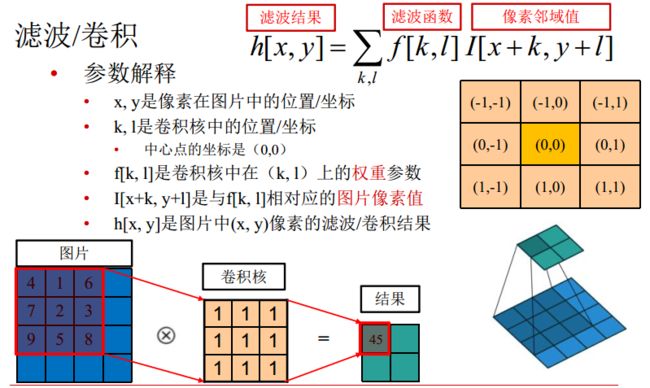
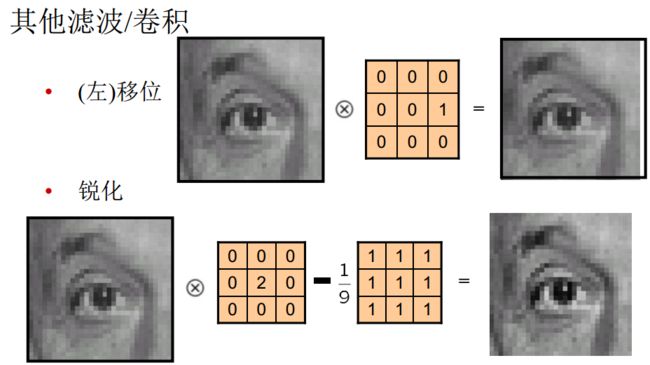
3、空间域处理及变换:滤波/卷积
注意:滤波实际上就是卷积....
概述:
重点是对公式的理解:
右侧橙色3*3矩阵内显示的是k和l的取值。f代表卷积核,I表示图片上对应点的像素值。
边界填充:为了使得卷积后的图片与卷积前的图片大小相同,需要进行边界填充。
最常见的方式是补零。
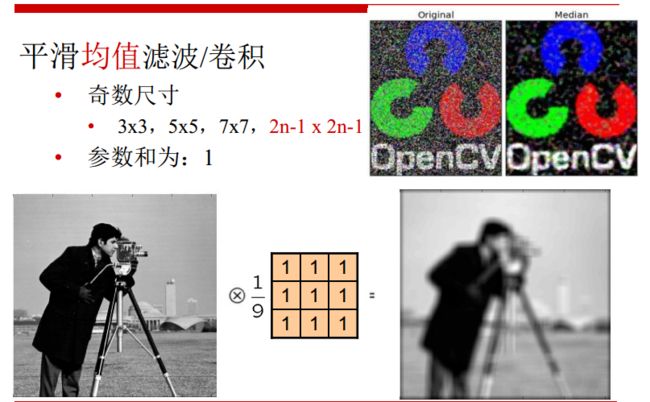
均值滤波:
平滑均值滤波/卷积:
效果:
评价:
均值滤波本身存在缺陷,既没有很好地去除噪声点,也破坏的图像的细节,反而使图片变得模糊。
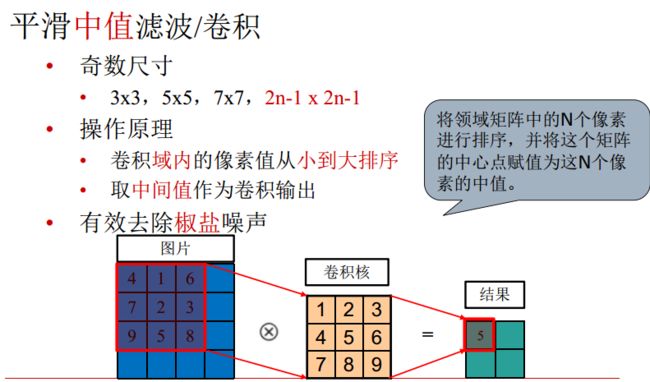
中值滤波
效果如下:
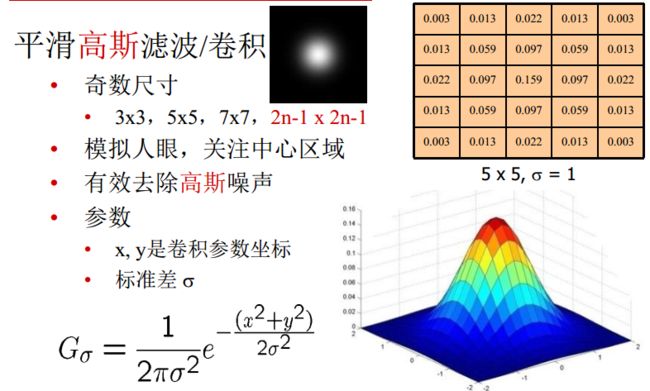
高斯滤波
特点:模拟人眼特性,离关注中心越远,感受图像越模糊。
举例:标准差sigma是卷积核的重要参数。
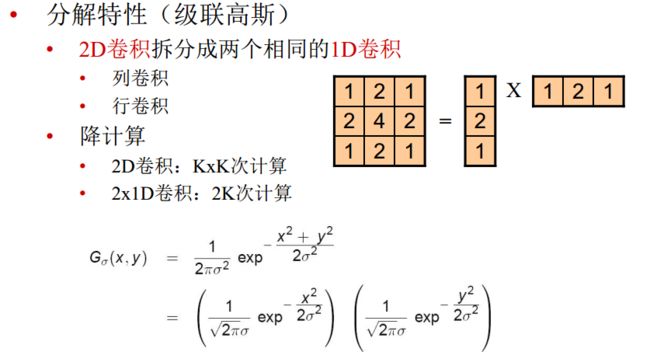
二维卷积的重要特性:
通过拆分可以降低运算次数。
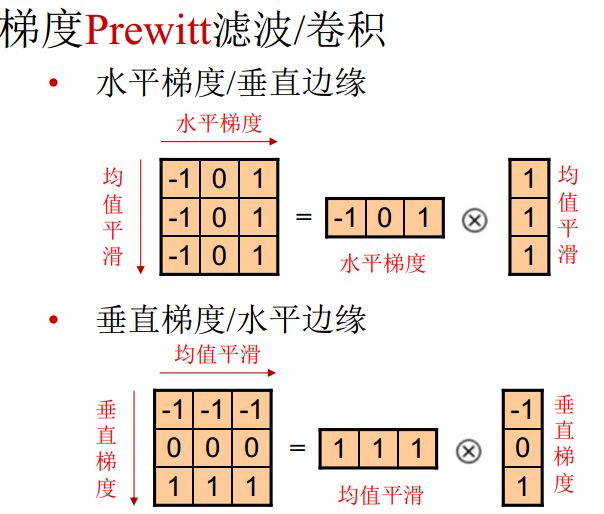
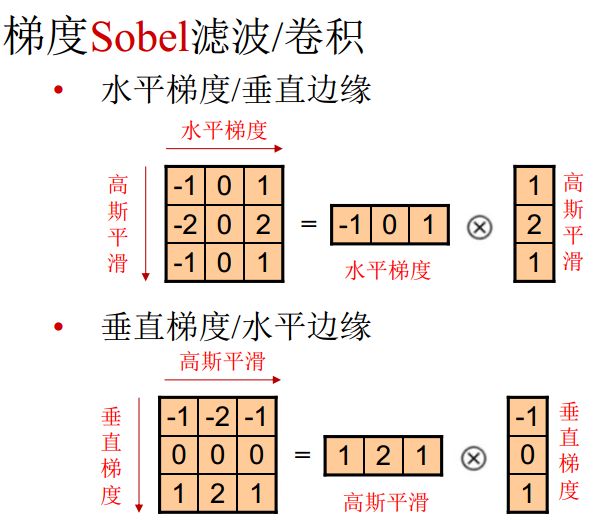
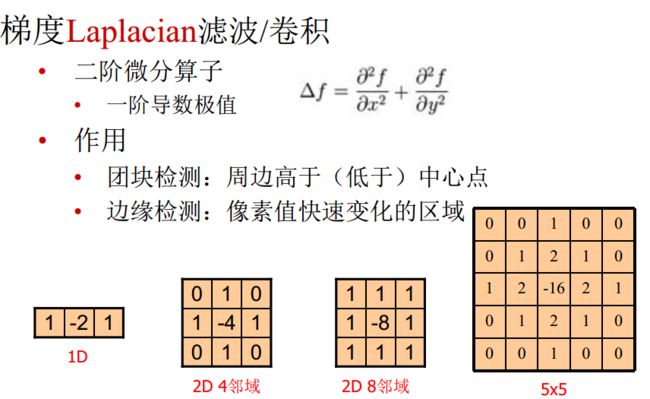
梯度滤波
拉普拉在算子的缺点:对噪声的边缘也很敏感。
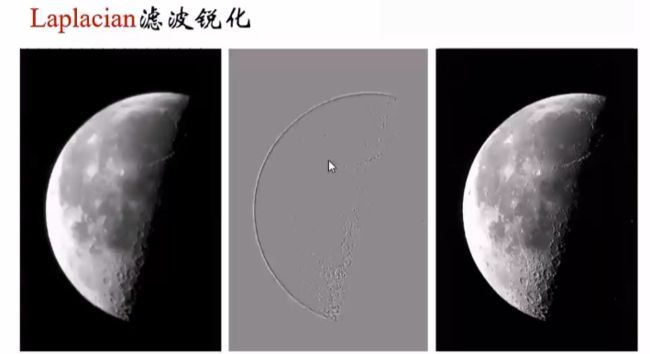
举例:
第二幅图为进行了拉普拉斯算子滤波后的图,第一张原图减第二张图,得到了第三张图:月面上的环形山变得非常清晰。
4、频域处理
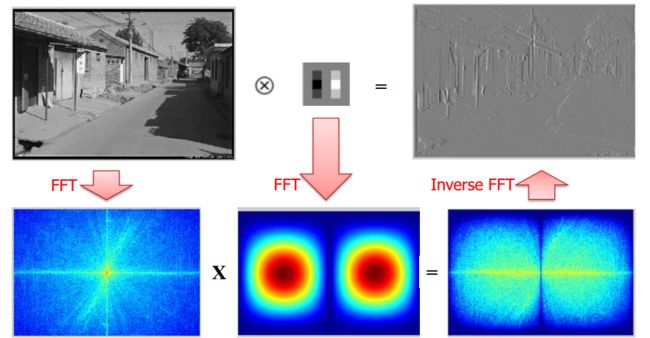
空域卷积=频域乘积
一个信号可以由足够多个不同频率和幅值的正弦波组成。
如上图所示:原图FFT和卷积核(算子FFT),然后两者的FFT相乘,再IFFT。
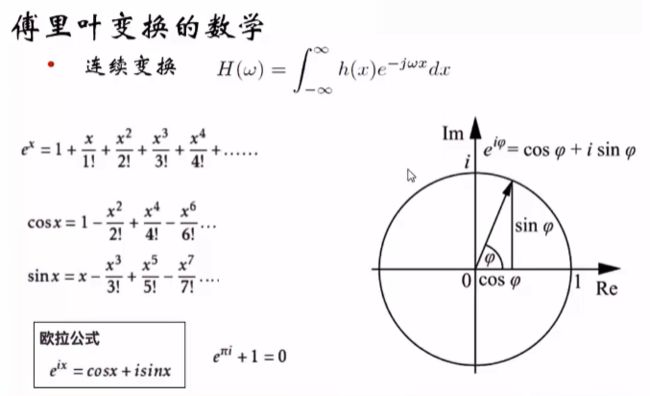
傅里叶变换的数学原理:
连续变换公式里的-jwt里面的-可以看成是除法的含义,原信号除以正弦波的格式,就变成了振幅。
逆变换公式反映了:一个信号可以由足够多个不同频率和幅值的正弦波组成。
具体来看:F(w)代表正弦波的幅值,e^(iwt)与幅值结合就成为了正弦波。
以上是连续傅里叶变换,如下是离散傅里叶变换:
注意:是横纵颠倒的,MN互换
零点在图片的正中央。
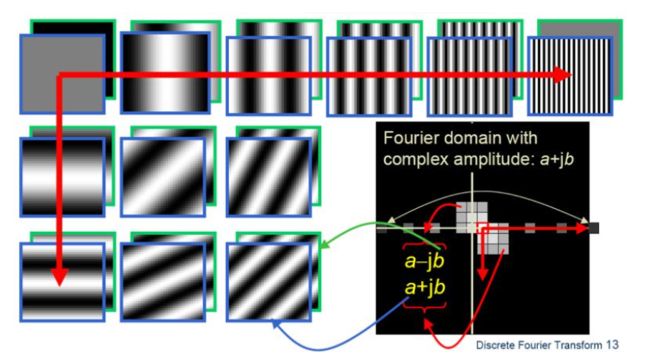
二维离散傅里叶变换的本质:找到二维图片的基图片。
Y轴方向(竖线)的基图片是横向的正弦曲线,X轴方向(竖线)的基图片是纵向的正弦曲线。
a-jb和a+jb这里既有实部又有虚部,对应于基图片中倾斜的那些图片。
傅里叶变换应用举例:
基于傅里叶变换的滤波
低通主要反映宏观信息,高通反映细节信息。黑色部分就是指遮住了这部分的频谱。
仔细看图,第一张FFT图中心有竖线,对应原图中横向排列的门框。
下面的例子中,第一幅图被叠加了纵向的正弦函数,在频谱图中反映为横向的一排亮点。把亮点覆盖掉,就可以滤掉噪声。
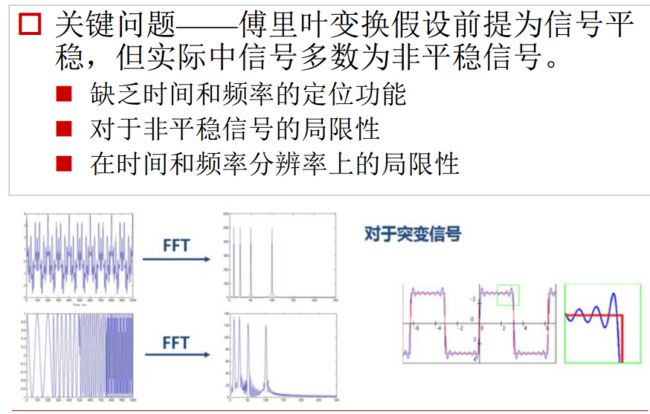
傅里叶变换的缺点:
比如左下两图,频谱其实长得很像,难以区分非稳定信号(疏密相间)与稳定信号。
此外,对于突变信号,往往会在边缘呈现锯齿形,因为现实生活中累加是有限的。
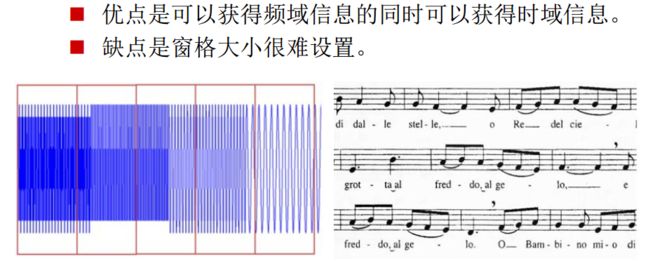
针对非平稳信号的问题,提出了加窗傅里叶变换的方法:
认为在一个窗内,信号是平稳的。然后对窗格内的信号分段进行傅里叶变换。
类似五线谱一个音持续的时间。
小波变换
其实小波变换更符合实际情况,因为很多时候是短暂的突变而不是稳定的正弦波。
常见的小波函数:
5、高斯金字塔和拉普拉斯金字塔
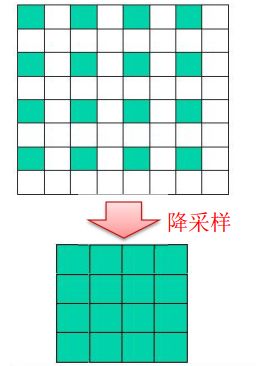
图片进行降采样(高分辨率——>低分辨率)的过程中,若直接降采样,图片会不连续。
因此需要采用高斯金字塔,先进行图像平滑,再进行降采样。
举例:
其中,没经过高斯金字塔的图看起来不连续。
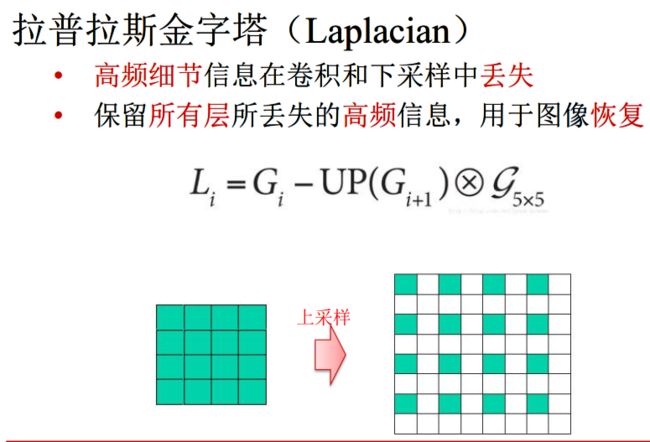
拉普拉斯金字塔和高斯金字塔是配套使用的。
拉普拉斯金字塔是如何得出的:
降采样之后的高斯金字塔的图无法恢复成原图,需要补充细节轮廓信息,这个信息就是拉普拉斯金字塔。
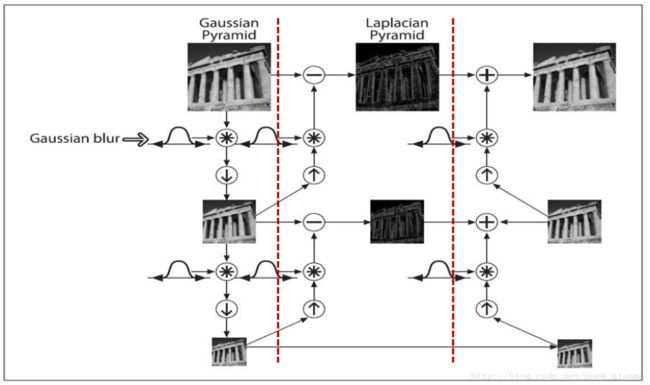
下图中,第一列为高斯金字塔,第二列为拉普拉斯金字塔,两者相加,即为原图。
这样做的意义:高斯金字塔一层一层代表了宏观的图片信息,拉普拉斯金字塔代表了图片的微观细节和轮廓信息。