最近遇到了复杂多分类问题,因为无论在自己平时生活还是导师或老板分配的任务里都很常见,所以打算写写,记录下点点滴滴。
复杂多分类问题
什么是复杂多分类问题?(复杂多分类是我自己命名的,如果命名错误请谅解)用一个例子来告诉大家:
比如有一天zenRRan盗窃了东西的时候,被店主人发现,于是两人发生了争执,zenRRan就动手打了人家并且拿了值钱的东西跑了。最后警察根据路边监控的人脸识别功能,识别到了我在xxx大学实验楼NLP实验室312lab,于是将之逮捕!
如果你是大法官,你会判他什么罪?(不要怕,zenRRan不会生气)在找罪名的时候,大脑里先过一遍所有的罪名,以防漏掉一个。这时大脑扫描到了盗窃罪,再一看整个案件,对,zenRRan犯了盗窃罪;之后又扫到了贩卖枪支罪,然后和我的案例一对比,不符合;最后根据上述的流程,发现我又犯了故意伤人罪。最终判别:zenRRan犯了盗窃罪,故意伤人罪,数罪并罚
上述问题就是复杂多分类问题。首先罪行数量是一定的,分类结果就是从这些罪行数量中选择。你肯定会联想到咱们平时见得简单分类问题。但是复杂多分类问题和简单分类问题的区别是,前者可以从已知分类集合中选取若干种,而后者只能选取一种。
现在你应该清楚什么是复杂多分类问题了,那么又是怎么训练的呢?代码中又是怎么写呢?毕竟理论和实践毕竟是两件事,下面来讲述下复杂多分类问题我的思路历程和简单网络模型代码搭建。
网络训练思路历程
我从我当时第一次写该模型的时候的思路流程来一一讲解。我的思路流程应该就是大家的思路流程了。
比如训练集为:
case1:杀人罪
case2:故意伤人罪,破坏公物罪
case3:盗窃罪,故意伤人罪
首先,因为我认为复杂多分类问题和简单分类问题极为类似,所以就按照简单分类问题那样,每个case的label是一个label,于是最终分类为结果为:三类,分类集合为:
【杀人罪】,【故意伤人罪,破坏公物罪】,【盗窃罪,故意伤人罪】
于是被导师看到了,用鄙视的小眼神看着我,并说:以后别说你导师是我,我没有这样的学生
。于是又耐心的点播我:神经网络和人的思路得是一样的,因为神经网络就是在模仿人类大脑的思考方式,所以,你再想想自己是怎么思考的?然后怎么用网络表示出来?
于是恍然大悟,茅塞顿开,柳暗花明又一村。
想了想上述描述的例子我的大脑是怎么个流程,于是有了新的思路。
因为对每一个案例判刑,需要扫描的集合是所有的罪行,然后进行判定是or否。于是得到分类集合为:
【杀人罪】,【故意伤人罪】,【破坏公物罪】,【盗窃罪】
即在所有罪行上进行二分类。这里用1表示是,0表示否。
所以case1的训练的金标为:
1 0 0 0
case2训练金标为:
0 1 1 0
case3训练金标为:
0 1 0 1
大致思路就是上面的,我想你应该是懂了。然后代码实践。
网络模型代码搭建
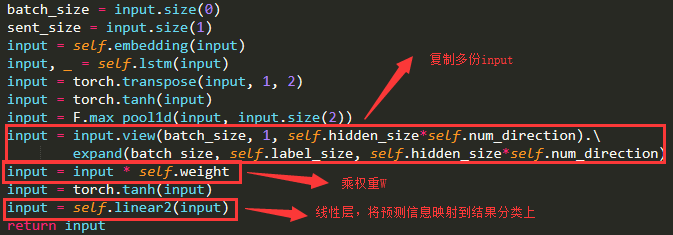
网络的大部分内容和简单分类任务网络搭建还是很相似的,先是case通过embedding层,然后LSTM层,之后获得结果,然后进行max_pooling,代码为:
最后的input中保存了这个case的被提取的信息。
我们之后要做的就是在这个input上进行复杂多分类预测。我们继续想大脑的思考过程,是对一个案例在所有类上做二分类,需要有一个参数W。
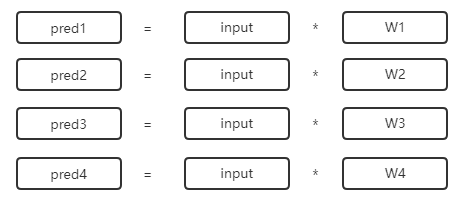
如对第一个罪行进行预测:
pred1 = input * W1
对第二个罪行进行预测:
pred2 = input * W2
对第三个罪行进行预测:
pred3 = input * W3
对第四个罪行进行预测:
pred4 = input * W4
注:input维度为(1, hidden_size),Wi 维度为(1,hidden_size),得到预测信息为predi,维度为(1,hidden_size)
具体表示为:
我们能够看出,每一个式子中的input是一样的,只是Wi不一样而已,所以,为了加速计算,这里 Wi 可以用大矩阵来表示,input本身复制多份:
每一个case的预测信息保存在pred矩阵里,最后对pred进行线性分类即可。其中pred维度为(label_size,hidden_size),分类结果映射到(label_size,2)上。
代码为:
Summary
我们用神经网络搭建的时候,一定要想着自己的大脑思考过程,不要一个方法用到所有任务上。每个任务有每个任务的特点,对症下药才有效!
作者:zenRRan
链接:https://www.jianshu.com/p/f09cff556bfa
來源:
著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。