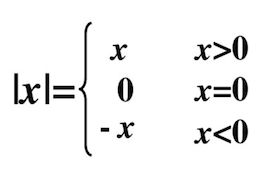机器学习的数学基础--微积分（1）--线坐标系，绝对值，不等式

线坐标系（Linear Coordinate System)

实数，是有理数和无理数的总称。前者为1，2，1/3等，后者为根号3，Pi等等。
线坐标系，就是一条带有方向的直线，任何一个实数，在线坐标上都有且只有一个点与之对应。
实数可以把线坐标系“填满”。

设置线坐标系的方式：

（1）选择一个点作为原点，该点的对应实数为0
（2）选择正实数的方向，也就是箭头的方向
（3）选择代表实数1的固定的单位距离。
线坐标系上的点所代表的数值被称作该点的“坐标”(coordinate)

线坐标系

绝对值

数x的绝对值|x|被定义为：

绝对值的定义

绝对值的性质

1，|-x| = |x|
2, |x - y| = |y - x|
3, 如果|x| = c 则 x = +c 或 x = -c
4, |x|² = x²
5, |x*y| = |x| * |y|
6, |x|/|y| = |x|/|y| 如果y不等于0
7, 如果|x| = |y| 则 x = +y 或x = -y
8, 令c>=0, 则当且仅当-c <= x <= c时，|x|<=c
9, 令c>=0, 则当且仅当-c < x < c时，|x| 10, -|x| <= x <= |x|
11, |x + y| <= |x| + |y|
12, |x₁ - x₂| = P₁P₂ = 线坐标系上点P₁（坐标x₁)到点P₂(坐标x₂)之间的距离
13, |x₁| = 线坐标系上点P₁(坐标x₁)到原点的距离

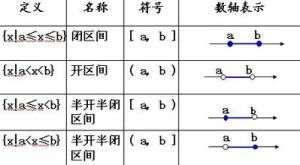
开区间，闭区间，无限区间

开区间

直线上介于固定的两点a和b之间的所有点的集合（不包含给定的两点），用(a,b)来表示，叫做开区间。
开区间的实质仍然是数集，该数集用符号（a，b）表示，含义一般是在实数a和实数b之间的所有实数，但不包含a和b。

闭区间

直线上介于固定的两点a和b之间的所有点的集合（包含给定的两点）。该集合用符号[a,b]表示。

开区间与闭区间

无限区间

我们可以用符号

来表示区间在某方向上无界。具体定义如下：

不等式

任何不等式，例如2x - 3 > 0 或者 5 < 3x + 10 <= 16, 决定了一个区间。解不等式，就是找到满足该不等式的区间。

例1，

解不等式2x - 3 > 0,
2x - 3 > 0
2x > 3
x > 3/2
解得x的区间：(3/2, 正无穷)

例2，

解不等式|x + 2| < 3,
由绝对值的性质，得出-3 < x + 2 < 3，则
-5

例3，

解不等式x² < 3x + 10
x² - 3x - 10 < 0
(x - 5)(x + 2) < 0
-2 < x < 5
x的区间：(-2, 5)

例4，

解不等式（2x + 1) / (x + 3) > 3
解决此不等式需要进行分条件讨论。
(1)当x + 3 > 0时，即x > -3时，不等式两边同时乘以x + 3，得：
2x + 1 > 3x + 9
则x < -8，与初始条件 x > -3 矛盾，则此条件不成立。
(2)当x + 3 < 0时，即x < -3时，不等式两边同时乘以x + 3并改变不等号，则得：
2x + 1 < 3x + 9,则x > -8,则：
-8 < x < -3, x 在区间(-3, -8)之间。

例5，

解不等式|2x - 5| >= 3
我们可以先解|2x - 5| < 3,则得：-3 < 2x - 5 < 3,则得：
1 < x < 4，（1，4）从而|2x - 5| >= 3的区间为：
x <= 1 或者 x >= 4

习题：

1， 2x - 1 / x < 3
2, |3x - 7 | > 2
3, x³ + 3x² > 10x