梯度下降法及一元线性回归的python实现

梯度下降法及一元线性回归的python实现

一、梯度下降法形象解释

　　设想我们处在一座山的半山腰的位置，现在我们需要找到一条最快的下山路径，请问应该怎么走？根据生活经验，我们会用一种十分贪心的策略，即在现在所处的位置上找到一个能够保证我们下山最快的方向，然后向着该方向行走；每到一个新位置，重复地应用上述贪心策略，我们就可以顺利到达山底了。其实梯度下降法的运行过程和上述下山的例子没有什么区别，不同的是我们人类可以凭借我们的感官直觉，根据所处的位置来选择最佳的行走方向，而梯度下降法所依据的是严格的数学法则来进行每一步的更新。本文不再对该算法进行严格的数理讨论，只介绍梯度下降法进行数据拟合的流程和利用梯度下降法解决一元线性回归的python实现。

二、梯度下降法算法应用流程

　　假设有一组数据X=[x₁,x₂,x₃,...]，Y=[y₁,y₂,y₃,...]，现求由X到Y的函数关系：

　　1、为所需要拟合的数据，构造合适的假设函数：y=f(x;θ)，以θ=[θ₁,θ₂,θ₃,...]为参数；

　　2、选择合适的损失函数：cost(θ)，用损失函数来衡量假设函数对数据的拟合程度；

　　3、设定梯度下降法的学习率 α，参数的优化初始值及迭代终止条件；

　　4、迭代更新θ，直到满足迭代终止条件，更新公式为：

　　　　θ₁=θ₁-α*dcost(θ)/dθ₁，

　　　　θ₂=θ₂-α*dcost(θ)/dθ₂，...

三、一元线性回归的python实现

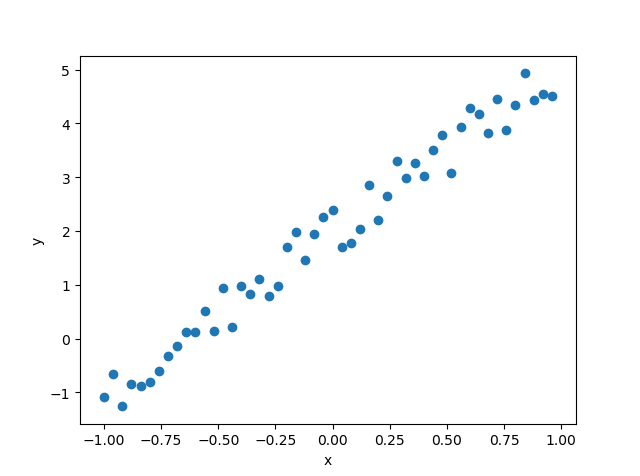
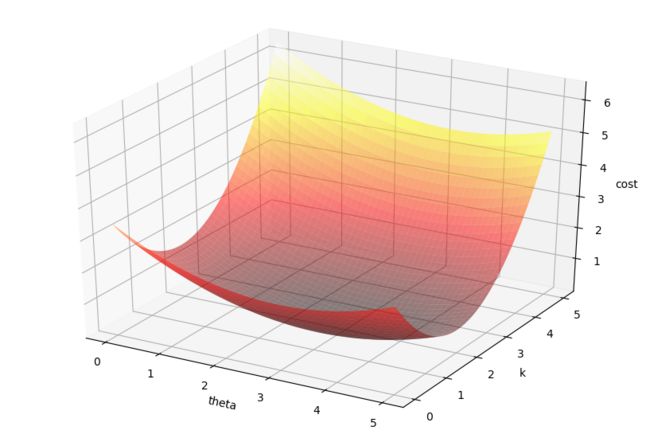
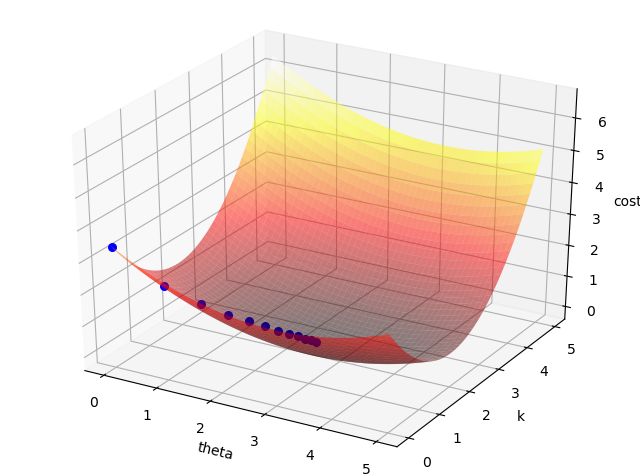
　　下面以一个一元线性回归的例子来更进一步理解梯度下降法的过程。笔者通过在函数y=3*x+2的基础之上添加一些服从均匀分布的随机数来构造如下的待拟合数据：X,Y，训练数据图像如下图1所示。假设函数为一元线性函数: y=f(x;θ,k)=θ*x+k，损失函数为:cost(θ,k)=1/2*∑(f(x_i;θ,k)-y_i),x_i属于X，y_i属于Y，损失函数的图像如下图2所示。应用梯度下降法进行参数更新的过程如图3中的蓝色圆点所示。　

 

（1）　

（2）

（3）

　　程序源代码如下：

 1 import numpy as np
 2 import matplotlib.pyplot as plt
 3 from mpl_toolkits.mplot3d import Axes3D
 4 
 5 np.random.seed(1)
 6 #生成样本数据
 7 x=np.arange(-1,1,step=0.04)#自变量
 8 noise=np.random.uniform(low=-0.5,high=0.5,size=50)#噪声
 9 y=x*3+2+noise#因变量
10 #显示待拟合数据
11 plt.figure(1)
12 plt.xlabel('x')
13 plt.ylabel('y')
14 plt.scatter(x,y)
15 
16 #假设函数为一元线性函数：y=theta*x+k，需要求解的参数为theta和k
17 #损失函数为
18 def cost(theta, k, x, y):
19     return 1/2*np.mean((theta*x+k-y)**2)
20 
21 def cost_mesh(theta_m, k_m, x, y):
22     z_m=np.zeros((theta_m.shape[0],theta_m.shape[1]))
23     for i in range(theta_m.shape[0]):
24         for j in range(theta_m.shape[1]):
25             z_m[i,j]=cost(theta_m[i,j], k_m[i,j],x,y)
26     return z_m
27 #可视化损失函数
28 theta_axis=np.linspace(start=0, stop=5,num=50)
29 k_axis=np.linspace(start=0, stop=5,num=50)
30 (theta_m, k_m)=np.meshgrid(theta_axis,k_axis)#网格化
31 z_m=cost_mesh(theta_m, k_m, x, y)
32 #绘制损失函数的3D图像
33 fig=plt.figure(2)
34 ax=Axes3D(fig)#为figure添加3D坐标轴
35 ax.set_xlabel('theta')
36 ax.set_ylabel('k')
37 ax.set_zlabel('cost')
38 ax.plot_surface(theta_m, k_m, z_m,rstride=1, cstride=1,cmap=plt.cm.hot, alpha=0.5)#绘制3D的表面, rstide为行跨度，cstride为列跨度
39 
40 
41 #梯度下降法
42 #参数设置
43 lr=0.01#学习率
44 epoches=600#迭代次数,即迭代终止条件
45 
46 #参数初始数值
47 theta=0
48 k=0
49 
50 #迭代更新参数
51 for i in range(epoches):
52     theta_gra=np.mean((theta*x+k-y)*x)#theta梯度
53     k_gra=np.mean(theta*x+k-y)#k梯度
54     #更新梯度
55     theta-=theta_gra*lr
56     k-=k_gra*lr
57     #绘制当前参数所在的位置
58     if i%50==0:
59         ax.scatter3D(theta, k, cost(theta, k, x,y), marker='o', s=30, c='b')
60 print('最终的结果为：theta=%f, k=%f'%(theta, k))
61 plt.show()