在日常工作计算中,我们如履薄冰,但是 JavaScript 总能给我们这样那样的 surprise~
- 0.1 + 0.2 = ?
- 1 - 0.9 = ?
如果小伙伴给出内心的结果:
- 0.1 + 0.2 = 0.3
- 1 - 0.9 = 0.1
那么小伙伴会被事实狠狠地扇脸:
console.log(0.1 + 0.2); // 0.30000000000000004
console.log(1 - 0.9); // 0.09999999999999998
为什么会出现这种情况呢?咱们一探究竟!
三 问题复现
返回目录
下面,我们会通过探讨 IEEE 754 标准,以及 JavaScript 加减的计算过程,来复现问题。
3.1 根源:IEEE 754 标准
返回目录
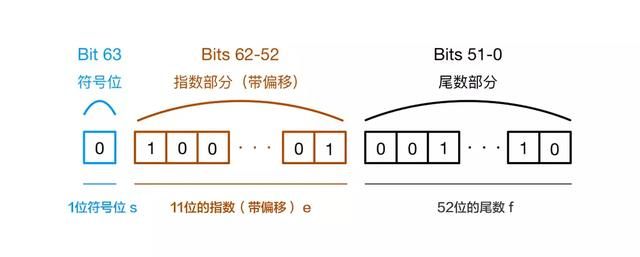
JavaScript 里面的数字采用 IEEE 754 标准的 64 位双精度浮点数。该规范定义了浮点数的格式,对于 64 位的浮点数在内存中表示,最高的 1 位是符号为,接着的 11 位是指数,剩下的 52 位为有效数字,具体:
- 第 0 位:符号位。用 s 表示,0 表示为正数,1 表示为负数;
- 第 1 - 11 位:存储指数部分。用 e 表示;
- 第 12 - 63 位:存储小数部分(即有效数字)。用 f 表示。
符号位决定一个数的正负,指数部分决定数值的大小,小数部分决定数值的精度。
IEEE 754 规定,有效数字第一位默认总是 1,不保存在 64 位浮点数之中。
也就是说,有效数字总是 1.XX......XX的形式,其中 XX......XX 的部分保存在 64 位浮点数之中,最长可能为 52 位。
因此,JavaScript 提供的有效数字最长为 53 个二进制位(64 位浮点的后 52 位 + 有效数字第一位的 1)。
3.2 复现:计算过程
返回目录
通过 JavaScript 计算 0.1 + 0.2 时,会发生什么?
1、 将 0.1 和 0.2 换成二进制表示:
0.1 -> 0.0001100110011001...(无限)
0.2 -> 0.0011001100110011...(无限
浮点数用二进制表达式是无穷的
2、 因为 IEEE 754 标准的 64 位双精度浮点数的小数部分最多支持 53 位二进制位,所以两者相加之后得到二进制为:
0.0100110011001100110011001100110011001100110011001100
因为浮点数小数位的限制,这个二进制数字被截断了,用这个二进制数转换成十进制,就成了 0.30000000000000004,从而在进行算数计算时产生误差。
3.3 扩展:数字安全
返回目录
在看完上面小数的计算不精确后,jsliang 觉得有必要再聊聊整数,因为整数同样存在一些问题:
console.log(19571992547450991);
// 19571992547450990
console.log(19571992547450991 === 19571992547450994);
// true
是不是很惊奇!
因为 JavaScript 中 Number 类型统一按浮点数处理,整数也不能逃避这个问题:
// 最大值
const MaxNumber = Math.pow(2, 53) - 1;
console.log(MaxNumber); // 9007199254740991
console.log(Number.MAX_SAFE_INTEGER); // 9007199254740991
// 最小值
const MinNumber = -(Math.pow(2, 53) - 1);
console.log(MinNumber); // -9007199254740991
console.log(Number.MIN_SAFE_INTEGER); // -9007199254740991
即整数的安全范围是: [-9007199254740991, 9007199254740991]。
超过这个范围的,就存在被舍去的精度问题。
当然,这个问题并不仅仅存在于 JavaScript 中,几乎所有采用了 IEEE-745 标准的编程语言,都会有这个问题,只不过在很多其他语言中已经封装好了方法来避免精度的问题。
- PHP Float 浮点型 - Manual
- Java 您的小数点到哪里去了? - Brian Goetz
而因为 JavaScript 是一门弱类型的语言,从设计思想上就没有对浮点数有个严格的数据类型,所以精度误差的问题就显得格外突出。
到此为止,我们可以看到 JavaScript 在处理数字类型的操作时,可能会产生一些问题。
事实上,工作中还真会有问题!
某天我处理了一个工作表格的计算,然后第二天被告知线上有问题,之后被产品小姐姐问话:
- 为什么小学生都能做出的小数计算,你们计算机算不了呢?
默哀三秒,产生上面的找到探索,最终找到下面的解决方案。
四 解决问题
返回目录
下面尝试通过各种方式来解决浮点数计算的问题。
4.1 toFixed()
返回目录
toFixed() 方法使用定点表示法来格式化一个数值。
- 《toFixed - MDN》
语法:numObj.toFixed(digits)
参数:digits。小数点后数字的个数;介于 0 到 20(包括)之间,实现环境可能支持更大范围。如果忽略该参数,则默认为 0。
const num = 12345.6789;
num.toFixed(); // '12346':进行四舍五入,不包括小数部分。
num.toFixed(1); // '12345.7':进行四舍五入,保留小数点后 1 个数字。
num.toFixed(6); // '12345.678900':保留小数点后 6 个数字,长度不足时用 0 填充。
(1.23e+20).toFixed(2); // 123000000000000000000.00 科学计数法变成正常数字类型
toFixed() 得出的结果是 String 类型,记得转换 Number 类型。
toFixed() 方法使用定点表示法来格式化一个数,会对结果进行四舍五入。
通过 toFixed() 我们可以解决一些问题:
原加减乘数:
console.log(1.0 - 0.9);
// 0.09999999999999998
console.log(0.3 / 0.1);
// 2.9999999999999996
console.log(9.7 * 100);
// 969.9999999999999
console.log(2.22 + 0.1);
// 2.3200000000000003
使用 toFixed():
// 公式:parseFloat((数学表达式).toFixed(digits));
// toFixed() 精度参数须在 0 与20 之间
parseFloat((1.0 - 0.9).toFixed(10));
// 0.1
parseFloat((0.3 / 0.1).toFixed(10));
// 3
parseFloat((9.7 * 100).toFixed(10));
// 970
parseFloat((2.22 + 0.1).toFixed(10));
// 2.32
那么,讲到这里,问题来了:
- parseFloat(1.005.toFixed(2))
会得到什么呢,你的反应是不是 1.01 ?
然而并不是,结果是:1。
这么说的话,enm...摔!o(╥﹏╥)o
toFixed() 被证明了也不是最保险的解决方式。
4.2 手写简易加减乘除
返回目录
既然 JavaScript 自带的方法不能自救,那么我们只能换个思路:
- 将 JavaScript 的小数部分转成字符串进行计算
/**
* @name 检测数据是否超限
* @param {Number} number
*/
const checkSafeNumber = (number) => {
if (number > Number.MAX_SAFE_INTEGER || number < Number.MIN_SAFE_INTEGER) {
console.log(`数字 ${number} 超限,请注意风险!`);
}
};
/**
* @name 修正数据
* @param {Number} number 需要修正的数字
* @param {Number} precision 端正的位数
*/
const revise = (number, precision = 12) => {
return +parseFloat(number.toPrecision(precision));
}
/**
* @name 获取小数点后面的长度
* @param {Number} 需要转换的数字
*/
const digitLength = (number) => {
return (number.toString().split('.')[1] || '').length;
};
/**
* @name 将数字的小数点去掉
* @param {Number} 需要转换的数字
*/
const floatToInt = (number) => {
return Number(number.toString().replace('.', ''));
};
/**
* @name 精度计算乘法
* @param {Number} arg1 乘数 1
* @param {Number} arg2 乘数 2
*/
const multiplication = (arg1, arg2) => {
const baseNum = digitLength(arg1) + digitLength(arg2);
const result = floatToInt(arg1) * floatToInt(arg2);
checkSafeNumber(result);
return result / Math.pow(10, baseNum);
// 整数安全范围内的两个整数进行除法是没问题的
// 如果有,证明给我看
};
console.log('------\n乘法:');
console.log(9.7 * 100); // 969.9999999999999
console.log(multiplication(9.7, 100)); // 970
console.log(0.01 * 0.07); // 0.0007000000000000001
console.log(multiplication(0.01, 0.07)); // 0.0007
console.log(1207.41 * 100); // 120741.00000000001
console.log(multiplication(1207.41, 100)); // 0.0007
/**
* @name 精度计算加法
* @description JavaScript 的加法结果存在误差,两个浮点数 0.1 + 0.2 !== 0.3,使用这方法能去除误差。
* @param {Number} arg1 加数 1
* @param {Number} arg2 加数 2
* @return arg1 + arg2
*/
const add = (arg1, arg2) => {
const baseNum = Math.pow(10, Math.max(digitLength(arg1), digitLength(arg2)));
return (multiplication(arg1, baseNum) + multiplication(arg2, baseNum)) / baseNum;
}
console.log('------\n加法:');
console.log(1.001 + 0.003); // 1.0039999999999998
console.log(add(1.001, 0.003)); // 1.004
console.log(3.001 + 0.07); // 3.0709999999999997
console.log(add(3.001, 0.07)); // 3.071
/**
* @name 精度计算减法
* @param {Number} arg1 减数 1
* @param {Number} arg2 减数 2
*/
const subtraction = (arg1, arg2) => {
const baseNum = Math.pow(10, Math.max(digitLength(arg1), digitLength(arg2)));
return (multiplication(arg1, baseNum) - multiplication(arg2, baseNum)) / baseNum;
};
console.log('------\n减法:');
console.log(0.3 - 0.1); // 0.19999999999999998
console.log(subtraction(0.3, 0.1)); // 0.2
/**
* @name 精度计算除法
* @param {Number} arg1 除数 1
* @param {Number} arg2 除数 2
*/
const division = (arg1, arg2) => {
const baseNum = Math.pow(10, Math.max(digitLength(arg1), digitLength(arg2)));
return multiplication(arg1, baseNum) / multiplication(arg2, baseNum);
};
console.log('------\n除法:');
console.log(0.3 / 0.1); // 2.9999999999999996
console.log(division(0.3, 0.1)); // 3
console.log(1.21 / 1.1); // 1.0999999999999999
console.log(division(1.21, 1.1)); // 1.1
console.log(1.02 / 1.1); // 0.9272727272727272
console.log(division(1.02, 1.1)); // 数字 9272727272727272 超限,请注意风险!0.9272727272727272
console.log(1207.41 / 100); // 12.074100000000001
console.log(division(1207.41, 100)); // 12.0741
/**
* @name 按指定位数四舍五入
* @param {Number} number 需要取舍的数字
* @param {Number} ratio 精确到多少位小数
*/
const round = (number, ratio) => {
const baseNum = Math.pow(10, ratio);
return division(Math.round(multiplication(number, baseNum)), baseNum);
// Math.round() 进行小数点后一位四舍五入是否有问题,如果有,请证明出来
// https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/Math/round
}
console.log('------\n四舍五入:');
console.log(0.105.toFixed(2)); // '0.10'
console.log(round(0.105, 2)); // 0.11
console.log(1.335.toFixed(2)); // '1.33'
console.log(round(1.335, 2)); // 1.34
console.log(-round(2.5, 0)); // -3
console.log(-round(20.51, 0)); // -21
在这份代码中,我们先通过石锤乘法的计算,通过将数字转成整数进行计算,从而产生了 安全 的数据。
JavaScript 整数运算会不会出问题呢?
乘法计算好后,假设乘法已经没问题,然后通过乘法推出 加法、减法 以及 除法 这三则运算。
最后,通过乘法和除法做出四舍五入的规则。
JavaScript Math.round() 产生的数字会不会有问题呢、
这样,我们就搞定了两个数的加减乘除和四舍五入(保留指定的长度),那么,里面会不会有问题呢?
如果有,请例举出来。
如果没有,那么你能不能依据上面两个数的加减乘除,实现三个数甚至多个数的加减乘除?
五 现成框架
返回目录
这么重要的计算,如果自己写的话你总会感觉惶惶不安,感觉充满着危机。
所以很多时候,我们可以使用大佬们写好的 JavaScript 计算库,因为这些问题大佬已经帮我们进行了大量的测试了,大大减少了我们手写存在的问题,所以我们可以调用别人写好的类库。
下面推荐几款不错的类库:
- Math.js。
Math.js 是一个用于 JavaScript 和 Node.js 的扩展数学库。
它具有支持符号计算的灵活表达式解析器,大量内置函数和常量,并提供了集成的解决方案来处理不同的数据类型,例如数字,大数,复数,分数,单位和矩阵。
强大且易于使用。
- decimal.js
JavaScript 的任意精度的十进制类型。
- big.js
一个小型,快速,易于使用的库,用于任意精度的十进制算术运算。
- bignumber.js
一个用于任意精度算术的 JavaScript 库。
最后的最后,值得一提的是:如果对数字的计算非常严格,或许你可以将参数丢给后端,让后端进行计算,再返回给你结果。
例如涉及到比特币、商城商品价格等的计算~