9.动态规划（2）——子集和问题

注：因为对“子集和问题”的学习不够深入，所以本文在讲解动态规划递推公式中可能存在叙述不清，或者错误的地方，如有发现望能不吝赐教。

　　子集和问题可描述如下：给定n个正整数W=(w₁, w₂, …, w_n)和正整数M，要求寻找这样一个子集I⊆{1, 2, 3, ..., n},使得∑wi=M,i∈I^[1]。举个例子对子集和问题做一个通俗的解释：集合W=(1, 2, 3, 4, 5)，给定一个正整数M=5，是否存在W的一个子集I，使得子集I中的元素相加等于M，这个例子显然存在子集I=(2, 3)。

　　问题定义：正整数集合S=(w1, w2, w3, …，wn)，给定正整数W，s[i, j]中的i表示S的一个子集，j表示子集i的和。如果S的某个集合i元素之和j=M，即问题有解。

　　举例：S=(7, 34, 4, 12, 5, 3)，W=6，是否存在S的一个子集，它的元素之和等于W。

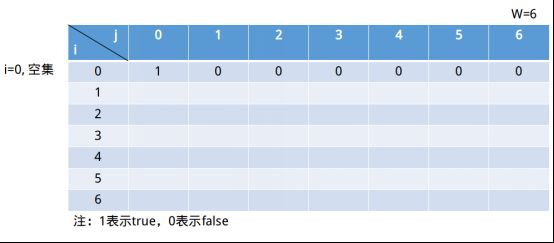
　　这个问题同样有多种解法，在本文中利用动态规划的思想进行求解，那么就需要推导出一个递推公式。我们将集合S不断的划分为小的集合，这就是动态规划的第一步：定义子问题。集合S最小的集合就是空集，空集当然不存在它的元素之和等于W，当然若j=0的情况下空集是符合条件的。

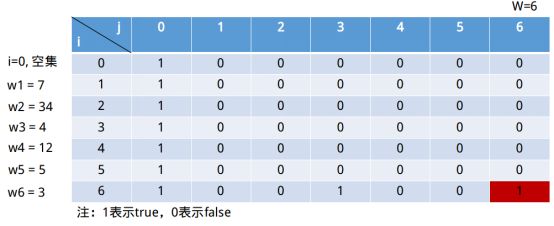
　　这个表格的列代表的是集合中的元素之和，最多只到达元素W，大于W当然没意义了。只要在j=6列中出现1，即得到问题的解。行表示前i个（包括i）元素组成的子集（这句话可能会有点疑问，这样岂不是扫描不到所有情况吗？接着往下看）。i=0表示为空集。

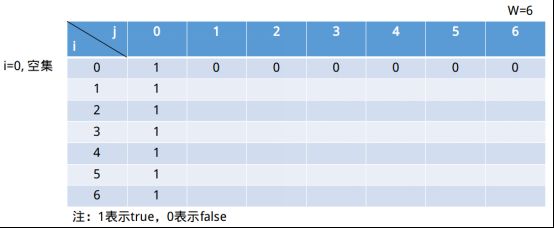
　　我们定义了j=6时，空集情况为true。那么当j=0时，这样对任意子集和都成立（空集是它们的子集）。所以表格继续填充如下图所示。

　　这些实际上是动态规划的第三步：定义初始状态。状态规划第二步则是定义状态转移规则，即状态之间的递推关系。

　　s[i, j]中的i表示的是前i个子集(包括i)。实际上我们从这里进行划分为两部分：

　　　　1)不包括第i个元素的前i个子集，即s[i - 1, j]；

　　　　2)包括第i个元素的前i个子集。
　　对于第1)种情况较易理解，前i - 1个集合元素之和等于j，那么前i个集合元素就存在子集元素之和等于j。

　　难于理解的是第2)种情况。对于第二种情况能明确一点就是s[i, X]中的i是确定的，关键是j，j此时如何定义？利用数学中的“特值法”，举例集合(3, 34, 9)，是否存在给定子集的元素之和等于37，此时i=2（子集为(3, 34)），j = 37，此时“包括第i个元素的前i个子集”这种情况下，s[2, 37] => s[2, 37 - 34] = s[2, 3]，子集(3, 34)当然存在它的子集元素之和等于3。那如果j = 36，s[2, 36] => s[2, 36 - 34] = s[2, 2]，子集(3, 34)显然不存在它的子集元素之和等于2。那j = 1呢，s[2, 1] => s[2, 1 - 34] = s[2, -32]，j - wi < 0，此时s[2, 1] => s[2 - 1, 1] = s[1, 1]，子集(3)显然不存在它的子集元素之和等于1。

　　综上，递推式如下所示：

　　在用代码实现这个算法前，先通过递推公式填写上面的矩阵。

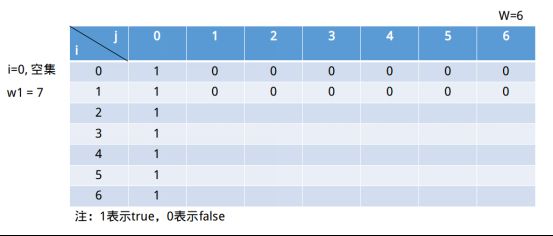
　　①i = 1, 此时子集为(7)，j = 1，j ∉ (∅)，选择情况2) => s[0, 1] || s[1, -6]（i = 0表示空集）。显然s[1, 1] = 0。

　　②i = 1，此时子集为(7)，j = 2，j ∉ (∅)，选择情况2) => s[0, 2] || s[1, -5]（i = 0表示空集）。显然s[1, 2] = 0。

　　……

　　⑥i = 1，此时子集为(7)，j = 6，j ∉ (∅)，选择情况2) => s[0, 6] || s[1, -1]（i = 0表示空集）。显然s[1, 6] = 0。

　　最后填充为如下图所示：

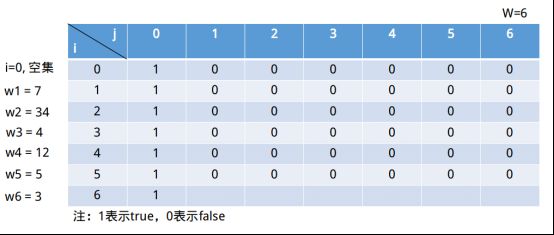
　　继续填充最后一行：　　

　　①i = 6, 此时子集为(7, 34, 4, 12, 5, 3)，j = 1，j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 1] || s[6, -2]（i = 0表示空集）。显然s[6, 1] = 0。

　　②i = 6, 此时子集为(7, 34, 4, 12, 5, 3)，j = 2，j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 1] || s[6, -1]（i = 0表示空集）。显然s[6, 2] = 0。

　　③i = 6, 此时子集为(7, 34, 4, 12, 5, 3)，j = 3，j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 1] || s[6, 0]。显然s[6, 3] = 1。

　　...

　　⑥i = 6, 此时子集为(7, 34, 4, 12, 5, 3), j = 6, j ∉ (7, 34, 4, 12, 5)，选择情况2) => s[5, 6] || s[6, 3]。显然s[6, 6] = 1。

　　Java

 1 package com.algorithm.dynamicprogramming;
 2 
 3 import java.util.Arrays;
 4 
 5 /**
 6  * 子集和问题
 7  * Created by yulinfeng on 7/2/17.
 8  */
 9 public class SubsetSumProblem {
10 
11     public static void main(String[] srgs) {
12         int[] sets = {7, 34, 4, 12, 5, 3};
13         int sum = 87;
14         boolean isExistSubSet = subsetSumProblem(sets, sum);
15         System.out.println("集合" + Arrays.toString(sets) + "是否存在子集的和等于" + sum + ":" + isExistSubSet);
16     }
17 
18     private static boolean subsetSumProblem(int[] sets, int sum) {
19         int row = sets.length + 1;
20         int col = sum + 1;
21         int[][] solutionMatrix = new int[row][col];
22         solutionMatrix[0][0] = 1;
23 
24         /**
25          *    0 1 2 3 4 5 6
26          * 0 |1|0|0|0|0|0|0|
27          * 1 |x|x|x|x|x|x|x|
28          * 2 |x|x|x|x|x|x|x|
29          * 3 |x|x|x|x|x|x|x|
30          * 3 |x|x|x|x|x|x|x|
31          * 4 |x|x|x|x|x|x|x|
32          * 5 |x|x|x|x|x|x|x|
33          * 6 |x|x|x|x|x|x|x|
34          */
35         for (int i = 1; i < col; i++) {
36             solutionMatrix[0][i] = 0;
37         }
38         /**
39          * 初始状态
40          *    0 1 2 3 4 5 6
41          * 0 |1|0|0|0|0|0|0|
42          * 1 |1|0|x|x|x|x|x|
43          * 2 |x|x|x|x|x|x|x|
44          * 3 |x|x|x|x|x|x|x|
45          * 3 |x|x|x|x|x|x|x|
46          * 4 |x|x|x|x|x|x|x|
47          * 5 |x|x|x|x|x|x|x|
48          * 6 |1|0|0|x|x|x|x|
49          * [i][0] = 1，按行填充
50          */
51         for (int i = 1; i < row; i++) {
52             solutionMatrix[i][0] = 1;
53             for (int j = 1; j < col; j++) {
54                 solutionMatrix[i][j] = solutionMatrix[i - 1][j];
55 
56                 if (solutionMatrix[i][j] == 1) {
57                     solutionMatrix[i][j] = solutionMatrix[i][j];
58                 } else if ( j - sets[i - 1] >= 0 && solutionMatrix[i][j - sets[i - 1]] == 1) {
59                     solutionMatrix[i][j] = solutionMatrix[i][j - sets[i - 1]];
60                 } else {
61                     solutionMatrix[i][j] = 0;
62                 }
63 
64                 if (j == col - 1 && solutionMatrix[i][j] == 1) {
65                     return true;
66                 }
67             }
68         }
69 
70         return false;
71     }
72 }

　　Python3

 1 def subset_sum_problem(sets, sum):
 2     row = len(sets) + 1
 3     col = sum + 1
 4     solutionMatrix = [[0 for c in range(col)] for r in range(row)]
 5     solutionMatrix[0][0] = 1
 6     for i in range(1, col):
 7         solutionMatrix[0][i] = 0
 8 
 9     for j in range(1, row):
10         solutionMatrix[j][0] = 1
11         for k in range(1, col):
12             solutionMatrix[j][k] = solutionMatrix[j - 1][k]
13             if solutionMatrix[j][k] == 1:
14                 solutionMatrix[j][k] = solutionMatrix[j][k]
15             elif (k - sets[j - 1] >= 0) and (solutionMatrix[j][k - sets[j - 1]] == 1):
16                 solutionMatrix[j][k] = solutionMatrix[j][k - sets[j - 1]]
17             else:
18                 solutionMatrix[j][k] = 0
19             if k == col - 1 and solutionMatrix[j][k] == 1:
20                 return True
21 
22     return False
23 
24 sets = [7, 34, 4, 12, 5, 3]
25 num = 6
26 is_exist = subset_sum_problem(sets, num)
27 print(is_exist)

 

---

[1]李肯立, 李庆华, 张红君. 子集和问题的改进算法[J]. 计算机科学, 2003, 30(11):16-17.

 

这是一个能给程序员加buff的公众号