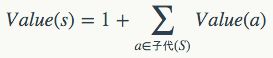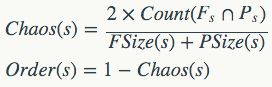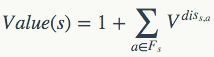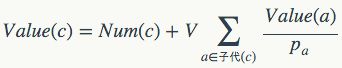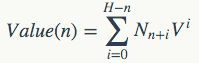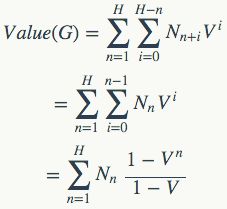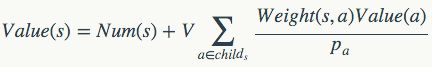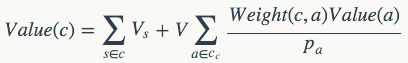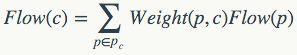这次开一个小脑洞。
因为是脑洞,所以是有水分的,很多定义是模糊的,推理过程也并不要求严格。
话题先从标题的最后一项开始说起。
什么是不可压缩信息?
这个具体可以看这篇文章,大意来说,便是在选定了通用图灵机后,可以用于生成指定字符串的所有图灵机中长度最短的图灵机的长度,就是指定字符串的K氏长度。而如果一个字符串的长度不大于它的K氏长度,那么这个字符串被称为“不可压缩”的。
因此,很显然,如果我们构造出一个集合S是“所有字符串构成的集合”,然后构造一个映射K,将S中的元素映射到其对应的不可压缩形式(即如果字符串A可以通过字符串B对应的图灵机来给出,而B的长度等于A的K氏长度,那么我们就说B是A的不可压缩形式),那么很显然S肯定存在一个子集U,U是S中所有不可压缩形式字符串的集合。
PS:当然我们这里不得不指出的是,上述所提到的K是不可计算的,也是不完备的,相关证明可以看上面所给的那篇参考文章。
U具有一个很美好的性质,便是U中任意两个字符串对应的图灵机都不可能生成相同的字符串。同时,U中的每个元素都可以代表S中的一个轨道,即S中所有那些与U中元素u生成相同字符串的字符串集{s},与u是一一对应的,且u就在{s}中。这样的字符串集{s}记为S(u)。因此很显然,对于任意ui和uj,S(ui)与S(uj)的交集都为空集,且所有S(u)的并等于S。
所幸这样的集合显然是离散的,否则我们可以很有兴趣地追问在这样的集合上是否存在塔斯基怪异分解……
从本质上来说,U中的元素都是无须输入的图灵机,所需的所有素材都包含于自身之中。
我们事实上可以定义s的“逻辑深度”,即如果u是s的不可压缩表示,那么从u开始执行,总共需要执行多少步才能最终停机并输出s,这个执行步骤数就是s的逻辑深度。
既然是图灵机,那么我们自然会考虑这么一个问题:这些图灵机之间是否存在一些逻辑上相似的结构呢?比如两个u采用了相同的逻辑,只不过其中部分常数的不同,导致了相同的逻辑输出了不同的结果。
基于这种想法,我们开始做一些不一样的尝试。
选择一组图灵机{Ti},其共同特点是以一个字符串作为输入,然后以一个字符串作为输出。
同时,这组图灵机可以实现对任意字符串集S的覆盖:对于任意S中的元素s,总存在S中的一个元素s'以及该图灵机集中的一个图灵机T,使得T(s')=s。
这样的图灵机集可以成为S上的一个图灵覆盖。
很显然,最平庸的这种图灵覆盖只需要一个图灵机,那便是“复写者”,将输入原封不动地作为输出。
有了上述覆盖后,我们可以重新定义“压缩”:
如果字符串s可以由图灵覆盖中的一组图灵机生成,即存在子集{Ti}使得s=Ti(si),那么这组si中长度最小的那个,称为s在图灵机覆盖{T}中的不可压缩表示,其长度称为s在覆盖{T}中的本征长度,对应的图灵机Ti为s的生成机——如果从同一个si可以通过多个图灵机生成s,那么就选择逻辑深度最浅的那个作为生成机;如果还有多个图灵机连逻辑深度都一样,那么就选择本身长度最短的。这样得到的二元组
很显然,与上面一段定义的K氏长度只依赖于通用图灵机的选择(而且只依赖到差一个常数长度差的程度)截然不同,这里的不可压缩形式以及不可压缩长度在很大程度上都依赖于图灵覆盖的选择——或者我们也可以这么说,当图灵覆盖是所有可能的图灵机构成的集合时,上述定义就回归到了K氏复杂度的情况中了。而,与此同时,由于可选的图灵机由图灵覆盖给定,而我们可以选择一个有限的或者无限但足够特殊的图灵覆盖,使任意字符串的不可压缩表示以及本征长度都是可计算的。这也是现在这个系统与K氏复杂度问题的最大不同之处。
PS:事实上,这种处理方案只要确保图灵覆盖本身不构成自指即可。当我们选择“所有可能的图灵机”作为图灵覆盖时,总是可以构造一个特定的图灵机,它可以通过“所有可能的图灵机”来引用自身,从而构成自指结构,但这样的过程在选择图灵覆盖可以选择和控制时就可以有效避免。
现在,对S做一个恰当的弱化——S不再是所有字符串构成的集合,而是一个任意的字符串集。对于非所有字符串构成的集合S,图灵覆盖的要求就比之前的要严格,一般而言“复述者”图灵机总是存在的,这样才能确保S中的每个字符串都能有不可压缩表示。
S中的任意字符串s都可以分解为一个不可压缩表示与生成机这两个元素构成的一个二元组[ws,ts],其中ws为s的不可压缩表示(也是一个字符串),而ts则是图灵机覆盖集中的一个图灵机,也就是s的生成机。这种形式的分解是唯一的,即对于任意s,只有唯一的二元组[ws,ts]与之匹配。
因此,S被分解为了若干子集St,每个子集的任意元素s,都可以写成[ws,t]的形式,其中t就是该子集的特征生成机。这些子集之间彼此没有交集,这是由定义所保证的。
又由于每个子集St中的元素s都可以写成[ws,t]的形式,从而显然集合{ws}是St的不可压缩表示,前者可以通过生成机t生成后者,后者每个元素的不可压缩表示构成的集合便是前者。
而,一个有趣的问题就出现了:不同的St之间虽然没有交集,但它们的不可压缩表示集之间却是可以有交集的——同一个w,在两个不同的图灵机的作用下,是可以生成两个不同的字符串s的。
进一步来说,这里的问题实质上是这样的:
字符串a通过图灵机t生成了字符串b,即b=t(a),而后b通过图灵机r生成了字符串c,即c=r(b),那么我们当然有c=r(t(a))。但,如果联合函数r·t并不是图灵机覆盖集{T}的元素的话,那么虽然c=r(t(a)),但a依然不能直接生成c,从而a不是c的不可压缩表示。
从图的角度来说,a与b之间存在最短连线,b与c之间也存在最短连线,而a与c的距离最短,但却不存在连线将a与c直接相连,那么此时即便a比b更接近c,c的最近相连的邻点也只能是b而不是c。
因此,现在我们有了一个很有趣的局面:S的不可压缩表示未必在S内,且两个相交为空的字符集的不可压缩表示可以相交。
进一步,如果选择恰当的图灵覆盖,那么可能产生这样的局面:字符串S的不可压缩表示为s1,而s1的不可压缩表示为s2,且s1不等于s2。这样的链条可以一直进行下去,直到出现某个字符串的不可压缩表示在链条内出现过为止。这样的链条被称为压缩链,而链条的长度就被称为一个字符串的压缩深度,而链条的第n+1位(这里原字符串被设为链条的第一位)称为字符串的第n层压缩。同时,从全局来看,逻辑深度最深的节点的逻辑深度,成为整张图S的逻辑深度,记为DeepS。
PS:这里有一个很有趣的问题,就是我们对于压缩链的停止的定义为:直到出现某个字符串的不可压缩表示在链条内出现过为止,这其实就是说,存在这么一种情况,某个字符串的不可压缩表示是它自己,或者在若干次压缩后,回到了自己。比如s0的不可压缩表示是s1,而s0的不可压缩表示是s2,s2的不可压缩表示却是s0。由于现在压缩的本质是利用图灵覆盖中的图灵机从一个字符串来生成指定字符串,因此不排除这种循环的情况出现。这也表示一点:在特殊选择的图灵覆盖下,字符串s的不可压缩表示,是有可能比s自身还要长的,尤其当图灵覆盖中不包含复述者图灵机的时候。
以此为基础,当我们选定字符集S和图灵覆盖{T}后,我们当然可以找出S中所有压缩深度为1的字符串,记为RootS,而所有别的字符串都可以通过一条压缩链从RootS中派生出去。
我们可以脑补一下,当我们选择一个“所有可能的且不含有自指结构的图灵机”作为图灵覆盖的时候,那么很可能所有字符串就都是压缩深度为1的Root节点了。因此,Root的分布与S和{T}的选择是密切相关的,那么到底能有多相关呢?
由于现在一个字符串可能通过若干个生成机成为若干个字符串的不可压缩表示,所以很显然的是,上述压缩链在某些节点上必然会合并到一起,从而整条压缩链及其所有与之相连的压缩链在形式上构成了一种树状结构——压缩树。而图G中所有压缩树就构成了G的压缩林。
这也就是说,如果定义“a的不可压缩表示是b”的逆关系为b“最简生成”a,那么我们就可以定义字符串s的“子代”为所有s最简生成的字符串的集合,而s就成为所有这些子代的“父节点”,当然也就是它们的不可压缩表示了。显然子代和压缩链是逆关系。
接着,就如压缩链的终点是Root集,总会存在一些字符串的子代为空集,这些字符串便构成了S上的叶节点集,记为LeafS。而非Leaf的节点则可以定义其宽度,为其子代的元素数,从而叶节点就是宽度为零的节点。
因此,现在随着不可压缩表示而来的,就是压缩链与子代,以及深度与宽度,Root和Leaf。
在上述结构下,一个很有趣的问题是:到底哪些节点更“重要”?
虽然Root生成了整张图,但若论重要性,Root却未必是最重要的那些节点——一个Root节点被移除后,其子代完全有可能被别的节点给生成出来,那么这个Root节点的重要性就非常有限了。
比如整张图中最宽的节点,如果它被去掉,那么就可能导致大量节点的深度被迫加深,甚至于可能使得整张图断裂(即存在不连通的至少两个区域,参考这篇文章)。但,最宽的节点却未必是最重要的,比如图上一个最宽的节点的所有子代都是Leaf,那么这个节点本身的重要性就很有限了。
那么,如何定义这个重要性就成了一个很关键的问题。
这里,先来定义一个节点的“价值”:
这样定义的价值可以分解为两部分:节点自身的价值,以及节点从子代身上继承而来的价值。因此,一个节点的重要性不单单在于它自己作为一个字符串而体现出的价值,更表现在它可以派生出的节点的价值上。一个节点自身可能没什么重要的,但是它所派生出去的那些分支却可能非常重要,从而也就能体现出它本身的重要性来。
而,很显然的,Leaf的价值永远只有1。
在上式中我们可以给从子代继承而来的部分乘上一个合理的介于0到1之间的常值系数即“ 继承因子”,从而调节继承的作用:
因为可想而知,如果这个系数为1,也就是现在所定义的这样,那么Leaf的价值将被它所在的整条压缩链上的每个节点所继承,那么这个Leaf的逻辑深度越深,它的实际贡献也就越大。但这点本身却未必合理,因为这将导致一个逻辑深度很浅的多个Branch交汇的节点的价值没有一个逻辑深度很深的Leaf的价值高,这有点不合常理。
因此,我们这里暂时将V设为0.5,这样一个Leaf的逻辑深度再深,影响也将是有限的。
从另一个角度来说,一个节点的价值有一部分是继承自其子代的,因此如果这个集成系数为1的话,就表示它的 子系(所有包含该节点的压缩链上该节点之后的所有节点构成的集合)的每个节点都为它做出了贡献,这样的节点显然越靠近Root就越有价值,但这点并不合理,因为这些节点本身可能仅仅支持起到了一个“传递者”的作用——它们的宽度都只有1,从而只是将上一个节点连接到下一个节点而已。这样的节点理应是不重要的,但在继承因子为1的时候,却可能变得很有价值起来。因此,选择一个小于1的继承因子是非常重要的。
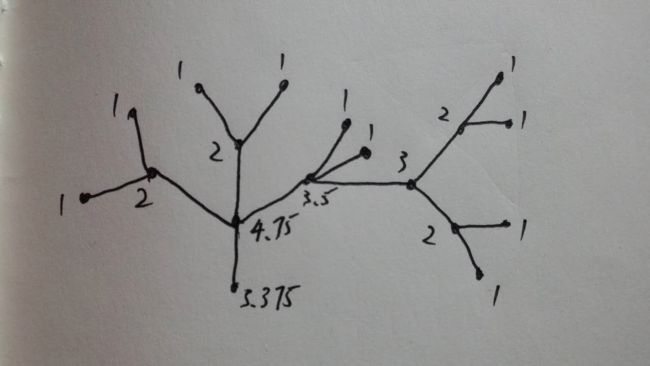
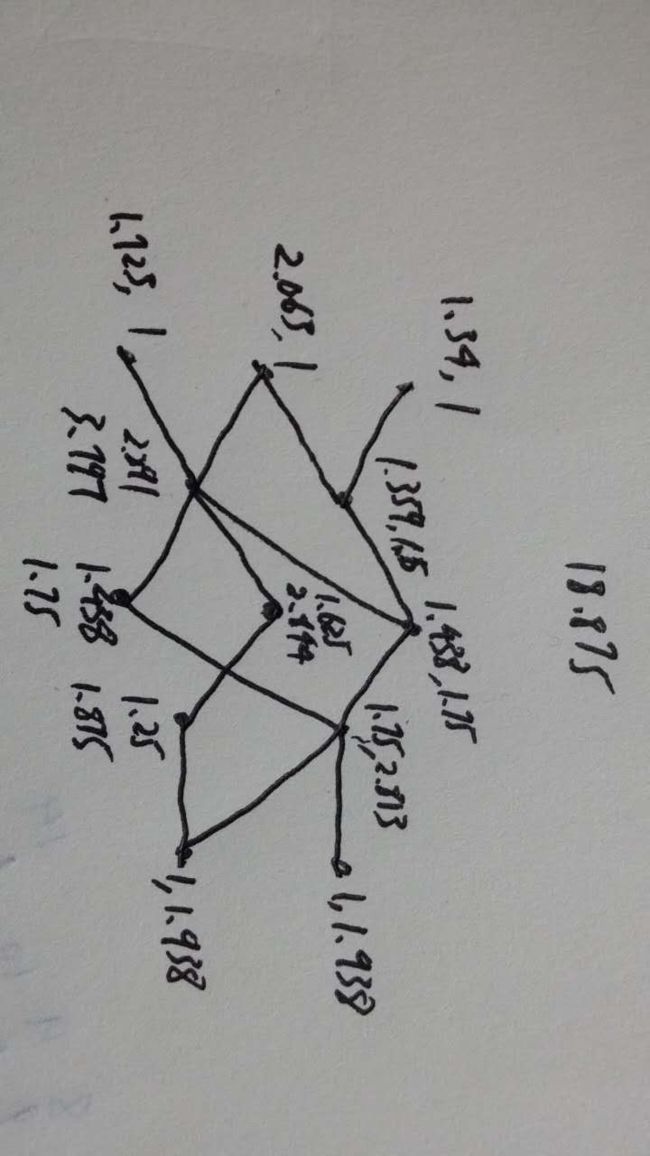
比如下面这张图:
可以看到,这里价值最高的节点是主干顶端分叉五个Branch出去的那个节点,这也和我们直觉的理解相吻合。
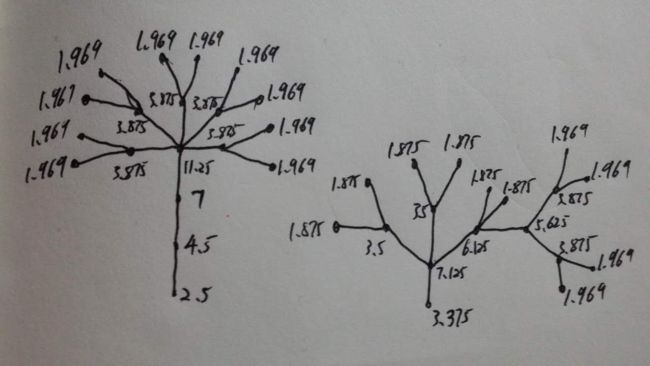
下面再看另一张图:
在这张图中,每个节点的价值也基本是符合我们的直觉预期的,其中最重要的点分别是Root、逻辑深度为1的三个Branch交汇的节点、右侧两个Leaf一个Branch交汇的节点、以及该节点之后的两个Branch交汇的节点,其中后三个的重要性不言而喻。
通过这两个例子,不难发现,这样定义的节点的价值与重要性之间,还是比较匹配的,但总还是有些偏差,因此下面我们引入另一个更重要的指标:节点的 影响力。
要计算节点的影响力,我们先来计算一下整张图G的总价值,其定义相当直白:
也即,图G的总价值,就是图中所有节点的价值的总和。比如说,上面两张图的总价值就分别是35.5和32.625。
接着,我们考虑将G中的某个节点移除的话,会得到什么样的图。
由于G中的节点之间的连线是通过不可压缩表示来给出的,如果一个节点被移除的话,那么对于它的父节点而言,无非就是这个不可压缩表示被取消了,但对于它的子节点而言情况就比较复杂了,因为这个节点被移除,无非就是表示原本的不可压缩表示关系被取消,但节点依然可以有别的不可压缩表示。因此,对于被移除节点s的子节点,现在可能是别的节点的最简表示,也可能不是任何节点的最简表示从而变为Root节点。
因此,原图G中一个节点s被移除后,其对应的压缩林相对于原始的压缩林,所出现的就是s的部分子节点变成了Root,而部分子节点所处的Branch则整个被嫁接到了别的节点上。
从而,我们自然可以计算这么一个问题:G的压缩林的总价值,和G被移除节点s后的压缩林的总价值,它们的该变量是多少?
这个该变量便被定义为节点s的“ 影响力”:
因此,一个节点真正的“价值”,就体现为有它和没有它为整个体系所带来的改变。
比如,上面的那两张图,现在可以分别求出所有点的影响力为:
可以发现,这里影响力的分布与价值的分布基本是相匹配的,在某些节点(比如第二张图的Root节点)上比只看价值更好。
同时,我们也可以发现一件有趣的实——去掉节点s后的图,相对原来的图,其总价值未必始终是减少的。存在这么一种可能性,s的子代由于s的消失,集体被嫁接到了另一个或者另一批节点上,反而使得新图的总价值升高。这样的情况在复杂的图中是有可能出现的,我们会在后面进行分析。
对于这样的负影响力的节点,一般表示它肯定可以被“更恰当”地归类为别的节点的最简生成。比如通过添加图灵机的方式修改图灵覆盖,那么就可能达到这样的目的。
这同时也表明了:连接两个节点的连线l,现在也是可以判断其影响力的:
只不过,我们可以知道,压缩林中图灵覆盖里的一台图灵机t所对应的,并不只是图中的一条边,而可能是一组边,从而在可以赋予每条边一个影响力的同时,也可以通过移除一个图灵机t来计算出t的影响力。
从而现在图G中的每个节点和每条边都被赋予了一个影响力值,而字符串集与图灵覆盖中的每个字符串与图灵机,也被赋予了一个价值。
虽然我们已经有了一张图
这就是下一个问题了——
在之前的一段中,我们通过给定图灵覆盖后的不可压缩表示来构造连接两个字符串的关系,使得一个是另一个的不可压缩表示,而反过来后者是前者的最简生成。这样的关系沿着不可压缩表示可以建立一条压缩链,而反过来则可以给出一棵子代树,从而整个空间
但,我们都知道,不可压缩表示是两个字符串节点的所有可能关系中最“密切”的一种关系,从而限制性很大。我们现在来寻求比压缩林更丰富的结构。
容易知道,任何一个字符串s都可能有这么两类“亲属”。
第一类亲属,其中的元素都可以通过图灵覆盖中的某台图灵机来生成s,称为s的父代;而另一类亲属的元素则都可以由s通过图灵覆盖中的某台图灵机来生成,成为s的子代。
由于图灵覆盖中的图灵机只要求以一个字符串为输入然后输出一个字符串,但并不要求对于任意字符串都可以接受并停机且有输出,从而这里的图灵机实际上是S上的一个偏函数而非函数,因此就存在一些字符串不能作为特定图灵机的输入,甚至于一些字符串不能成为图灵覆盖中任何一台图灵机的输入。
因此,现在我们实际上就可以通过生成与被生成的关系,而非之前不可压缩表示与最简生成的关系,来构造出一个全新的网络结构——生成云。
生成云显然是有向图,且和压缩林不同,生成云不是林状的,而是网状的。
压缩林的任意两棵树之间没有交集,甚至同一个节点派生出的两个Branch之间也是没有交集的,且任意节点都只有唯一一个父节点。但生成云中一个节点可能是若干个节点的子节点,也可以是若干个节点的父节点。
一个节点在压缩林中的父代必然是其在生成云中的父代,而它在压缩林中的子代也必然是其在生成云中的子代,反之则未必。
在定义了生成云后,我们可以定义“生成链”,类似于压缩林中的压缩链。生成链也是有向的,从字符串a指向字符串b,且a为生成链的第一个元素,b为最后一个元素,a可以通过某台图灵机生成下一个元素,然后再通过某台图灵机生成第三个元素,直到生成b为止。因此一条生成链的两个元素节点之间通过一台图灵机相连,而两根生成链即便元素节点全同,也可以是不同的生成链,因为连接两相邻节点的图灵机可以不同,这是生成链与压缩链最大的不同,因为压缩链中相邻元素之间的生成机是唯一的。
这同时也就说明,如果b是由a生成的,那么从a到b的连线可以不止一条,因为可以有不止一台图灵覆盖中的图灵机由a生成b。
生成链的节点数(不考虑连接两相邻字符串节点的图灵机)称为生成链的长度,而其图灵机在生成过程中的总逻辑步骤数称为该生成链的逻辑深度。
接下来,定义从a到b的所有生成链中长度最短的那条生成链的长度减1(从而也就是生成链中的图灵机的数量),为从a到b的有向距离(也可以简称为从a到b的距离),记为da,b;而从a到b的所有生成链中逻辑深度最短的生成链的逻辑深度,为从a到b的逻辑距离,记为Da,b。显然,从a到b的有向距离距离对应的生成链与逻辑距离对应的生成链,未必是同一根生成链。
PS:这种有趣的情况不由地让人想到了Finsler流形上,“直线”(自平行曲线)与“最短线”(长度极值曲线)可以不是同一根线这么一个很奇妙的情况。
值得注意的是,未必一定存在一根生成链连接指定的字符串a与b,在这种情况下,称从a到b是不相连的或者断裂的,其有向距离与逻辑距离都为无穷大。而从a到b是断裂的,未必从b到a就一定也是断裂的。
显然,字符串s的父代到s的距离必然是1,但反过来,s到它的父代的距离则未必是1,有时候甚至可能是断裂的。
继续参考压缩林,我们当然会去思考关于生成云中Root与Leaf是否存在这样的问题,但压缩林中由于不可压缩表示的约束非常强,以至于任意一张这样的图
我们可以定义不能作为任何一台图灵机的输入的字符串为生成云中的Leaf,但这对于图灵覆盖的选择就有了一定的要求,因为比如只要给图灵覆盖一个可以将任意字符串作为输入的图灵机,那么这样的Leaf就不存在了——但这却不会使得压缩林中的Leaf消失。
我们当然也可以直接将压缩林中的Root与Leaf作为生成云中的Root与Leaf来用,但这样的做法不免太过人为与强制,并没有什么深刻的意义。
可以说,生成云与压缩林另一个重要的不同,就是两者虽然都是有向图,但生成云几乎无法定义一个明确的层级结构,而压缩林在这方面的结构却是非常显而易见。
我们当然也希望可以计算生成云中每个节点的重要程度,比如压缩林中的价值与影响力,总是希望可以找到其在生成云中的对应的。但由于现在一个节点的子代可能与其父代重叠,因此压缩林中定义价值时的迭代定义的方式就会遭遇自己求和自己的困境。
为此,我们先来看子代与父代的推广。
前面我们已经给出了节点之间生成链的定义,这里就可以利用生成链来给出一个节点的两个重要的“领域”——
所有存在一根生成链从节点s连接到其的除了s自身的节点构成的集合,称为s的影响域,记为Fs。而所有存在一根生成链从其连接到s的除了s自身的节点构成的集合,称为s的被影响域,记为Ps。定义中强调了“除了s自身”,是因为s本身可以和自身相连,从而自己通过有限步生生自己,故而在影响域与被影响域的定义中要扣除s自身,所以本质上这两个都是去心域。在一个足够混乱的生成云中,节点的这两个域可以全等。
在这两个域中,我们都可以定义其“大小”与“深度”:用FSize表示Fs的元素个数,而用PSize表示Ps中的元素个数。而FDeep表示s到Fs中元素的有向距离的最大值,而PDeep表示Ps中元素到s的有向距离的最大值。
接着,我们可以利用F和P来定义节点s的“混乱度”与“有序度”:
因此,很显然压缩林的混乱度为0有序度为1,但在生成云中则未必,说不定会很接近于混乱度为1的状态。
如果一张图的每个节点的有序度都为1,那么就称这张图为 全序图。显然压缩林就是一张全序图。
之所以要定义节点s的影响域,就在于压缩林中的价值的定义,可以被用影响域等价地定义出来:
这里V就是之前在压缩林中所定义的继承因子,一般选为0.5。
由于我们利用有向距离来作为计算因子,而两个节点之间的有向距离是唯一的定值,所以这样的定义方式可以有效地避免此前提到的价值与影响力计算中可能出现不断指向自己的麻烦。
但直接套用上式来计算生成云节点的价值却是不合适的,会得到很多奇怪的反直觉的结论。其根本在于,压缩林中任意节点的父元素只有一个(除了Root没有父元素),但在生成云中这点却是未必。因此,我们需要对上面的定义做出修改,并且可以直觉地给出如下形式的结果:
其中p s表示节点s的父元素的数量(相应的c s就是s的子元素的数量了。
但这样的定义依然是有一定问题的,因为随着连接结构的日趋复杂,简单地将一个节点的“共享”分摊到父节点上一次来作为统计中的计算项显然会无法符合要求,我们需要更加有力的工具。
在前面生成云的问题中,我们最核心的难点有两个:
- 无法简单地给出生成与被生成的关系,因为一个节点的影响域与被影响域可能重叠,从而自己可以通过图灵覆盖中的图灵机的迭代作用生成自己,这就导致了生成与被生成关系的混乱不清。
- 由于父节点的非唯一性,简单统计父节点数也是无法满足需求的。
第一个问题使得我们无法使用迭代的方式求节点的价值,因为那样会无限迭代到自身;而第二个问题使得我们无法使用简单加权求和的方式来求节点价值,因为父级结构将无法被考虑在内。
为此,我们需要一种全新的工具——有别于压缩林,可以更好地反映生成云,但同时又比生成云简洁,最好可以给出类似压缩林那样的明确的层级结构。
为此,下面将在生成云上引入一种等价关系,并利用这种等价关系将生成云简化为拥有良好层级结构的新的有向图:等价网。
我们都知道,生成云中连接两个节点的,是两个节点a与b之间的生成关系——如果存在图灵覆盖{T}中的图灵机t使得b=t(a),那么就说a可以生成b。
那么,让我们来考虑这么一个问题:假如a可以生成b,而b又可以生成a,那么这两个节点之间会是一种什么样的关系?是不是可以认为a和b“足够相似”?
因此,我们引入一种“等价关系”:
如果存在从a到b的生成链,同时也存在从b到a的生成链,则称a和b等价。
所有与a等价的节点构成了a的等价类,而且如果考虑这个等价类作为集合配上当前图的图灵覆盖,那么生成的这张生成云子图很显然具有1的混乱度即0的有序度。
很显然,等价类C中任意节点s的等价类都必然是C自身。
进一步,让我们来定义两个等价类之间的生成与被生成的关系:
如果存在等价类A中的节点a与等价类B中的节点b,且满足a生成b,那么我们就说等价类A生成等价类B。
很显然,在两个等价类之间的生成关系必然是单向的,即当A生成B的同时,不可能存在A中的节点c与B中的节点d使得d生成c这个关系成立,因为如果这样的关系存在,那么B中任意节点必然可以通过一条生成链进入A中,然后再回到B中最后终结于自己,从而A和B这两个等价类等价。
有了这样的等价关系后,原来的图G中的节点的关系就可以被大幅地简化。
我们用等价类取代G中的节点,从而构造出一个图G模掉等价关系后的等价图G',进而考虑G'的生成云,它被称为原图G的“等价网”。
等价网中任意两个节点之间要么没有有向箭头连接,要么只有一根单向的箭头连接,而且更重要的是,任意节点的被影响域与影响域没有交集,从而是一张全序图。
既然是全序的,那么我们自然可以找到两类节点,一类节点不被任何别的节点生成,即为Root节点,而另一类节点则不生成任何别的节点,即为Leaf节点。这点与压缩林中的情况完全相同。
Root节点到任意一个指定节点的有向距离的最小值(因为等价网本身是生成云,所以生成云中的定义在等价网中可以直接使用),被称为该节点的逻辑深度,而它到Leaf节点的有向距离的最小值则被称为逻辑浅度(实在不知道叫什么名字好了……),而不同Leaf节点的逻辑深度可能不同,不同Root节点的逻辑浅度也可能不同。Root节点的浅度的最大值,同时也是Leaf节点深度的最大值,被称为等价网的厚度H。
将逻辑深度相等都为n的节点构成的集合称为等价网的等高面n,那么我们可以发现,逻辑深度为n的节点可以生成的点,未必都坐落在等高面n+1上,它既可以生成等高面n上的点,也可以生成等高面n+1上的点,或者等高面n-1上的点,甚至别的各层上的点。等价关系只能保证任意生成链不自相交,任意节点的影响域与被影响域不相交,却无法保证任意生成链只能从低等高面往高等高面延伸。
接下来,我们来构造等价网上节点的价值:
其中,Num(c)给出了节点等价类c中的元素数。和压缩林中的情况一样,我们现在又可以使用迭代的方式来定义节点的价值了——这边是全序网的一大优点。
接着,通过和压缩林中相同的方式,我们可以定义整个等价网的总价值,进而给出每个节点(包括每个等价类的价值和每个原图G中节点的价值)、每条边、每台图灵机的影响力。
如此一来,通过等价网,我们终于完成了在生成云中无法实现的计算。只不过现在价值的计算还算简单,但影响力的计算,就要求在计算每个G中节点的影响力的时候,重新生成等价网,从而在实际情况中的计算量是非常巨大的。
可以看出,由于图灵覆盖的特殊性,完全可能存在这样的情况,即在生成云中同属同一个等价类的不同节点,有些在移除后对整个等价网完全不构成形变,而有些则可能使得等价类中的节点彼此之间不再等价,而有些则可能使得不同等价类之间的链接关系发生改变。
显然,第一类节点(完全不改变等价网)虽然和别的几类节点共享相同的价值,但影响力却是微乎其微的;而第二类节点则对等价网整体的改变最显著,将一个等价类完全拆散了,从而具有极大的影响力;第三类节点则还算是较普通的情况,与压缩林中的节点拥有相同的行为特性。
当然,等价网也是可以有一些压缩林中所几乎不会拥有的性质的。比如,我们可以讨论一个节点的“不可替代度”。
不可替代度可以被视为反映一个节点不可替代性的标准,而为了获得唯一性,我们需要介绍节点s的影响域中一个非常重要的子集——
如果以节点a为终点的所有生成链都必然还有节点s,那么就称a为s的专属子节点。s的所有专属子节点构成了s的专属子域Us。
容易证明,s的专属子节点的子节点未必依然是s的专属子节点,但s的专属子节点的父节点则必然是s的专属子节点。
从而,节点s的不可替代度U(s)就是s的专属子域节点数与全网节点数的比。
很显然,不可替代度越高的节点,在整个网中的重要性是不言而喻地重要的。它的缺失将导致整个网络的极大改变。
我们可以计算s及其专属子域的总价值以及总影响力——后者的计算是将s与Us的所有节点全部移除后的图的总价值与原图总价值的差——它们被称为s的不可替代价值与不可替代影响力。
在压缩林中,一个节点的专属子域就是它的子元素为开端的所有Branch的总和,所以显然Root的不可替代影响力是无与伦比的。但在生成云与等价网中,情况就完全不是这样了,变得非常扑朔迷离。
至此,通过等价关系的引入从而从图G中构造出等价网并利用登记网来计算原图G中生成云中节点的价值与影响力的方案,就算告一段落了。
这部分我们先做一些简单的计算。
我们知道,在压缩林中节点的价值被定义为:
从而可以被等价地从迭代形式改写为求和形式:
现在我们对等高面n(以下记为L n)上的价值求和,由于压缩林中不同节点的影响域无交集,以及从L n到其距离为1的节点必然都落在L n+1上,从而这个求和可以直接给出非常简洁的形式:
其中N n表示L n上的节点数。这么一来图G的总价值也就很好计算了:
也就是说,总价值等于每一层节点数的加权总和,而权重就是(1-V n)/(1-V)(当然如果V取1的话就是n)。
从这里也可以看出,逻辑深度越深的节点,对整张图总价值的作用当然是越大。
当一个节点被从图中移除后,假如说不改变每一层的节点数,比如它的所有子节点都被从一等高面上的别的点继承,那么除了该节点所在等高面上的节点少了一个,别的等高面上的节点数不便,那么新图和旧图之间的总价值差就只是这个等高面n上的统一权重因子。
事实上,逻辑深度为n的节点s的影响力现在已经可以做这样的简化计算了:
其中m a是s影响域内节点a原来的逻辑深度,而m' a是随着s的被移除而改变位置后的逻辑深度。
由此可以看出,对于节点自身的被移除来说,n越大,影响力越大;而考虑上s的影响域中的节点后,由于V是小于1的正数,所以越往深度浅的层走的话会为节点s贡献正的影响力。
因此,假如一个节点的影响域足够大,而它本身的逻辑深度又足够小,它被移除后它的影响域都会成为逻辑深度足够大的节点的子节点,那么这个节点的影响力就有可能是负数——这便是在之前的章节中所提到的内容。
上述这种美好的性质我们当然希望可以一直延续到对等价网中等价类节点的价值的计算中,从而可以简单地获得关于这张网中每个等价类的影响力的信息。
但简单的分析却发现这样的计算是很难完成的。
在压缩林中,这样的计算之所以有效,是因为整个网络是分层的,而且压缩链就是逐渐从一层走到后一层,依次向逻辑深度越来越深的方向走。但在等价网中,虽然我们通过等价关系使得生成链具有从Root到Leaf且不自相交的性质,但却无法保证生成链中每个节点都比之前的节点的逻辑深度更深。
事实上,对于等价网中的生成链,我们大约只能保证这么几点:
- 每根生成链的起点都是Root节点,终点都是Leaf节点;
- 生成链中除了起点与终点,别的位置不可能是Root或Leaf节点;
- 每根生成链都不自相交,即生成链中的元素不会出现第二次;
- 生成链中第n个节点的逻辑深度不大于n。
因此,在等价网中,一个等高面i的节点可以生成比等高面i更低的节点,也可以生成比等高面i更高的节点,或者等高面i内的节点。这样导致的一个问题,就是我们在压缩林中所采用的求和方法在这里几乎肯定无法使用——一旦我们对等高面i求和,那么就会发现其中所涉及到的对子代的求和部分将无法自然地表达为某个确定的等高面的求和,从而压缩林中的求和方案无效。
归根到底,压缩林除了是一张全序图,同时还是可分层的,但等价网虽然是全序的,却不是可分层的。
对于一张可分层的等价网——即等高面i中的节点所生成的所有子元素都是等高面i+1的节点,那么我们才有可能将压缩林中的计算方案用到这里,而此时计算的结果也将变得非常Trivial,和压缩林中的总价值具有相同的形式——这也就是说,在不改变每一层节点数的情况下,无论如何修改等价网中节点之间的连线结构,都不会改变整张网的总价值。
但,可分层等价网只是等价网中一个极罕见的特例,在更多的情况下我们并不能简单地获得如上结论,所以关于节点价值以及图总价值的计算就陷入了困境。
比如,让我们来看一个例子:
这是一张可分层全序图,节点旁所标注的分别是节点的价值与影响力,左侧是Root,右侧是Leaf,连线都是从Root端指向Leaf端。同时我们可以很容易地看出图中只有三个节点拥有非空的专属子域,分别是第二层最下方的点、第三层中间的点以及第四层最上面的点,其中第二层的那个节点拥有三个专属子节点,其重要性可见一斑。
这里的两张图是在第一张图的基础上做了一定的修改。
上面的一张是添加了从L 2指向L 3的一根连线,但图依然是可分层全序图,所以对每一层等高面的总价值都不发生改变,自然也就不会改变全图总价值了。在L 3以上的等高面上的节点的价值与影响力都保持不变,而只有在该层及以下的等高面上,价值与影响力才会发生同一层内的再分布调整。
而下面那张图则是添加了L 3内的一根层内连线,从而使得整张图不再是可分层全序图,虽然依然是全序图。由于这条连线的出现,全图的总价值升高,每一层的总价值也发生了变化,且在前面一种形变下不发生改变的L 4与L 5的节点的影响力现在也发生了调整。
这张图中,是增加了L 3中点与L 4上点之间的连线,只不过这两张图中连线的方向相反,从而左侧的图不再是可分层全序图,右侧的图依然是可分层全序图。
可以看到,左侧的图中发生的变化比较大,尤其是L 2下点的影响力发生了巨大的下降,这是因为本来L 3中点是只有它可以生成的,但现在这个唯一性被破坏。这条连线也使得L 4上点的价值与影响力大幅提升。
由此可见,不可分层的全序网,也就是最一般的等价网,有着很不一般的特性哦。
上面的计算部分仅仅是一个简单的助兴,下面开始考虑一些更加复杂,但却更加有用的结构。
在我们最开始的讨论中,图灵覆盖的一个限制条件就是:它的所有图灵机都是将一个字符串输入而输出一个字符串的,从而是一个单进单出的结构。
现在让我们对这个条件进行拓展——允许图灵覆盖中的图灵机是多进单出的结构,即使多个字符串可以一同作为输入,而最终输出一个字符串。
在这个情况下,我们依然可以讨论不可压缩表示与最简生成,只不过此时不可压缩表示的衡量标准中的“最短字符串”改成了“最短字符串总长”。生成关系当然也可以被保留。
这种多对一的关系其实可以分解为两个步骤,第一步是将多个字符串“无脑”粘合为一个字符串,而第二步则是将这个新的字符串作为输入输入到之前定义的单进单出的图灵机中。
因此,现在我们只不过是允许“粘合机”出现在整个图中罢了。
它会带来什么样的结果呢?
可以看到,由于这种多对一关系的出现,即便考虑的是压缩链的情况,在此前压缩链只在朝着Leaf的方向分叉而在朝着Root的方向归一,但现在却在朝着Root的方向也会是分叉的。
因此,原本的压缩林,现在会变成一张压缩网,而且这张网很有可能不再是可分层的——因为既然是利用两个节点来生成下一个节点,那这两个节点就未必恰好位于同一个等高面上。
由于节点的父节点现在不唯一,所以从一个节点开始的寻找不可压缩表示的过程也将变得开始分叉起来。当然,虽然现在原本以不可压缩表示构筑起来的链式结构消失了,但不断寻找不可压缩表示的过程至少还是肯定有终点的,虽然这种特性现在看来已经变得有点过于微弱了。
压缩林到压缩网的改变使得很多原本压缩林具有的基于父节点的唯一性而来的美好形式都失去了,而这对于等价网来说自然就带来了更多的变化。
由于多对一连接的出现,在考虑节点的父代的时候,这种Link将只作为一根连线来考虑,而在考虑子代的时候,则不再作为一根连线,而是要考虑上一个配分权重。
因此,多对一的连接除了改变节点之间的连接关系,还将有一个重要的性质,那就是作为输入的多个节点之间的配分权重,权重在每个节点上都是0到1之间的常值,而其总和为1。在对节点的价值的计算过程中的对子节点价值的求和,也会发生变化:
可见,当Num(s)为1的时候就从等价类回到了生成云;当从s指向a的连接的权重因子Weight(s,a)为1的时候,这个连接自然就是一对一的连接,从而问题就回到了等价网的时候;当p a为1的时候,问题就回到了压缩网,如果进一步要求Weight为1,那就回到了压缩林。
从另一个角度来说,我们事实上也可以将现在多对一的连接给看做依然是一根根一对一的连接,只不过现在所有的连接都被赋予了一个0到1之间的权重因子,且被分成了若干组,每一组一对一的连接都拥有一个共同的终点,而同一组的连接的权重因子的总和为1。
所以说,显而易见,等价网才是讨论这类问题的最终工具啊。
前面啰里吧嗦说了这么多数学结构方面的内容,其实都只是铺垫——对,长达一万三千字的铺垫。
其核心内容,无非两部分:
- 给定字符串集S与图灵机集合T,并且T中图灵机可以赋予S中的字符串“生成”的关系,从而构成一张复杂的相互关联的网络;
- 利用有向图这一工具,在给定等价关系后构造出等价网,并计算这张网中不同节点的价值与影响力。
而这么做的目的,却是非常显而易见的:找出S中哪些字符串比别的字符串更重要,以及哪些图灵机比别的图灵机更重要。
单个字符串或者单个图灵机本身的属性,我们都是比较熟悉的。
比如对于字符串来说,最重要的几个属性当然就是字符串的长度,以及K氏复杂度与逻辑深度(忘了的朋友可以看这篇文章);而图灵机的几个重要的属性则包括长度、可接受字符串、执行深度以及K氏复杂度和逻辑深度(在给定通用图灵机后,任意图灵机其实都是以字符串的形式存在的)。
但这些性质都是将字符串与图灵机从整个所处的环境中剥离后单独看来的。当一个字符串或者一台图灵机融入到一个体系中以后,它的作用就完全不同了。
而分析在这样的一个环境中一个字符串与一台图灵机的作用,就比较有趣了。
而且,在实际情况中,由于图灵机本身也是字符串,因此实际情况下在上述体系中,一个生成云中的节点本身还可能对应了一大类节点之间的连线,从而这个情况就会变得非常复杂。
事实上,如果我们考虑现在这个网络上的一个动态生长过程——在复杂网络的研究中这是一个非常普遍的课题,即在给定一组生长规则后,来看整个网络随着时间会如何演变,尤其是度分布的变化。当然了生长也未必都是“长”,也可以有破坏的过程,比如随机破坏等,从而在这类动态过程中我们也会研究网络的断裂等等问题。
当我们考虑字符集的一个动态增加的过程时,我们自然也就在考虑图灵覆盖的动态增加过程,从而此时每个节点的重要性就有了更进一步的涵义——一个节点,包括Leaf,在新增一个Leaf后对整个网络能带来什么样的总价值变化呢?因此,这或许可以帮助我们来决定这么一个动态规划领域的问题:到底哪些字符串或图灵机是更值得去研究它们可以生成哪些新节点的。
因此,在给出了等价网(依赖于生成云与等价关系)后,我们依然有很多内容可以研究。
事实上,这样的工具与视角本身却并不只局限在字符串与图灵机这一组关系中——这里吐槽我自己一下,一万三千字的铺垫之后说字符串和图灵机的怎么这么少啊喂这到底是怎么回事!!!
我们都知道,图灵机和形式理论之间的关系是非常密切的,因此上面的这组关系事实上也可以被移植到形式理论这个大系统中。
理论可以认为是有公理与命题通过逻辑构筑出来的一座大厦。
公理,是理论的基石,而且一般而言几乎是无法被证明其正确还是错误的,只能选择相信它们是正确的。
比如说,没人会说几何学的第五公设到底是正确的还是错误的,你能做的只是去选择接受它或者不接受它——接受第五公设,我们可以得到平直的欧几里得几何学,而如果选择不接受第五公设,那么你可以得到弯曲的黎曼几何学。
在自然科学领域,人们总可以通过实验这一手段在一定程度上帮助人们决定到底是相信还是不相信某些基本假设,但很多时候并不能做到100%判定某个基础假设是正确的还是错误的——比如最近十多年大热的超对称,在LHC的实验数据下,虽然人们悲观,但却不能说超对称肯定就是错的。同样的,关于时空到底是平直的还是弯曲的(从而大致来说对应了力纲领与几何纲领),虽然我们都知道现在实验基本上都是支持弯曲时空的,但理论上来说我们依然可以构造出基于平直时空观的物理理论并且能在实验上做到和实验数据吻合——只不过这样的理论的数学表达往往是非常丑陋的。
而,在非自然科学领域,由于没有实验这一重要的帮忙筛选的手段,我们就更加无法判断一个基础假设到底是对的还是错的了——世界到底是绝对唯物的还是我们都是某位红心国王做的一场梦里的虚幻角色?这没人能说清。
在这个层面上,基础假设无法被证明或者证伪,你能做的只是去相信罢了。
而,公理可以通过逻辑推理推导出命题,命题也可以通过逻辑推理推导出别的命题,因此公理与命题构成的整个集合之间,可以通过逻辑推理构造出一系列的有向箭头,从而构成一张有向图。
为何是有向箭头?因为一个命题可以推导出另一个命题,不表示反过来的推导关系也成立,比如下面这两个命题:
命题1:自然数的乘法等于连续加法,其中被加数与加数都为被乘数而连加次数为乘数。
命题2:如果两个数字之和为3、之积为2,那么这两个数字一个是1一个是2。
很显然,第一条可以推导出第二条,而第二条却无论如何无法推导出第一条。
因此,将所有的公理与命题作为一个离散集合,而将逻辑作为图灵覆盖,命题长度作为判断不可压缩的标准,那么我们就可以很自然地得到之前所给出的那些东西:压缩林、生成云、等价网。
进而,我们现在可以得到一个选定的公理、命题集中每个命题的价值、影响力、不可替代价值与不可替代影响力,从而来判断哪些命题、公理是真正重要的东西。
即便引入两个命题一起来获得别的命题这种经典逻辑的三段论的形式,我们依然可以利用等价网来做分析,只不过现在需要在整个图上引入多对一连接,而这也就是我们之前在数学模型中最后所分析的那类情况。
而且,和字符集-图灵机这个体系中的情况不同,现在一些命题、公设可以更显然地呈现出负影响力,因为命题就和图灵机一样,现在既是节点也是连线,而命题和图灵机不同的是,它不但可以生成,也可以破坏。
比如由于第五公设的存在,许多非平直几何中的结论会变得Trivial甚至消失,从而在存在第五公设这个节点的情况下,很多原本可能存在的不同节点之间的连线现在反而消失了,因此第五公设的影响力便是一个显而易见的负值。
在物理领域也存在这样的负值节点,比如牛顿的绝对时空观,以太,甚至于,能量守恒与主能量条件。
我们可以想到,如果宇宙不要求能量守恒,或者宇宙没有主能量条件,那该会出现多么绚烂多姿的内容啊!
PS:由于主能量条件的存在,宇宙时空将几乎铁定不可能有时间机器,也不可能有让人瞬间移动的虫洞,折叠引擎也几乎没可能。
从整个理论体系的发展来看,那些负影响力的节点如何调整,大概可以算作是提高整个理论价值的重要环节。
另一方面,有很多时候某些被当做Root节点而存在的假设,却可能在某些领域的研究获得突破后,被发现其实是那些领域的Leaf节点的理论的衍生品,那么这样的研究自然会将整个理论体系的价值提升不少——在此前压缩林的分析中我们就发现,越是靠近Leaf的节点的价值越高,在等价网的情况下虽然由于可分层性的却是而没有如此明确的结论,但大致趋势还是类似的。
这样的情况在唯象理论的形式化与体系化的过程中是非常常见的,原本一些唯象理论只能建立在某些知其然不知其所以然的假设上,在形式化体系化后却可能发现这些假设实际上是某些更基本理论的自然导出。
在理论体系中,我们除了可以通过这样的工具来分析每个理论、每条命题的价值与影响力(无论是否是不可替代的)更重要的是我们也许可以通过这样的工具来分析不同理论(在现在的图景下一个理论就是一个点集)之间的相互关系。
比如,两个不同理论之间的节点是否存在等价关系?如果存在的话,那么这两个理论显然在很多方面是非常相似的。比如纯理论数学与理论物理最前沿的某些领域恐怕就会存在这样的相似性,比如范畴与代数几何。
而后,是否一个理论完全可以由另一个理论导出?比如物理与化学的关系。
或者,分析不同理论的Root节点的数量也是非常有意思的,比如不同数学领域的最基础假设有哪些?物理理论呢?特别是在物理领域往往针对同一个现象我们有大量不同的理论,比如当下绵延数年的String与Loop的争论,那么我们自然可以分析者两个理论的生成云的结构,尤其是它们都必须在低能近似下回归到我们已有的理论,从而就是说这两类点集在Leaf端都会连接到同一组节点上,那么由这组节点的价值来推算这两个点集本身的价值与影响力,大概会很有意思吧。
甚至于,我们还可以考虑如果更换一套“逻辑”,整个理论会如何——我们都知道,在形式理论系统中,人们都使用一套沿用数百年的逻辑,但,如果换一套逻辑推理方法呢?比如说,我们抛弃排中律,引入类似模糊逻辑的非确定性逻辑体系,除了绝对的对与绝对的错,还有一个对错百分比甚至不可判定对错,那么各不同命题之间的关系恐怕就会发生大变样了。
或者,我们放弃形式逻辑,使用非形式逻辑来作为理论构建的基础(这一混搭好奇葩啊……有一种出租车司机大叔的即视感……),会如何呢?
除此之外,这种生成与推导的关系,除了在字符串-图灵机系统以及理论系统中可以用之外,还可以继续外推。
将各种不同的理论与技术作为节点,我们当然也可以分析它们之间的有向网络结构的性质。
甚至于,我们也可以将“资源”与“产品”纳入考虑,从而现在就有了资源、理论、技术与产品这四大类的节点。
很显然,理论产生技术,技术也产生技术,技术还可以与资源结合生成产品,并和产品结合生成新的产品,所以资源与产品是纯节点,而理论与技术则既是节点又是有向箭头。
当然,在这种情况下,原本在价值定义中除了继承部分之外的那个常数1(在等价网中就是节点等价类s的元素个数Num(s)),就可以用一些更能反映节点所对应的资源或者技术或者产品的值来代替。
这样的系统构筑成一张宏大的网,可以将人类社会的大部分活动都包括进去,比如下面这一简单的案例——
让我们来考虑卡坦岛(囧囧囧囧囧)。
卡坦岛的所有节点可以显而易见地分为三层。
第一层是出产资源的格点,当然主要是格点的数字——从2到12,除了7(我们这里不考虑海盗与强盗)。
第二层是每个数字出产的资源:羊毛、小麦、木材、砖头、铁矿石。
第三层则是这些资源所能生产的建筑:道路、村落、堡垒(不考虑技能卡)。
显然,第一层是Root,第一层的节点与第二层的节点之间是多对多的关系,第二层节点到第三层节点也是多对多的关系,而第三层之间还有生成关系,真正的Leaf只有一个,那就是堡垒。
比如这么一个极端的情况:数字2和3只生产羊毛,数字4和5只生产小麦,数字6和8只生产木材,数字9和10只生产砖头,数字11和12只生产铁矿石。这是有卡坦岛的地图布局随机决定的,这里不纠结细节。
而后资源与建筑的关系是游戏规则决定的:木材与砖头生成道路,每个的权重都是0.5;羊毛、小麦、木材、砖头、道路生成村落,四个资源的权重为六分之一,而道路的权重为三分之一;小麦、铁矿石、村落生成城堡,小麦的权重为三分之一,铁矿石的权重为二分之一,村落的权重为六分之一。
此外,城堡本身分值为2,而村落的分值为1,别的节点的分值都为0,这也是游戏规则所确定的。
而整个网络本身其实也是动态的:一开始大家只能造村落,而后随着村落的出现就可以造城堡,所以可以分为两个阶段。
于是,整个网络在这两个阶段中每个节点的价值为(这里继承因子选为1):
前期
| Item | Value |
|---|---|
| 数字 | |
| 2,3 | 1/12 |
| 4,5 | 1/12 |
| 6,8 | 1/6 |
| 9,10 | 1/6 |
| 11,12 | 0 |
| 资源 | |
| 羊毛 | 1/6 |
| 小麦 | 1/6 |
| 木材 | 1/3 |
| 砖头 | 1/3 |
| 矿石 | 0 |
| 建筑 | |
| 道路 | 1/3 |
| 村落 | 1 |
后期
| Item | Value |
|---|---|
| 数字 | |
| 2,3 | 1/9 |
| 4,5 | 4/9 |
| 6,8 | 2/9 |
| 9,10 | 2/9 |
| 11,12 | 1/2 |
| 资源 | |
| 羊毛 | 2/9 |
| 小麦 | 8/9 |
| 木材 | 4/9 |
| 砖头 | 4/9 |
| 矿石 | 1 |
| 建筑 | |
| 道路 | 4/9 |
| 村落 | 4/3 |
| 城堡 | 2 |
这么一来,什么样的资源最重要,什么样的数字最重要(当然,在实际游戏中还要考虑不同数字出现的概率),就比较直观了。
当然,这里忽略了游戏中的一些额外因素,比如几个奖励方案,交易,技能卡,等等。
是不是很有意思?
当然,在此前的分析中,有一些情况还是值得商榷的。
比如,我们可以为每个节点s赋予一个特定的“固有价值”Vs,取代原本固定的1。
在选1作为固有价值的时候,这是基于该节点可以生成一条字符串或者一条定理/命题而言的,但对于更加具体的情况中,我们却可以认为这个值并不是固定为1。
因此,在这种情况下,等价网中节点(为等价类)c的价值就可以由下式给出:
这样,在卡坦岛例子中城堡的价值2与村落的价值1以及别的节点的价值0就有了合理的源头——整套游戏的规则。
与此同时,当我们认为每个节点可以具有非1的固有价值的同时,我们也可以考虑另一个问题:当有多个Root的时候,每个Root可能会有截然不同的权重,那么此时整张等价网中节点的影响力又要如何计算呢?
为此,我们引入节点s上的“ 流量”Flow(s):
其中Root节点的Flow(r)则是通过其余的边界条件来给定,比如在字符串-图灵机体系中可以认为就是Root节点数的倒数。
对于压缩林,显然这是一个常量,而且在单株压缩树的情况下可以认为这个常值就是1。
从而,我们可以利用节点上的价值与流量定义节点的“ 局部影响力”:
进一步,节点的影响力则可以通过比对移除节点前后图的总局部影响力来获得。
对于压缩林的情况,显然这样给出的影响力的定义与之前是等价的,但对于更加复杂的等价网,则会给出更多更丰富的内容。
因此,最终判断一个节点影响力的,应该就是基于局部影响力的节点的不可替代影响力Us了吧。
本质上来说,这套工具所处理的对象,基本都满足如下特性:
- 节点之间存在生产与被生产的关系;
- 有些节点本身决定了上述生产与被生产的关系;
- 越是上层的节点,单点价值可能更重要,但实际影响力却未必;
- 越是底层的节点,不可替代的影响力往往也越大。
同时,就和字符串-图灵机这个体系中每个节点都有长度、逻辑深度与K氏复杂度这些属性一样,如果我们为这套系统所能处理的问题中的每个节点都引入一套评价方式,比如某种本征属性值——以字符串的长度为例——那么,一个很有趣的问题就出现了,那就是随着节点越来越远离Root,这一本征属性是如何改变的?
在字符串-图灵机系统中,我们基本可以认为,深度值越大的节点的长度也越大,因此随着压缩链从Leaf往Root走,这基本可以看做是一个在有效信息量不变的限制下字符串的压缩程度越来越高的这么一个过程。而且,越是“浓缩”的信息可能越是只能成为更少的图灵机可接受的内容。因此,压缩的过程事实上也是一个不断剥夺被多重解释的可能性的过程,即一个子节点数越来越少的过程。
同样的过程也发生在理论体系中。在这里推导链越是靠近Root端,节点对应的理论/命题就越基本。而越是基本的命题/定理,其能直接衍生出的子命题/定理恐怕也就越少,必须随着命题/定理的越来越多,“逻辑深度”越来越大,才能更多地引发出新的命题/定理来。
在资源的问题中也是如此。Root节点对应的可以看做是未开采的那些矿石,比如贵重金属、稀有金属、石油与煤炭,而随着逻辑深度的提高,这些基础资源不断派生出更多种类的资源,比如从石油中我们可以提炼出柴油、汽油、塑料、人造纤维,等等等等,这些逻辑深度更大,从而更“次一级”的资源,才能具有比直接给你一滩石油更大的发展可能,可以衍生出更多的新产品,新资源。
这样的现象可以被归类为“创造力指数定律”,或者更应该说是一种猜想。
与开始的纯粹的数学工具不同,在那套工具中,这样的现象是非必须的。但在实际情况中,却是存在这这样的可能性。
从另一个角度来说,由于上述系统的一大特征就是节点本身同时也代表了连线,从而随着节点的增多,可用的连线也就更多,那么子节点数当然会增加,这本身就是一种必然的现象。
但这种现象是随着动态过程中新增加的子节点的分布而来的,是时域上的指数型,却也并不是创造力指数定律所要求的空域上的指数型。
因此,越是远离Root区的节点就具有更高的被开发利用并进而衍生出新节点的可能性,这样的结果本身大概可以看做是资源-技术、命题-定理、字符串-图灵机这些系统的一个根本属性吧。
嗯,这次的脑洞基本上就开到这里,打完收工!
本文遵守创作共享CC BY-NC-SA 4.0协议
通过本协议,您可以分享并修改本文内容,只要你遵守以下授权条款规定:姓名标示 、非商业性、相同方式分享。
具体内容请查阅上述协议声明。
本文禁止一切纸媒,即印刷于纸张之上的一切组织,包括但不限于转载、摘编的任何应用和衍生。网络平台如需转载必须与本人联系确认。
如果喜欢,想要下载App的话,轻戳这里~~
私人推荐订阅专题:《有意思的文章》、《严肃码匠圈》