【编程能力不行？那就写啊！】二叉索引树

正文

今天看算法竞赛入门指南，看到了一个叫做《区间信息的维护与查询》的章节，然后在本章节的第一小点介绍了一种二叉索引树的概念，当初自学数据结构的时候学过，现在再来看。握草？？！！！完全不知道在说啥。什么是lowbit？？辅助数组要干嘛？？瞎鸡儿搞~ 本来想直接跳过，后来想想还是好好学一把吧！结果就懂了~

算了，自己看看就好，就不丢人现眼了

正文

本文直接借鉴下面的博客进行补充：
区间信息的维护与查询（一）——二叉索引树（Fenwick树、树状数组）

我们有一个动态连续和查询问题：给定一个n个元素的数组A[1]、A[2]、A[3]、……A[n]，你的任务是设计一个数据结构，使得其支持以下两个操作：

• 1：Add（x，d）操作：让A[x]增加d；

• 2：Query（L,R）操作：计算A[L]+A[L+1]+……+A[R]。

第一种思路就是循环累加，这样每次的时间复杂度都是O（n）级别的。这样在数据很大的情况之下，是一定会效率很低的，所以我们引进了二叉索引树（也就是树状数组）这种比较高级的数据结构，说它高级，也高不到那里去，也就是比原先我们学过的数据结构难一些就是了。好吧，对我来说初步看的时候挺难得，自己写几下就好多了。

在讲BIT之前，我们来先了解一个函数：对于任意正整数x，我们定义lowbit（x）为x的二进制中最右边的1所对应的值，比如，5的二进制是101，那么lowbit（5）= 1；4的二进制是100，那么lowbit（4） = 4；在程序实现中，lowbit代码如下

lowbit（x） = x&(-x)

这里用到的是按位运算。计算机里面的整数采用补码表示，-x实际上是x在二进制中按位取反，末位+1后的结果，二者按位取“与”之后，前面全部变成0，之后的lowbit保持不变；

38288= 10010101100{10000}
-38288=01101010011{10000}
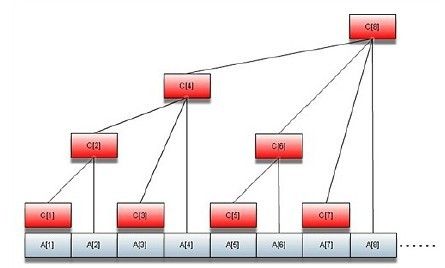
从这儿你可以自己算算，38288整个取反之后是01101010011{01111}，再+1 就是01101010011{10000}，所以这样来说是不是容易懂些呢？接下来给大家附上一张BIT 的图，其实也不是很难懂，但是我想要的图我找不到了，所以就附一个别的图吧，希望大家能尽量去看，在下面我会给大家解释其中C数组的含义（这是原博客中附带的图，我下面贴张我从书上看到的图，我觉得更好的理解）

image

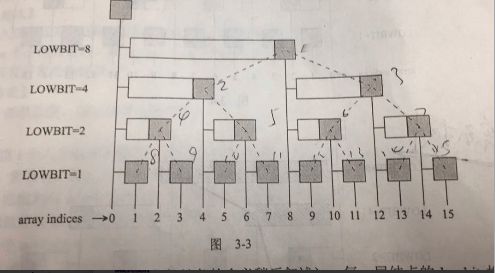
我的书上的图，别看我瞎写的那些，这个的那些黑坨坨就是C[i]下面有一个下标索引的，看见没？array indices那个。这个是在原来的数组A[i]上进行的整合，

image.png

其中我们可以看到C[i]是有分层问题的，那么到底是怎么分层的呢，实际上就是根据lowbit（i）的值来分的层。

在这里我们可以看到BIT是有连线的，但实际上这些连线在计算机中并不存在，只是为了读者好理解才加上的。其实BIT本身就是一棵二叉树（具体请翻阅前面BIT的定义），那么这棵树上面就会有父亲节点和左右儿子节点（实际上在图中没有看到右孩子与父亲节点的连线，我们可以想象一下）关于在BIT上节点的父子关系，我们是这样定义的：

对于节点i，如果它是左子节点，那么它的父节点的编号为i+lowbit(i)；如果它是右子节点，那么它的父节点编号为i+lowbit(i)。大家可以自己证明一下这个东西。搞清楚BIT 结构之后，我们来讲一下这个 C[] 数组是干嘛的。

C数组实际上只是个辅助数组，其中C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+……+A[i];可以看出，C数组就是用来辅助计算前缀和S[i]的；

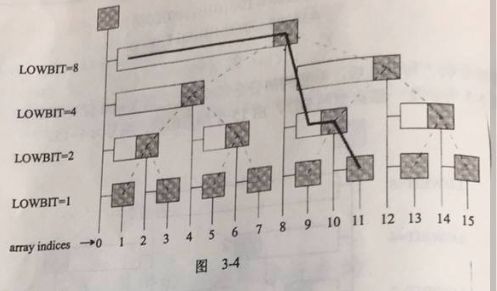
那么我们有了C数组之后，如何计算S[i]呢？顺着i节点往左走，边走边往上爬（这里请注意，不一定沿着BIT中的边爬），把沿途的C[i]累加起来就好了（请读者注意，这里沿途经过的C[i]毫无遗漏和重复的走完了A[i]），那么下面我给大家附上这个求前缀和操作的代码（这里我只会给出核心代码，因为全部代码给出真的就是没必要）：

image.png

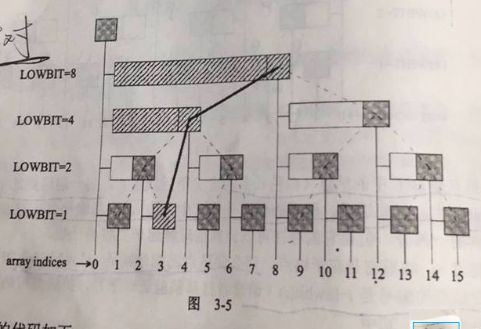
下面来讲一下修改问题，因为BIT是一棵树，而且根据前面的C[i]的定义，我们可以知道，当某个A[i]改变时，有一些C[i]也会改变，那么需要更改那些C数组中的元素呢？从C[i]开始往右走，边走边“往上爬”（同上，不一定要沿着图中的边爬），沿途修改经过所有节点对应的C[i]值即可。

image.png

这两个操作的时间复杂度都是O（logn）预处理方法是将A和C数组清空，再执行n次add操作，总时间复杂度为O（nlogn）；

整体代码如下：

#include
using namespace std;


int A[16]={100,1,2,3,4,5,6,7,8,9,10,11,12,13,14};
int C[16];
// 位运算，lowbit
int lowbit(int x)
{
    return x&(-x);
}
//求出在某个数之前的sum值，如果要求区间i,j这种的话，直接sum[j]-sum[i]即可
int sum(int x)
{
    int ret=0;
    while(x>0)
    {
        ret+=C[x];
        x-=lowbit(x);
    }
    return ret;
}

//在A[]数组中加某个数，会对组成的C[]数组的二叉索引树结构进行重构，对加了相应位置的C[]重新赋值
void add(int x,int d)
{
    while(x<16)
    {
        C[x]+=d;
        x+=lowbit(x);
    }
}


int main()
{
//初始化过程，A[]数组是一开始给定的要处理的数组，C[]数组是要构建二叉树的数组，利用lowbit可以在C[]各个位置之间进行跳跃，实现转移效果
    for (int i = 1; i < 16; ++i)
    {
        add(i,A[i]);
    }
    cout<<"* | ";
    for(int i=0;i<16;++i)
        cout<

下面是几个运行结果的展示：

image.png

int main()
{
    for (int i = 1; i < 16; ++i)
    {
        add(i,A[i]);
    }
    cout<<"* | ";
    for(int i=0;i<16;++i)
        cout<

image.png

正文之后

溜了溜了。不知诸位能否明白我这种理解了一个数据结构之后的喜悦？

image.png