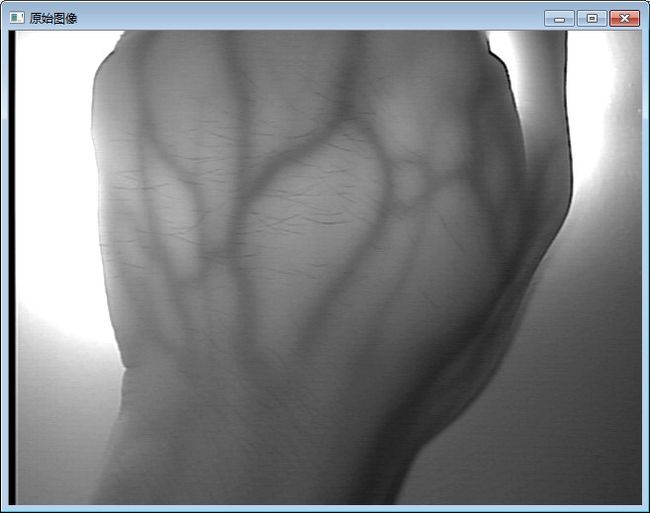
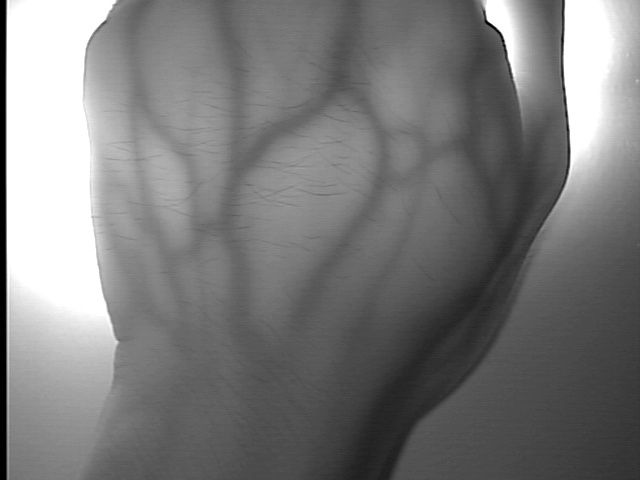
CLAHE算法对于医学图像,特别是医学红外图像的增强效果非常明显。
CLAHE https://en.wikipedia.org/wiki/Adaptive_histogram_equalization
中文方面非常好的资料 限制对比度自适应直方图均衡化算法原理、实现及效果
在OpenCV中已经实现了CLAHE,但是它在使用过程中,存在参数选择的问题。为了从根本上搞明白,我参考了网络上的一些代码
主要是来源 http://blog.csdn.net/abcd1992719g/article/details/25483395
实现了基于OpenCV的CLAHE实现和研究。从最基本的开始做,分别实现HE算法,AHE算法,CLHE算法和CLAHE算法。素材分别采用了手部和手臂的红外图片,同时调用OpenCV生成代码和自己编写代码进行比对。
调用代码和实现效果:
int _tmain(
int argc, _TCHAR
* argv[])
{
//读入灰度的手部图像
Mat src = imread( "arm.jpg", 0);
Mat dst = src.clone();
Mat HT_OpenCV;
Mat HT_GO;
Mat AHE_GO;
Mat CLHE_GO;
Mat CLAHE_Without_Interpolation;
Mat CLAHE_OpenCV;
Mat CLAHE_GO;
Mat matInter;
////OpenCV HT 方法
cv : :equalizeHist(src,HT_OpenCV);
////GO HT方法
HT_GO = eaualizeHist_GO(src);
////GO AHE方法
AHE_GO = aheGO(src);
////GO CLHE方法
CLHE_GO = clheGO(src);
////clahe不计算差值
CLAHE_Without_Interpolation = claheGoWithoutInterpolation(src);
////OpenCV CLAHE 方法
Ptr <cv : :CLAHE > clahe = createCLAHE(); //默认参数
clahe - >apply(src, CLAHE_OpenCV);
////GO CLAHE方法
CLAHE_GO = claheGO(src);
////结果显示
imshow( "原始图像",src);
imshow( "OpencvHT",HT_OpenCV);
imshow( "GOHT",HT_GO);
imshow( "GOAHE",AHE_GO);
imshow( "GOCLHE",CLHE_GO);
imshow( "GOCLAHE",CLAHE_GO);
imshow( "CLAHE_Without_Interpolation",CLAHE_Without_Interpolation);
imshow( "OpencvCLAHE",CLAHE_OpenCV);
waitKey();
return 0;
}
{
//读入灰度的手部图像
Mat src = imread( "arm.jpg", 0);
Mat dst = src.clone();
Mat HT_OpenCV;
Mat HT_GO;
Mat AHE_GO;
Mat CLHE_GO;
Mat CLAHE_Without_Interpolation;
Mat CLAHE_OpenCV;
Mat CLAHE_GO;
Mat matInter;
////OpenCV HT 方法
cv : :equalizeHist(src,HT_OpenCV);
////GO HT方法
HT_GO = eaualizeHist_GO(src);
////GO AHE方法
AHE_GO = aheGO(src);
////GO CLHE方法
CLHE_GO = clheGO(src);
////clahe不计算差值
CLAHE_Without_Interpolation = claheGoWithoutInterpolation(src);
////OpenCV CLAHE 方法
Ptr <cv : :CLAHE > clahe = createCLAHE(); //默认参数
clahe - >apply(src, CLAHE_OpenCV);
////GO CLAHE方法
CLAHE_GO = claheGO(src);
////结果显示
imshow( "原始图像",src);
imshow( "OpencvHT",HT_OpenCV);
imshow( "GOHT",HT_GO);
imshow( "GOAHE",AHE_GO);
imshow( "GOCLHE",CLHE_GO);
imshow( "GOCLAHE",CLAHE_GO);
imshow( "CLAHE_Without_Interpolation",CLAHE_Without_Interpolation);
imshow( "OpencvCLAHE",CLAHE_OpenCV);
waitKey();
return 0;
}
原始图像
GOCLAHE效果
OpenCV CLAHE效果
HE算法:
Mat eaualizeHist_GO(Mat src)
{
int width = src.cols;
int height = src.rows;
Mat HT_GO = src.clone();
int tmp[ 256] ={ 0};
float C[ 256] = { 0. 0};
int total = width *height;
for ( int i = 0 ;i <src.rows;i ++)
{
for ( int j = 0;j <src.cols;j ++)
{
int index = src.at <uchar >(i,j);
tmp[index] ++;
}
}
//计算累积函数
for( int i = 0;i < 256 ; i ++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i - 1] + 1.0f * tmp[i] / total;
}
//这里的累积函数分配的方法非常直观高效
for( int i = 0;i < src.rows;i ++){
for( int j = 0;j < src.cols;j ++){
int index = src.at <uchar >(i,j);
HT_GO.at <uchar >(i,j) = C[index] * 255 ;
}
}
return HT_GO;
}
int width = src.cols;
int height = src.rows;
Mat HT_GO = src.clone();
int tmp[ 256] ={ 0};
float C[ 256] = { 0. 0};
int total = width *height;
for ( int i = 0 ;i <src.rows;i ++)
{
for ( int j = 0;j <src.cols;j ++)
{
int index = src.at <uchar >(i,j);
tmp[index] ++;
}
}
//计算累积函数
for( int i = 0;i < 256 ; i ++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i - 1] + 1.0f * tmp[i] / total;
}
//这里的累积函数分配的方法非常直观高效
for( int i = 0;i < src.rows;i ++){
for( int j = 0;j < src.cols;j ++){
int index = src.at <uchar >(i,j);
HT_GO.at <uchar >(i,j) = C[index] * 255 ;
}
}
return HT_GO;
}
AHE算法:
Mat aheGO(Mat src,
int _step
=
8)
{
Mat AHE_GO = src.clone();
int block = _step;
int width = src.cols;
int height = src.rows;
int width_block = width /block; //每个小格子的长和宽
int height_block = height /block;
//存储各个直方图
int tmp2[ 8 * 8][ 256] ={ 0};
float C2[ 8 * 8][ 256] = { 0. 0};
//分块
int total = width_block * height_block;
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
tmp2[num][index] ++;
}
}
//计算累积分布直方图
for( int k = 0 ; k < 256 ; k ++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total;
}
}
}
//将统计结果写入
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
//结果直接写入AHE_GO中去
AHE_GO.at <uchar >(jj,ii) = C2[num][index] * 255 ;
}
}
}
}
return AHE_GO;
}
{
Mat AHE_GO = src.clone();
int block = _step;
int width = src.cols;
int height = src.rows;
int width_block = width /block; //每个小格子的长和宽
int height_block = height /block;
//存储各个直方图
int tmp2[ 8 * 8][ 256] ={ 0};
float C2[ 8 * 8][ 256] = { 0. 0};
//分块
int total = width_block * height_block;
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
tmp2[num][index] ++;
}
}
//计算累积分布直方图
for( int k = 0 ; k < 256 ; k ++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total;
}
}
}
//将统计结果写入
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
//结果直接写入AHE_GO中去
AHE_GO.at <uchar >(jj,ii) = C2[num][index] * 255 ;
}
}
}
}
return AHE_GO;
}
CLHE算法:
//这里是在全局直方图加入“限制对比度”方法
Mat clheGO(Mat src, int _step = 8)
{
int width = src.cols;
int height = src.rows;
Mat CLHE_GO = src.clone();
int tmp[ 256] ={ 0};
float C[ 256] = { 0. 0};
int total = width *height;
for ( int i = 0 ;i <src.rows;i ++)
{
for ( int j = 0;j <src.cols;j ++)
{
int index = src.at <uchar >(i,j);
tmp[index] ++;
}
}
/////////////////////////限制对比度计算部分,注意这个地方average的计算不一定科学
int average = width * height / 255 / 64;
int LIMIT = 4 * average;
int steal = 0;
for( int k = 0 ; k < 256 ; k ++)
{
if(tmp[k] > LIMIT){
steal += tmp[k] - LIMIT;
tmp[k] = LIMIT;
}
}
int bonus = steal / 256;
//hand out the steals averagely
for( int k = 0 ; k < 256 ; k ++)
{
tmp[k] += bonus;
}
///////////////////////////////////////////
//计算累积函数
for( int i = 0;i < 256 ; i ++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i - 1] + 1.0f * tmp[i] / total;
}
//这里的累积函数分配的方法非常直观高效
for( int i = 0;i < src.rows;i ++){
for( int j = 0;j < src.cols;j ++){
int index = src.at <uchar >(i,j);
CLHE_GO.at <uchar >(i,j) = C[index] * 255 ;
}
}
return CLHE_GO;
}
Mat clheGO(Mat src, int _step = 8)
{
int width = src.cols;
int height = src.rows;
Mat CLHE_GO = src.clone();
int tmp[ 256] ={ 0};
float C[ 256] = { 0. 0};
int total = width *height;
for ( int i = 0 ;i <src.rows;i ++)
{
for ( int j = 0;j <src.cols;j ++)
{
int index = src.at <uchar >(i,j);
tmp[index] ++;
}
}
/////////////////////////限制对比度计算部分,注意这个地方average的计算不一定科学
int average = width * height / 255 / 64;
int LIMIT = 4 * average;
int steal = 0;
for( int k = 0 ; k < 256 ; k ++)
{
if(tmp[k] > LIMIT){
steal += tmp[k] - LIMIT;
tmp[k] = LIMIT;
}
}
int bonus = steal / 256;
//hand out the steals averagely
for( int k = 0 ; k < 256 ; k ++)
{
tmp[k] += bonus;
}
///////////////////////////////////////////
//计算累积函数
for( int i = 0;i < 256 ; i ++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i - 1] + 1.0f * tmp[i] / total;
}
//这里的累积函数分配的方法非常直观高效
for( int i = 0;i < src.rows;i ++){
for( int j = 0;j < src.cols;j ++){
int index = src.at <uchar >(i,j);
CLHE_GO.at <uchar >(i,j) = C[index] * 255 ;
}
}
return CLHE_GO;
}
CLAHE不包括插值算法:
Mat claheGoWithoutInterpolation(Mat src,
int _step
=
8)
{
Mat CLAHE_GO = src.clone();
int block = _step; //pblock
int width = src.cols;
int height = src.rows;
int width_block = width /block; //每个小格子的长和宽
int height_block = height /block;
//存储各个直方图
int tmp2[ 8 * 8][ 256] ={ 0};
float C2[ 8 * 8][ 256] = { 0. 0};
//分块
int total = width_block * height_block;
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
tmp2[num][index] ++;
}
}
//裁剪和增加操作,也就是clahe中的cl部分
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
int LIMIT = 4 * average;
int steal = 0;
for( int k = 0 ; k < 256 ; k ++)
{
if(tmp2[num][k] > LIMIT){
steal += tmp2[num][k] - LIMIT;
tmp2[num][k] = LIMIT;
}
}
int bonus = steal / 256;
//hand out the steals averagely
for( int k = 0 ; k < 256 ; k ++)
{
tmp2[num][k] += bonus;
}
//计算累积分布直方图
for( int k = 0 ; k < 256 ; k ++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total;
}
}
}
//计算变换后的像素值
//将统计结果写入
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
//结果直接写入AHE_GO中去
CLAHE_GO.at <uchar >(jj,ii) = C2[num][index] * 255 ;
}
}
}
}
return CLAHE_GO;
}
{
Mat CLAHE_GO = src.clone();
int block = _step; //pblock
int width = src.cols;
int height = src.rows;
int width_block = width /block; //每个小格子的长和宽
int height_block = height /block;
//存储各个直方图
int tmp2[ 8 * 8][ 256] ={ 0};
float C2[ 8 * 8][ 256] = { 0. 0};
//分块
int total = width_block * height_block;
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
tmp2[num][index] ++;
}
}
//裁剪和增加操作,也就是clahe中的cl部分
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
int LIMIT = 4 * average;
int steal = 0;
for( int k = 0 ; k < 256 ; k ++)
{
if(tmp2[num][k] > LIMIT){
steal += tmp2[num][k] - LIMIT;
tmp2[num][k] = LIMIT;
}
}
int bonus = steal / 256;
//hand out the steals averagely
for( int k = 0 ; k < 256 ; k ++)
{
tmp2[num][k] += bonus;
}
//计算累积分布直方图
for( int k = 0 ; k < 256 ; k ++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total;
}
}
}
//计算变换后的像素值
//将统计结果写入
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
//结果直接写入AHE_GO中去
CLAHE_GO.at <uchar >(jj,ii) = C2[num][index] * 255 ;
}
}
}
}
return CLAHE_GO;
}
CLAHE算法:
Mat claheGO(Mat src,
int _step
=
8)
{
Mat CLAHE_GO = src.clone();
int block = _step; //pblock
int width = src.cols;
int height = src.rows;
int width_block = width /block; //每个小格子的长和宽
int height_block = height /block;
//存储各个直方图
int tmp2[ 8 * 8][ 256] ={ 0};
float C2[ 8 * 8][ 256] = { 0. 0};
//分块
int total = width_block * height_block;
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
tmp2[num][index] ++;
}
}
//裁剪和增加操作,也就是clahe中的cl部分
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
//关于参数如何选择,需要进行讨论。不同的结果进行讨论
//关于全局的时候,这里的这个cl如何算,需要进行讨论
int LIMIT = 40 * average;
int steal = 0;
for( int k = 0 ; k < 256 ; k ++)
{
if(tmp2[num][k] > LIMIT){
steal += tmp2[num][k] - LIMIT;
tmp2[num][k] = LIMIT;
}
}
int bonus = steal / 256;
//hand out the steals averagely
for( int k = 0 ; k < 256 ; k ++)
{
tmp2[num][k] += bonus;
}
//计算累积分布直方图
for( int k = 0 ; k < 256 ; k ++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total;
}
}
}
//计算变换后的像素值
//根据像素点的位置,选择不同的计算方法
for( int i = 0 ; i < width; i ++)
{
for( int j = 0 ; j < height; j ++)
{
//four coners
if(i < = width_block / 2 && j < = height_block / 2)
{
int num = 0;
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
} else if(i < = width_block / 2 && j > = ((block - 1) *height_block + height_block / 2)){
int num = block *(block - 1);
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
} else if(i > = ((block - 1) *width_block +width_block / 2) && j < = height_block / 2){
int num = block - 1;
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
} else if(i > = ((block - 1) *width_block +width_block / 2) && j > = ((block - 1) *height_block + height_block / 2)){
int num = block *block - 1;
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
}
//four edges except coners
else if( i < = width_block / 2 )
{
//线性插值
int num_i = 0;
int num_j = (j - height_block / 2) /height_block;
int num1 = num_j *block + num_i;
int num2 = num1 + block;
float p = (j - (num_j *height_block +height_block / 2)) /( 1.0f *height_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
} else if( i > = ((block - 1) *width_block +width_block / 2)){
//线性插值
int num_i = block - 1;
int num_j = (j - height_block / 2) /height_block;
int num1 = num_j *block + num_i;
int num2 = num1 + block;
float p = (j - (num_j *height_block +height_block / 2)) /( 1.0f *height_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
} else if( j < = height_block / 2 ){
//线性插值
int num_i = (i - width_block / 2) /width_block;
int num_j = 0;
int num1 = num_j *block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i *width_block +width_block / 2)) /( 1.0f *width_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
} else if( j > = ((block - 1) *height_block + height_block / 2) ){
//线性插值
int num_i = (i - width_block / 2) /width_block;
int num_j = block - 1;
int num1 = num_j *block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i *width_block +width_block / 2)) /( 1.0f *width_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
}
//双线性插值
else{
int num_i = (i - width_block / 2) /width_block;
int num_j = (j - height_block / 2) /height_block;
int num1 = num_j *block + num_i;
int num2 = num1 + 1;
int num3 = num1 + block;
int num4 = num2 + block;
float u = (i - (num_i *width_block +width_block / 2)) /( 1.0f *width_block);
float v = (j - (num_j *height_block +height_block / 2)) /( 1.0f *height_block);
CLAHE_GO.at <uchar >(j,i) = ( int)((u *v *C2[num4][CLAHE_GO.at <uchar >(j,i)] +
( 1 -v) *( 1 -u) *C2[num1][CLAHE_GO.at <uchar >(j,i)] +
u *( 1 -v) *C2[num2][CLAHE_GO.at <uchar >(j,i)] +
v *( 1 -u) *C2[num3][CLAHE_GO.at <uchar >(j,i)]) * 255);
}
//最后这步,类似高斯平滑
CLAHE_GO.at <uchar >(j,i) = CLAHE_GO.at <uchar >(j,i) + (CLAHE_GO.at <uchar >(j,i) << 8) + (CLAHE_GO.at <uchar >(j,i) << 16);
}
}
return CLAHE_GO;
}
{
Mat CLAHE_GO = src.clone();
int block = _step; //pblock
int width = src.cols;
int height = src.rows;
int width_block = width /block; //每个小格子的长和宽
int height_block = height /block;
//存储各个直方图
int tmp2[ 8 * 8][ 256] ={ 0};
float C2[ 8 * 8][ 256] = { 0. 0};
//分块
int total = width_block * height_block;
for ( int i = 0;i <block;i ++)
{
for ( int j = 0;j <block;j ++)
{
int start_x = i *width_block;
int end_x = start_x + width_block;
int start_y = j *height_block;
int end_y = start_y + height_block;
int num = i +block *j;
//遍历小块,计算直方图
for( int ii = start_x ; ii < end_x ; ii ++)
{
for( int jj = start_y ; jj < end_y ; jj ++)
{
int index =src.at <uchar >(jj,ii);
tmp2[num][index] ++;
}
}
//裁剪和增加操作,也就是clahe中的cl部分
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
//关于参数如何选择,需要进行讨论。不同的结果进行讨论
//关于全局的时候,这里的这个cl如何算,需要进行讨论
int LIMIT = 40 * average;
int steal = 0;
for( int k = 0 ; k < 256 ; k ++)
{
if(tmp2[num][k] > LIMIT){
steal += tmp2[num][k] - LIMIT;
tmp2[num][k] = LIMIT;
}
}
int bonus = steal / 256;
//hand out the steals averagely
for( int k = 0 ; k < 256 ; k ++)
{
tmp2[num][k] += bonus;
}
//计算累积分布直方图
for( int k = 0 ; k < 256 ; k ++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k - 1] + 1.0f * tmp2[num][k] / total;
}
}
}
//计算变换后的像素值
//根据像素点的位置,选择不同的计算方法
for( int i = 0 ; i < width; i ++)
{
for( int j = 0 ; j < height; j ++)
{
//four coners
if(i < = width_block / 2 && j < = height_block / 2)
{
int num = 0;
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
} else if(i < = width_block / 2 && j > = ((block - 1) *height_block + height_block / 2)){
int num = block *(block - 1);
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
} else if(i > = ((block - 1) *width_block +width_block / 2) && j < = height_block / 2){
int num = block - 1;
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
} else if(i > = ((block - 1) *width_block +width_block / 2) && j > = ((block - 1) *height_block + height_block / 2)){
int num = block *block - 1;
CLAHE_GO.at <uchar >(j,i) = ( int)(C2[num][CLAHE_GO.at <uchar >(j,i)] * 255);
}
//four edges except coners
else if( i < = width_block / 2 )
{
//线性插值
int num_i = 0;
int num_j = (j - height_block / 2) /height_block;
int num1 = num_j *block + num_i;
int num2 = num1 + block;
float p = (j - (num_j *height_block +height_block / 2)) /( 1.0f *height_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
} else if( i > = ((block - 1) *width_block +width_block / 2)){
//线性插值
int num_i = block - 1;
int num_j = (j - height_block / 2) /height_block;
int num1 = num_j *block + num_i;
int num2 = num1 + block;
float p = (j - (num_j *height_block +height_block / 2)) /( 1.0f *height_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
} else if( j < = height_block / 2 ){
//线性插值
int num_i = (i - width_block / 2) /width_block;
int num_j = 0;
int num1 = num_j *block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i *width_block +width_block / 2)) /( 1.0f *width_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
} else if( j > = ((block - 1) *height_block + height_block / 2) ){
//线性插值
int num_i = (i - width_block / 2) /width_block;
int num_j = block - 1;
int num1 = num_j *block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i *width_block +width_block / 2)) /( 1.0f *width_block);
float q = 1 -p;
CLAHE_GO.at <uchar >(j,i) = ( int)((q *C2[num1][CLAHE_GO.at <uchar >(j,i)] + p *C2[num2][CLAHE_GO.at <uchar >(j,i)]) * 255);
}
//双线性插值
else{
int num_i = (i - width_block / 2) /width_block;
int num_j = (j - height_block / 2) /height_block;
int num1 = num_j *block + num_i;
int num2 = num1 + 1;
int num3 = num1 + block;
int num4 = num2 + block;
float u = (i - (num_i *width_block +width_block / 2)) /( 1.0f *width_block);
float v = (j - (num_j *height_block +height_block / 2)) /( 1.0f *height_block);
CLAHE_GO.at <uchar >(j,i) = ( int)((u *v *C2[num4][CLAHE_GO.at <uchar >(j,i)] +
( 1 -v) *( 1 -u) *C2[num1][CLAHE_GO.at <uchar >(j,i)] +
u *( 1 -v) *C2[num2][CLAHE_GO.at <uchar >(j,i)] +
v *( 1 -u) *C2[num3][CLAHE_GO.at <uchar >(j,i)]) * 255);
}
//最后这步,类似高斯平滑
CLAHE_GO.at <uchar >(j,i) = CLAHE_GO.at <uchar >(j,i) + (CLAHE_GO.at <uchar >(j,i) << 8) + (CLAHE_GO.at <uchar >(j,i) << 16);
}
}
return CLAHE_GO;
}
从结果上来看,GOCLAHE方法和OpenCV提供的CLAHE方法是一样的。
再放一组图片
代码实现之后,留下两个问题:
集中在这段代码
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
//关于参数如何选择,需要进行讨论。不同的结果进行讨论
//关于全局的时候,这里的这个cl如何算,需要进行讨论
int LIMIT = 40 * average;
int steal = 0;
int average = width_block * height_block / 255;
//关于参数如何选择,需要进行讨论。不同的结果进行讨论
//关于全局的时候,这里的这个cl如何算,需要进行讨论
int LIMIT = 40 * average;
int steal = 0;
1、在进行CLAHE中CL的计算,也就是限制对比度的计算的时候,参数的选择缺乏依据。在原始的《GEMS》中提供的参数中,
fCliplimit = 4 , uiNrBins = 255.
但是在OpenCV的默认参数中,这里是40.就本例而言,如果从结果上反推,我看10比较好。这里参数的选择缺乏依据;
2、CLHE是可以用来进行全局直方图增强的,那么这个时候,这个
average 如何计算,肯定不是width * height/255,这样就太大了,算出来的LIMIT根本没有办法获得。
但是就实现血管增强的效果而言,这些结果是远远不够的。一般来说,对于CLAHE计算出来的结果,进行Frangi增强或者使用超分辨率增强?结果就是要把血管区域强化出来。
p.s:
arm.jpg 和 hand.jpg