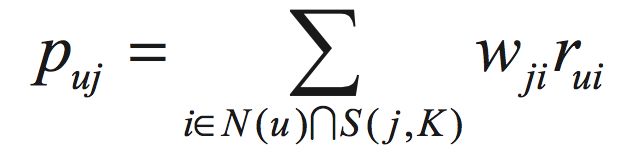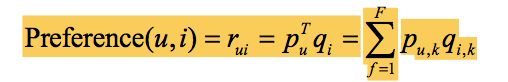1.用户行为数据
用户行为数据在网站上最简单的存在形式就是日志,比如用户在电子商务网站中的网页浏览、购买、点击、评分和评论等活动。
用户行为在个性化推荐系统中一般分两种——显性反馈行为(explicit feedback)和隐性反馈行为(implicit feedback)。显性反馈行为包括用户明确表示对物品喜好的行为。网站中收集显性反馈的主要方式就是评分和喜欢/不喜欢。隐性反馈行为指的是那些不能明确反应用户喜好的行为。最具代表性的隐性反馈行为就是页面浏览行为。
按照反馈的明确性分,用户行为数据可以分为显性反馈和隐性反馈,但按照反馈的方向分,又可以分为正反馈和负反馈。正反馈指用户的行为倾向于指用户喜欢该物品,而负反馈指用户的行为倾向于指用户不喜欢该物品。在显性反馈中,很容易区分一个用户行为是正反馈还是负反馈,而在隐性反馈行为中,就相对比较难以确定。
2.用户行为分析
在利用用户行为数据设计推荐算法之前,研究人员首先需要对用户行为数据进行分析,了解数据中蕴含的一般规律,这样才能对算法的设计起到指导作用。
2.1 用户活跃度和物品流行度
很多关于互联网数据的研究发现,互联网上的很多数据分布都满足一种称为Power Law的分布,这个分布在互联网领域也称长尾分布。
如果定义物品的流行度K为被K个用户产生过行为,而用户的活跃度K定义为对K个物品产生过行为,那么二者的分布大概如下图所示(横轴代表物品的流行度/用户的活跃度,纵轴代表物品数/用户数):
可以看到在双对数曲线上,不管是物品的流行度还是用户的活跃度,都近似于长尾分布(呈直线)。
2.2用户活跃度和物品流行度的关系
一般认为,新用户倾向于浏览热门的物品,因为他们对网站还不熟悉,只能点击首页的热门物品,而老用户会逐渐开始浏览冷门的物品。如果用横坐标表示用户活跃度,纵坐标表示具有某个活跃度的所有用户评过分的物品的平均流行度。图中曲线呈明显下降的趋势,这表明用户越活跃,越倾向于浏览冷门的物品。
仅仅基于用户行为数据设计的推荐算法一般称为协同过滤算法。学术界对协同过滤算法进行了深入研究,提出了很多方法,比如基于邻域的方法(neighborhood-based)、隐语义模型 (latent factor model)、基于图的随机游走算法(random walk on graph)等。在这些方法中,最著名的、在业界得到最广泛应用的算法是基于邻域的方法。
3.基于领域的算法
基于邻域的算法是推荐系统中最基本的算法,该算法不仅在学术界得到了深入研究,而且在业界得到了广泛应用。基于邻域的算法分为两大类,一类是基于用户的协同过滤算法,另一类是基于物品的协同过滤算法。现在我们所说的协同过滤,基本上就就是指基于用户或者是基于物品的协同过滤算法,因此,我们可以说基于邻域的算法即是我们常说的协同过滤算法。
3.1基于用户的协同过滤算法(UserCF)
基于用户的协同过滤算法的基本思想是:在一个在线个性化推荐系统中,当一个用户A需要个性化推荐时,可以先找到和他有相似兴趣的其他用户,然后把那些用户喜欢的、而用户A没有听说过的物品推荐给A。
从上面的描述中可以看到,基于用户的协同过滤算法主要包括两个步骤。
(1) 找到和目标用户兴趣相似的用户集合。
(2) 找到这个集合中的用户喜欢的,且目标用户没有听说过的物品推荐给目标用户。
这里,步骤1的关键是计算两个用户的兴趣相似度,协同过滤算法主要利用行为的相似度计算兴趣的相似度。给定用户u和用户v,令N(u)表示用户u曾经有过正反馈的物品集合,令N(v) 为用户v曾经有过正反馈的物品集合。那么我们可以通过以下两种方法计算用户的相似度:
基于jaccard公式
基于余弦相似度
余弦相似度为什么是上面这种写法呢,因为这里,我们并不是用的用户对物品的评分,而是用的0-1表示是否评了分,所以对两个集合做交集,相当于进行了点乘。如果我们的矩阵是用户对物品的评分,那么计算余弦相似度的时候可以利用用户的具体评分而不是0-1值。
如果简单的基于余弦相似度,显得过于粗糙,以图书为例,如果两个用户都曾经买过《新华字典》,这丝毫不能说明他们兴趣相似, 因为绝大多数中国人小时候都买过《新华字典》。但如果两个用户都买过《数据挖掘导论》,那可 以认为他们的兴趣比较相似,因为只有研究数据挖掘的人才会买这本书。换句话说,两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度,因此,我们可以基于物品的流行度对热门物品进行一定的惩罚:
得到用户之间的兴趣相似度后,UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的物品。如下的公式度量了UserCF算法中用户u对物品i的感兴趣程度:
其中,S(u, K)包含和用户u兴趣最接近的K个用户,N(i)是对物品i有过行为的用户集合,wuv是用户u和用户v的兴趣相似度,rvi代表用户v对物品i的兴趣。
3.2基于物品的协同过滤算法(ItemCF)
UserCF在一些网站(如Digg)中得到了应用,但该算法有一些缺点。首先,随着网站的用户数目越来越大,计算用户兴趣相似度矩阵将越来越困难,其运算时间复杂度和空间复杂度的增长和用户数的增长近似于平方关系。其次,基于用户的协同过滤很难对推荐结果作出解释。因此,著名的电子商务公司亚马逊提出了另一个算法——基于物品的协同过滤算法。
基于物品的协同过滤算法(简称ItemCF)给用户推荐那些和他们之前喜欢的物品相似的物品。 比如,该算法会因为你购买过《数据挖掘导论》而给你推荐《机器学习》。不过,ItemCF算法并不利用物品的内容属性计算物品之间的相似度,它主要通过分析用户的行为记录计算物品之间的相似度。该算法认为,物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品B。(个人感觉只是最终的关注点不一样了,还是基于用户啊。。。)
基于物品的协同过滤算法主要分为两步。
(1) 计算物品之间的相似度。
(2) 根据物品的相似度和用户的历史行为给用户生成推荐列表。
ItemCF的第一步是计算物品之间的相似度,在网站中,我们经常看到这么一句话:Customers Who Bought This Item Also Bought,那么从这句话的定义出发,我们可以用下面的公式定义物品相似度:
这里,分母|N(i)|是喜欢物品i的用户数,而分子是同时喜欢物品i和物品j的用户 数。因此,上述公式可以理解为喜欢物品i的用户中有多少比例的用户也喜欢物品j。但是却存在一个问题。如果物品j很热门,很多人都喜欢,那么Wij就会很大,接近1。因此,该公式会造成任何物品都会和热门的物品有很大的相似度,这对于致力于挖掘长尾信息的推荐系统来说显然不是一个好的特性。为了避免推荐出热门的物品,可以用下面的公式:
这里由于还是0-1的原因,我们的余弦相似度可以写成上面的形式。但是,是不是每个用户的贡献都相同呢? 假设有这么一个用户,他是开书店的,并且买了当当网上80%的书准备用来自己卖。那么,他的购物车里包含当当网80%的书。假设当当网有100万本书,也就是说他买了80万本。从前面对ItemCF的讨论可以看到,这意味着因为存在这么一个用户,有80万本书两两之间就产生了相似度。这个用户虽然活跃,但是买这些书并非都是出于自身的兴趣,而且这些书覆 盖了当当网图书的很多领域,所以这个用户对于他所购买书的两两相似度的贡献应该远远小于一个只买了十几本自己喜欢的书的文学青年。因此,我们要对这样的用户进行一定的惩罚,John S. Breese在论文1中提出了一个称为IUF(Inverse User Frequence),即用户活跃度对数的倒数的参数,他也认为活跃用户对物品相似度的贡献应该小于不活跃的用户,他提出应该增加IUF参数来修正物品相似度的计算公式:
在得到物品之间的相似度后,ItemCF通过如下公式计算用户u对一个物品j的兴趣:
这里N(u)是用户喜欢的物品的集合,S(j,K)是和物品j最相似的K个物品的集合,wji是物品j和i的相似度,rui是用户u对物品i的兴趣。
3.3UserCF和ItemCF的比较
首先我们提出一个问题,为什么新闻网站一般使用UserCF,而图书、电商网站一般使用ItemCF呢?
首先回顾一下UserCF算法和ItemCF算法的推荐原理。UserCF给用户推荐那些和他有共同兴 趣爱好的用户喜欢的物品,而ItemCF给用户推荐那些和他之前喜欢的物品类似的物品。从这个算法的原理可以看到,UserCF的推荐结果着重于反映和用户兴趣相似的小群体的热点,而ItemCF的推荐结果着重于维系用户的历史兴趣。换句话说,UserCF的推荐更社会化,反映了用户所在的小型兴趣群体中物品的热门程度,而ItemCF的推荐更加个性化,反映了用户自己的兴趣传承。在新闻网站中,用户的兴趣不是特别细化,绝大多数用户都喜欢看热门的新闻。个性化新闻推荐更加强调抓住新闻热点,热门程度和时效性是个性化新闻推荐的重点,而个性化相对于这两点略显次要。因此,UserCF可以给用户推荐和他有相似爱好的一群其他用户今天都在看的新闻,这样在抓住热点和时效性的同时,保证了一定程度的个性化。同时,在新闻网站中,物品的更新速度远远快于新用户的加入速度,而且对于新用户,完全可以给他推荐最热门的新闻,因此UserCF显然是利大于弊。
但是,在图书、电子商务和电影网站,比如亚马逊、豆瓣、Netflix中,ItemCF则能极大地发挥优势。首先,在这些网站中,用户的兴趣是比较固定和持久的。一个技术人员可能都是在购买技术方面的书,而且他们对书的热门程度并不是那么敏感,事实上越是资深的技术人员,他们看的书就越可能不热门。此外,这些系统中的用户大都不太需要流行度来辅助他们判断一个物品的好坏,而是可以通过自己熟悉领域的知识自己判断物品的质量。因此,这些网站中个性化推荐的 任务是帮助用户发现和他研究领域相关的物品。因此,ItemCF算法成为了这些网站的首选算法。 此外,这些网站的物品更新速度不会特别快,一天一次更新物品相似度矩阵对它们来说不会造成太大的损失,是可以接受的。同时,从技术上考虑,UserCF需要维护一个用户相似度的矩阵,而ItemCF需要维护一个物品相似度矩阵。从存储的角度说,如果用户很多,那么维护用户兴趣相似度矩阵需要很大的空间,同理,如果物品很多,那么维护物品相似度矩阵代价较大。
下表是对二者的一个全面的比较:
4.隐语义模型
隐语义模型是最近几年推荐系统领域最为热门的研究话题,它的核心思想是通过隐含特征 (latent factor)联系用户兴趣和物品。
使用隐语义模型的基本思路是:对于某个用户,首先得到他的兴趣分类,然后从分类中挑选他可能喜欢的物品。那么这个方法大概需要解决三个问题:
1、如何给物品进行分类?
2、如何确定用户对哪些类的物品感兴趣,以及感兴趣的程度?
3、对于一个给定的类,选择哪些属于这个类的物品推荐给用户,以及如何确定这些物品在一个类中的权重?
隐含语义分析技术从诞生到今天产生了很多著名的模型和方法,其中和该技术相关且耳熟能详的名词有pLSA、LDA、隐含类别模型(latent class model)、隐含主题模型(latent topic model)、 矩阵分解(matrix factorization)。这些技术和方法在本质上是相通的,其中很多方法都可以用于个性化推荐系统。我们将以LFM为例介绍隐含语义分析技术在推荐系统中的应用。
LFM通过如下公式计算用户u对物品i的兴趣:
这个公式中pu,k和qi,k是模型的参数,其中pu,k度量了用户u的兴趣和第k个隐类的关系,而qi,k度量了第k个隐类和物品i之间的关系。那么,下面的问题就是如何计算这两个参数。
对最优化理论或者机器学习有所了解的读者,可能对如何计算这两个参数都比较清楚。这两个参数是从数据集中计算出来的。要计算这两个参数,需要一个训练集,对于每个用户u,训练集里都包含了用户u喜欢的物品和不感兴趣的物品,通过学习这个数据集,就可以获得上面的模型参数。我们可以通过最小化下面的损失函数来得到最合适的p和q:(感觉有点神经网络的意思了)
上面的式子中,后面的两项是为了防止过拟合的正则化项,求解上面的式子可以使用随机梯度下降来得到,这里就不再赘述。
LFM模型在实际使用中有一个困难,那就是它很难实现实时的推荐。经典的LFM模型每次训练时都需要扫描所有的用户行为记录,这样才能计算出用户隐类向量(pu)和物品隐类向 量(qi)。而且LFM的训练需要在用户行为记录上反复迭代才能获得比较好的性能。
5.基于图的模型
用户行为很容易用二分图表示,因此很多图的算法都可以用到推荐系统中。
下图是一个简单的用户物品二分图模型,其中圆形节点代表用户,方形节点代表物品,圆形节点和方形节点之间的边代表用户对物品的行为。比如图中用户节点A和物品节点a、b、d相连,说明用户A对物品a、b、d产生过行为。
在得到二分图之后,推荐的任务就变为度量用户顶点vu和与vu没有边直接相连的物品节点在图上的相关性,相关性越高的物品在推荐列表中的权重就越高。图中两个顶点的相关性主要取决于下面三个因素:
1、两个顶点之间的路径数;
2、两个顶点之间路径的长度;
3、两个顶点之间的路径经过的顶点。
基于上面3个主要因素,本节介绍的是一种基于随机游走的PersonalRank算法:假设要给用户u进行个性化推荐,可以从用户u对应的节点vu开始在用户物品二分图上进行随机游走。游走到任何一个节点时,首先按照概率α决定是继续游走,还是停止这次游走并从vu节点开始重新游走。如果决定继续游走,那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点。这样,经过很多次随机游走后,每个物品节点被访问到的概率会收敛到一个数。最终的推荐列表中物品的权重就是物品节点的访问概率。如果将上面的描述表示成公式,可以得到如下公式: