关于 Javascript 尾调用优化的错误论证

最近在研究 JS 调用栈原理时，发现网上用于说明尾调用优化的部分例程不太恰当，缺乏说服力，接下来我会用大量的例子来印证我的看法。先容我简单介绍下相关概念知识。

调用栈（ call stack ）

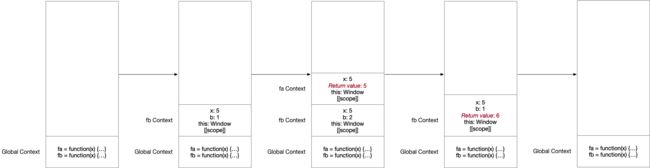
JS 代码在执行时都有其所在的执行上下文，而调用栈就是用于管理这些执行上下文的（每个压入调用栈的执行上下文也称为 调用帧），其管理流程大致如下：

1. 首先，JS 引擎在开始解释执行代码时会先创建一个全局执行上下文并压入调用栈中；
2. 每当有函数被调用时，引擎会为该函数创建一个新的执行上下文并压入调用栈的栈顶，该函数执行完成后，其对应的执行上下文就会从调用栈中弹出；
3. 整个 JS 程序执行结束后，全局执行上下文弹出，调用栈被清空；

// call stack demo
function fa(x) {
  return x;
}

function fb(x) {
  const b = 1;
  return fa(x) + b;
}

console.log(fb(5));

fb(5);    // 6

call stack demo 调用栈操作

PS: 对于每个执行上下文，都包含三个重要属性： 变量对象、作用域链 和 this，详细分析请看 JavaScript深入之执行上下文。

尾调用及尾调用优化

尾调用就是某个函数的最后一步操作是调用另一个函数并返回。想仔细了解哪些表达式和写法属于尾调用，可以看看这篇 Tail call optimization in ECMAScript 6。

我们改造一下上面的 demo 使其属于尾调用：

// call stack demo 的尾调用改造
function fa(x, y) {
  return x + y;
}

function fb(x) {
  const b = 1;
  return fa(x, b);    // 
}

console.log(fb(5));

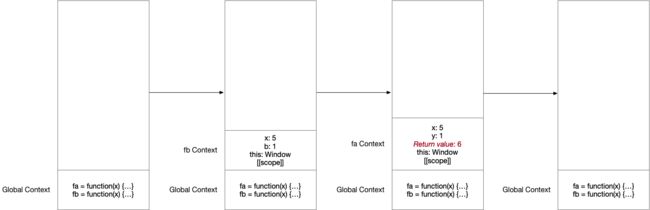
由于 fa 函数执行所需要的 x 和 b 变量都已传递给 fa 的执行上下文，不需要沿着作用域链在 fb 的执行上下文中查找任何变量值；另外 fb 函数的最后一步操作仅仅是返回 fa 函数的返回值，完全可以把 fb 的返回位置直接设为 fa 的返回位置，从而在调用 fa 时就弹出 fb 的执行上下文，这就是 尾调用优化。可见尾调用优化是需要 JS 引擎配合进行的。

尾调用改造后的调用栈操作

尾调用优化可以使递归产生的调用栈零增长，避免出现调用栈过长占用太多内存甚至堆栈溢出的问题。

尾递归论证误区

尾递归就是尾调用函数本身。网上经常使用斐波拉契数列的例子来说明尾递归：

// 非尾递归的斐波拉契数列
function fib(n) {
  return n <= 1 ? 1 : fib(n - 1) + fib(n - 2);
}

fib(100);    // 真的会堆栈溢出么？

事实是，chrome 控制台并没有扔出堆栈溢出的错误，而是程序一直在执行直至页面无响应！。我们来单步 debug 看看 fib函数的执行流程，以 fib(4) 为例：

如图，fib 函数的所有执行上下文可以绘成一颗二叉树，且执行顺序按照二叉树的先序遍历，根据调用栈的原理，fib 函数的部分执行上下文在执行过程中就已经从调用栈中弹出！譬如，在 fib(0) 叶子结点执行完成后，fib(0) 和 fib(2) 都会被弹出调用栈，所以该递归在 n = 100 的量级不会导致堆栈溢出，只会因为函数调用次数过多而程序无响应。

我们看看 chrome 浏览器大概的调用栈长度是多少：

// 获取调用栈深度
function getDeep() {
  try {
    return 1 + getDeep();
  } catch(e) {
    return 1;
  }
}

getDeep();    // 12507

而 fib(40) 的时候 fib 函数到底被调用了多少次呢？

// 计算fib执行次数
let count = 0;
function fib(n) {
  count++;
  return n <= 1 ? 1 : fib(n - 1) + fib(n - 2);
}

fib(40);    // 165580141
console.log(count);    // 331160281

结果是 fib(40) 能成功地执行完，花费了 1864ms。如果 fib 函数的执行上下文是线性关系的话，按照这个调用次数应该早已经堆栈溢出了；另外，fib(40) 的结点数已经达到了 331160281 个，根据二叉树的特性，fib(100) 的结点数将会非常庞大，程序超时也是理所当然了。

那么按照 12507 的堆栈来算，n 为多少时 fib 函数会堆栈溢出呢？可见fib(n) 的二叉树深度为 n，所以 n >= 12507 时就会直接堆栈溢出。其实由于 fib 执行上下文中需要储存一定的变量对象和作用域链，以及受到 JS 内存回收周期的影响，n = 11000 时就已经堆栈溢出了。

因此，斐波那契数列的例子用于说明尾递归并没有代表性，甚至还会造成一定的干扰。有人或许会问，怎么解释斐波拉契数列的尾递归写法确实能优化执行效率？其实只是其尾递归写法大大减少了函数的调用次数，从而避免程序超时而已，本应该堆栈溢出的还是得堆栈溢出......

// 尾递归的斐波拉契数列
let count = 0;
function fib(n, ac1 = 1, ac2 = 1) {
 count++;
 return n <= 1 ? ac2 : fib(n - 1, ac2, ac1 + ac2);
}


try {
 fib(40);    // 165580141
 console.log(count);    // 40
} catch(e) {
 console.log(count);
}

try {
 fib(10000);    // 堆栈溢出  
 console.log(count);
} catch(e) {
 console.log(count);    // 7339
}

同样是 n = 40，非尾递归版本的 fib 函数被调用了 331160281 次，而尾递归版本只被调用了 40 次，对于程序执行效率的优化不言而喻了；但 n = 10000时，依然是 Maximum call stack size exceeded。

PTC（proper tail calls）现状

我们看看各平台对于尾调用优化的支持程度：

桌面浏览器除了 Safari 之外一致飘红，我们在 Safari 中跑一下这个尾递归demo：

// 尾调用优化只会出现在严格模式中
'use strict';

function factorial(n, r = 1) {
  return n === 1 ? r : factorial(n - 1, n * r);
}

factorial(100000);    // Infinity

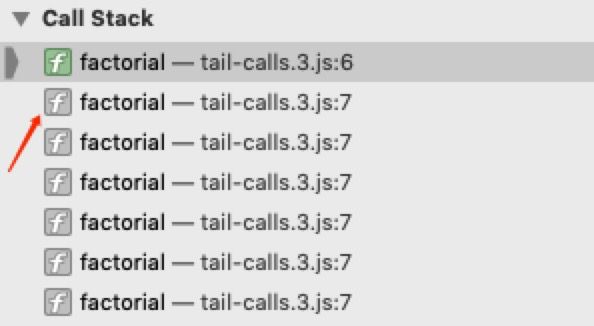
我们看看 Safari 控制台的 Call Stack 信息：

可以看出断点之前创建的调用帧的状态都已被置灰，也就是已经被弹出调用栈，所以说引擎是有进行尾递归优化的。

PS：Safari引擎在这里应该使用了影子堆栈（shadow stack）来恢复已被删除的调用帧。

PTC 带来的问题

实际上，V8 引擎已经实现了尾调用优化，但是默认不开启，可以看看 V8 blog 里这篇文章 ES2015, ES2016, and beyond 的解释。V8 的这个做法是有原因的，PTC会带来一些问题：

1. 由于尾调用优化是隐式的，开发者很难辨别到底哪个函数被尾调用优化了，如果开发者写了一个尾调用的死循环递归，引擎将不会抛出堆栈溢出异常，线程被阻塞。

2. 调用栈信息丢失，开发者在断点调试时会难以理解不连续的堆栈信息；另外一些通过 Error.stack 或者 console.trace 收集异常的工具收集到的信息量将会非常少，看看下面的demo：

'use strict';    // 非严格模式可以关闭尾调用优化

function fa() {
  throw new Error();
}

function fb() {
  return fa();
}

fb();

没有尾调用优化的堆栈信息

尾调用优化的堆栈信息

Syntactic Tail Calls (STC)

为了解决上述的问题，V8 团队提出了语法级尾调用（STC）的提案，定义一种特殊语法 return continue 来告知引擎是否需要开启尾调用优化。详细提案可以看这里 Syntactic Tail Calls (STC)。

不幸的是，该提案目前已经被 TC39 置于 Inactive Proposals 中（提案被遗弃），看来尾调用优化的浏览器实现已经遥遥无期了。

替代方案

递归函数都可以通过循环来实现，但在很多场景下递归改循环并不是一件容易的事，这里提供一种折中方案 蹦床函数：

// 蹦床函数
function trampoline(f) {
  while (f && f instanceof Function) {
    f = f();
  }
  return f;
}

function factorial(n, r = 1) {
  return n === 1 ? r : factorial.bind(null, n - 1, n * r);
}

trampoline(factorial(100000));    // Infinity

蹦床函数其实只是递归改循环的一种跳板工具，需要注意的是，蹦床函数会带来一定的性能额外开销，而且需要对目标函数作侵入式修改，会影响程序可读性。但相较于手动改循环带来的开发难度和 bug 风险，蹦床函数不失为一种很好的选择。

本文涉及的所有例程都已放在 Github 上，欢迎大家交流探讨。

Reference

• Using trampolines to manage large recursive loops in JavaScript
• Tail call optimization in ECMAScript 6
• ECMAScript 6 入门