字符串的全排列
题目描述:
输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c 所能排列出来的所有字符串:
abc、acb、bac、bca、cab 和 cba。
分析和解法:
这是典型的递归求解问题,递归算法有四个特性:
- 必须有可达到的终止条件,否则程序陷入死循环
- 子问题在规模上比原问题小
- 子问题可通过再次递归调用求解
- 子问题的解应能组合成整个问题的解
解法一:递归实现
对于字符串的排列问题:
如果能生成n-1个元素的全排列,就能生成n个元素的全排列。对于只有一个元素的集合,可以直接生成全排列。所以全排列的递归终止条件很明确,只有一个元素时。我们可以分析一下全排列的过程:
- 首先,我们固定第一个字符a,求后面两个字符bc的排列
- 当两个字符bc排列求好之后,我们把第一个字符a和后面的b交换,得到bac,接着我们固定第一个字符b,求后面两个字符ac的排列
- 现在是把c放在第一个位置的时候了,但是记住前面我们已经把原先的第一个字符a和后面的b做了交换,为了保证这次c仍是和原先处在第一个位置的a交换,我们在拿c和第一个字符交换之前,先要把b和a交换回来。在交换b和a之后,再拿c和处于第一位置的a进行交换,得到cba。我们再次固定第一个字符c,求后面两个字符b、a的排列
- 既然我们已经知道怎么求三个字符的排列,那么固定第一个字符之后求后面两个字符的排列,就是典型的递归思路了
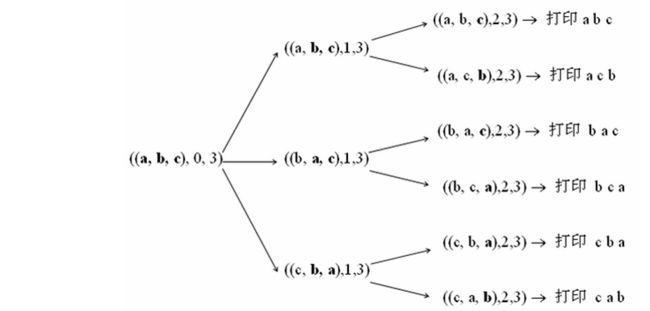
下面这张图很清楚的给出了递归的过程:
源代码如下:
#include
#include
using namespace std;
void AllPermutation(char* perm, int from, int to)
{
if(from > to)
return;
if(from == to) //打印当前排列
{
static int count = 1; //局部静态变量,用来统计全排列的个数
cout << count++ << ":" << perm;
cout << endl;
}
if(from < to) //用递归实现全排列
{
for(int j = from; j <= to; j++) //第j个字符分别与它后面的字符交换就能得到新的排列
{
swap(perm[j], perm[from]);
//cout<<0;
AllPermutation(perm, from + 1, to);
//cout<<1;
swap(perm[j], perm[from]);
//cout<<2;
}
}
}
int main()
{
char str[100];
cin >> str;
AllPermutation(str, 0, strlen(str) - 1);
return 0;
}
但是如果输入里有重复字符又该如何去掉呢?
由于全排列就是从第一个数字起,每个数分别与它后面的数字交换,我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这两个数就不交换了。例如abb,第一个数与后面两个数交换得bab,bba。然后abb中第二个数和第三个数相同,就不用交换了。但是对bab,第二个数和第三个数不同,则需要交换,得到bba。由于这里的bba和开始第一个数与第三个数交换的结果相同了,因此这个方法不行。
换种思维,对abb,第一个数a与第二个数b交换得到bab,然后考虑第一个数与第三个数交换,此时由于第三个数等于第二个数,所以第一个数就不再用与第三个数交换了。再考虑bab,它的第二个数与第三个数交换可以解决bba。此时全排列生成完毕!
这样,我们得到在全排列中去掉重复的规则:
去重的全排列就是从第一个数字起,每个数分别与它后面非重复出现的数字交换。
源代码如下:
#include
#include
using namespace std;
//在[from, to]区间中是否有字符与下标为from的字符相等
bool IsSwap(char* from, char* to)
{
char* p;
for(p = from; p < to; p++)
{
if(*p == *to)
return false;
}
return true;
}
void AllPermutation(char* perm, int from, int to)
{
if(from > to)
return;
if(from == to) //打印当前排列
{
static int count = 1; //局部静态变量,用来统计全排列的个数
cout << count++ << ":" << perm;
cout << endl;
}
if(from < to) //用递归实现全排列
{
for(int j = from; j <= to; j++) //第j个字符分别与它后面的字符交换就能得到新的排列
{
if(IsSwap((perm + j), (perm + to)))
{
swap(perm[j], perm[from]);
//cout<<0;
AllPermutation(perm, from + 1, to);
//cout<<1;
swap(perm[j], perm[from]);
//cout<<2;
}
}
}
}
int main()
{
char str[100];
cin >> str;
AllPermutation(str, 0, strlen(str) - 1);
return 0;
}
分析:时间复杂度为O(n!)。这个解法不难想到,但是需要注意去除重复的那块处理,用最后一位与前面的每个字符比较,如果相等,就不交换,否则交换。
解法二:字典序排列
首先,咱们得清楚什么是字典序。根据维基百科的定义:给定两个偏序集A和B,(a,b)和(a′,b′)属于笛卡尔集 A × B,则字典序定义为
(a,b) ≤ (a′,b′) 当且仅当 a < a′ 或 (a = a′ 且 b ≤ b′)。
所以给定两个字符串,逐个字符比较,那么先出现较小字符的那个串字典顺序小,如果字符一直相等,较短的串字典顺序小。例如:abc < abcd < abde < afab。
那有没有这样的算法,使得
- 起点: 字典序最小的排列, 1-n , 例如12345
- 终点: 字典序最大的排列,n-1, 例如54321
- 过程: 从当前排列生成字典序刚好比它大的下一个排列
答案是肯定的:有,即是STL中的next_permutation算法。
在了解next_permutation算法是怎么一个过程之前,咱们得先来分析下“下一个排列”的性质。
- 假定现有字符串(A)x(B),它的下一个排列是:(A)y(B’),其中A、B和B’是“字符串”(可能为空),x和y是“字符”,前缀相同,都是A,且一定有y > x。
- 那么,为使下一个排列字典顺序尽可能小,必有:
- A尽可能长
- y尽可能小
- B’里的字符按由小到大递增排列
现在的问题是:找到x和y。怎么找到呢?咱们来看一个例子。
比如说,现在我们要找21543的下一个排列,我们可以从左至右逐个扫描每个数,看哪个能增大(至于如何判定能增大,是根据如果一个数右面有比它大的数存在,那么这个数就能增大),我们可以看到最后一个能增大的数是:x = 1。而1应该增大到多少?1能增大到它右面比它大的那一系列数中最小的那个数,即:y = 3,故此时21543的下一个排列应该变为23xxx,显然 xxx(对应之前的B’)应由小到大排,于是我们最终找到比“21543”大,但字典顺序尽量小的23145,找到的23145刚好比21543大。
由这个例子可以得出next_permutation算法流程为:
next_permutation算法
- 定义
- 升序:相邻两个位置ai < ai+1,ai 称作该升序的首位
- 步骤(二找、一交换、一翻转)
- 找到排列中最后(最右)一个升序的首位位置i,x = ai
- 找到排列中第i位右边最后一个比ai 大的位置j,y = aj
- 交换x,y
- 把第(i+ 1)位到最后的部分翻转
还是拿上面的21543举例,那么,应用next_permutation算法的过程如下:
- x = 1;
- y = 3
- 1和3交换,得23541
- 翻转541,得23145
23145即为所求的21543的下一个排列。
源代码如下:
#include
#include
#include
#include
using namespace std;
//反转区间
void Reverse(char* begin, char* end)
{
while(begin < end)
swap(*begin++, *end--);
}
//下一个排列
bool NextPermutation(char* str)
{
assert(str); //检查空指针
char *p, *q, *pFind;
char *pEnd = str + strlen(str) - 1;
if(str == pEnd)
return false;
p = pEnd;
while(p != str)
{
q = p;
p--;
if(*p < *q) //找升序的相邻两数,前一个数即替换数
{
//从后向前找比替换点大的第一个数
pFind = pEnd;
while(*pFind <= *p)
--pFind;
swap(*p, *pFind);
//替换点后的数全部反转
Reverse(q, pEnd);
return true;
}
}
//如果没有找到下一个排列,全部反转后返回false
Reverse(str, pEnd);
return false;
}
int cmp(const void *a,const void *b)
{
return int(*(char *)a - *(char *)b);
}
int main()
{
char str[100];
cin >> str;
int count = 1;
qsort(str, strlen(str), sizeof(char), cmp);
do
{
cout << count++ << ":" << str << endl;
}while(NextPermutation(str));
return 0;
}
分析: 时间复杂度为O(n!)。这个版本是可以有重复字符的。
特别注意:
- 一定要注意边界条件和判断条件,到底是 > 还是 >= ,会影响结果。
参考资料:《编程之法》The Art of Programming By July
字符串的全排列和组合算法