版权声明:本文为博主原创文章,未经博主允许不得转载。
Pythagoras theorem(勾股定理)
一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。 如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达:
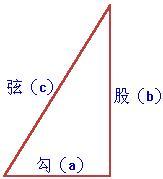
a2+b2=c2
满足这个等式且没有公因数的的三元数组(a,b,c)称为勾股数。 可证a、b两个数必然一奇一偶,证明如下: 如果数a,b都是奇数,则数c必为偶数。可设a=2x+1,b=2y+1,c=2z,有
(2x+1)2+(2y+1)2=(2z)2
展开化简得到下式:
2x2+2x+2y2+2y+1=2z2
上式左边为奇数,右边为偶数,等式显然不成立; 如果数a,b都是偶数,意味着c也是偶数。此时a,b,c都可以被2整除,此时a,b,c不互质。 证毕。 ———-
定理
由 a2+b2=c2 可得 a2=(c−b)(c+b)
假设存在一个数d是(c-b),(c+b)的公因数,即d可以整除(c-b)和(c+b),则d也可以整除
(c+b)+(c-b)= 2c 与 (c+b)-(c-b)= 2b
故d整除2b和2c.而b、c没有公因数,因为我们假设(a,b,c)为本原勾股数组,可以得出d一定是1或2。但d也整除 (c+b)(c−b)=a2 且a为奇数,所以d只能为1,所以(c-b),(c+b)没有公因数。
现在我们知道c-b与c+b没有公因数且 a2=(c−b)(c+b) ,所以c-b,c+b的积是平方数,当且仅当c-b和c+b本身都是平方数。记
c+b=s2 , c−b=t2
其中 s>t⩾1 为没有公因数的奇数。关于b和c解方程组得
c=s2+t22 , b=s2−t22
于是 a=(c+b)(c−b)−−−−−−−−−−−√=st
所以有以下定理
Pythagorean Triples Theorem:
We will get every primitive Pythagorean triple(a,b,c) with a odd and b even by using the formulas:
a=st , b=s2−t22 , c=s2+t22 ( s>t⩾1 )
通过这个公式,取不同s,t的值便可生成不同的勾股数。
下表为 s⩽9 的所有勾股数
| s | t | a=st | b=s2−t22 | c=s2+t22 |
|---|---|---|---|---|
| 3 | 1 | 3 | 4 | 5 |
| 5 | 1 | 5 | 12 | 13 |
| 7 | 1 | 7 | 24 | 25 |
| 9 | 1 | 9 | 40 | 41 |
| 5 | 3 | 15 | 8 | 17 |
| 7 | 3 | 21 | 20 | 29 |
| 7 | 5 | 35 | 12 | 37 |
| 9 | 5 | 45 | 28 | 53 |
| 9 | 7 | 63 | 16 | 65 |