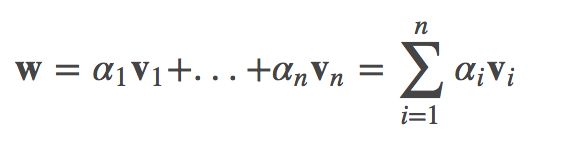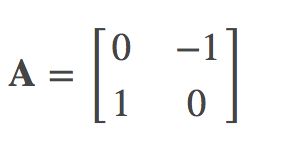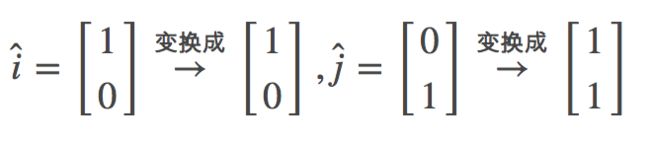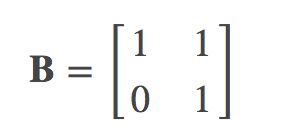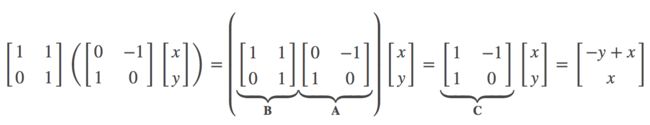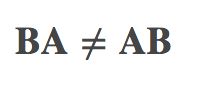本文为原创文章,欢迎转载,但请务必注明出处。
上文介绍从运动的角度直观的理解向量,这一节主要介绍线性变换及其与矩阵的关系。
线性代数的核心之一是线性变换,英文是linear transformation。变换(transformation)可以理解为一个函数(function) f(x),对于线性代数来说,函数的输入就是一个向量,而输出则是变换后的向量。一种理解这种”向量的函数“的方法是使用运动,即用”运动“的思维来思考”变换“。当输入是一个向量,经过变换后的输出是另一向量,相当于这个输入向量移动到了对应的输出向量位置。从系统整体上来考虑,变换可以看成将每一个输入向量都移动到了对应输出向量的位置。比如在平面(二维空间)上,每一点(即每一个向量)经过变换都被移动到了对应的其他位置。
变换包括线性变换和非线性变换,这些变换可以对空间里的对象(即向量)进行升降维,缩放,旋转,平移和扭曲。比如,在神经网络中常见的是输入向量加权后再加上偏移量,最后放到激活函数里,即
其中,W 是神经网络中某一层的权重矩阵,b 是该层上每个神经元的偏移向量, σ(⋅) 是激活函数。于是,W⋅x 可以看成是使用权重矩阵 W 对输入向量 x 进行里变换,变换的结果是对输入向量进行了降维,缩放或旋转(即线性变换);而加上偏移向量 b 就是对线性变换结果 W⋅x 进行了平移 (其实 W⋅x+b 就是仿射变换(affine tranformation));而激活函数 σ(⋅) 的运用就是对结果进行扭曲、挤压和变形(非线性变换),很有意思吧。
回过头来,上面说了变换既是函数又是运动,这个怎么理解呢?其实我们的高等数学因为引入极限的概念研究的就是”运动的数学“ [1]。既然是运动,那么就一定有方向和大小,这就是为什么向量可以求导,为什么用梯度下降算法求最小值时需要沿着负梯度方向更新,这些在后面会介绍。
1、线性变换
在这里我们只关注线性变换,直观上线性变换需要满足两个条件[4]:
- 直线在变换后仍然保持为直线,不能有所弯曲;
- 原点必须保持固定,即线性变换前后原点的位置保持不变。
对于第1条,比如在直角坐标系中虽然变换后的坐标线是直线,原点也没变化,但是坐标上的刻度间隔距离发生变化,导致原坐标系里的对角线在变换后发生了弯曲,这样的变换也不是线性变换。也就是说,线性变换是”保持网格线平行且同一个方向上(如x-轴方向或y-轴方向)等距分布“的变换[4],如图二。如果1满足,2不满足,则是仿射变换 affine transform,在计算机图形学中常用。
好了,到这里在直观上已经对线性变换有了直观的了解:线性变换就是空间中的向量从一个位置运动到另一个位置。那么如何来描述这个运动呢?
2、用矩阵描述线性变换
线性变换是空间中向量的线性运动(沿着直线移动),那么这种向量的直线移动该如何度量呢,怎样从数学上来描述这种移动?前面我们说了要从系统整体上来考虑,变换可以看成将每一个输入向量都移动到了对应输出向量的位置。注意,这里说的是空间中的每一个输入向量的移动都考虑进来。而第一节中我们介绍了空间是基向量的张成,也就是说空间中的每一个输入向量都可以用基向量线性表示。所以,我们只需要对空间中的基向量进行相应的线性变换,然后变换后的向量就可以用这个变换后的基向量进行线性组合。
回忆在第一节时候我们介绍了向量的线性组合如下:
由于线性组合可以用矩阵与向量的乘积表示,于是假设矩阵 A=[v1 … vn], 即矩阵 A 的列是由向量 v1 … vn 组成,那么上式可以表示成:
其中,
我们回到线性变换,我们刚刚说了”变换后的向量可以用这个变换后的基向量进行线性组合“,那么就是说我们可以用变换后的基向量来作为矩阵 A 的列,这个时候矩阵 A 乘以任意输入向量就可以得到变换后的输出向量(比如这里的向量 α 就可以看成是一个输入向量)。到这里,我们将矩阵和线性变换联系起来了,简单总结就是:
- 线性变换就是在空间移动输入向量
- 由于任何向量都可以是空间基向量的线性组合,所以向量的线性变换可以看成两步:首先对基向量进行变换;然后,变换后的基向量进行线性组合得到输出向量。
- 如果一个矩阵 A 的列由变换后的基向量组成,那么矩阵 A 就描述这个线性变换。不同的线性变换规则会得到不同的矩阵,而这些矩阵就是相似矩阵,后面会介绍。
还有一个地方值得说一下,第三节的时候我们在解释张成的时候,我们提到过”缩放基向量再相加“的思想,也就是首先固定基向量,只改变每个基向量的长度进行缩放,然后相加后就可以张成整个空间。而线性变换可以看成是一个相反的运算过程:线性变换首先固定了缩放大小(也就是上面说的输入向量 α ),根据不同的线性变换规则得到变换后的基向量(即基向量变化了,也就是改变基向量的长度和方向),从而得到变换后向输出向量。
在数学计算上,变换后的基向量组成了矩阵 A 的列,他乘以输入向量就得到了输出向量。 我们可以把矩阵 A 左乘向量 x (即 Ax)就看成是向量 x 的一个函数 f(x)。
说到这里还是比较抽象,举例吧(非常重要,下面的例子基于[4])。
首先,平面上直角坐标系的两个标准基向量分别为 î =[1,0]⊤ 和 î =[1,0]⊤,那么对于平面里一个向量 [−1,2]⊤=−1î +2ĵ (即基向量的线性组合,如图三)。
如何对向量 [−1,2]⊤ 进行线性变换呢?然后首先对标准基向量 î 和 ĵ 进行变换等到变换后的基向量,然后对变换后的基向量进行同样线性组合就可以得到变换后的向量(如图四)。这里的”同样线性组合“就是上面说的变换后的基向量进行线性组合时的缩放不变(即仍然是-1和2)。
从这里看出,线性变换首先需要确定的是基向量应该如何变换,即确定矩阵 A。比如这个例子,首先确定标准基向量 î 和 ĵ 的变换方式,即
那么对于任意输入向量 [x,y]⊤ 都可以由变换后的基向量的线性组合得到输入向量:
其中矩阵 A 的列是由变换后的基向量 î 和 变换后的基向量 ĵ 组成。
这就是线性变换!
3、矩阵与矩阵相乘及线性变换复合
为什么有矩阵与矩阵相乘?矩阵与矩阵相乘到底该如何理解?在线性变换里得到了很好的解释。
举个例子(例子来自[4]),比如二维平面中我们首先定义线性变换规则:首先逆时针旋转旋转90度,然后再”剪切(shear)“一次。
首先,基向量 î 和 ĵ 经过逆时针旋转90度后分别变换为:
所以逆时针旋转90度后的”变换矩阵“ A 为:
接着第二步进行”剪切(shear)“,剪切就是保持基向量 î 不变,而 ĵ 旋转到对角线上,即
所以”剪切“变换的”变换矩阵“ B 为:
这个过程下图五所示。
这种分多个不同线性变换步骤后完成的最终的变换就是”线性变换复合(composition)“。具体到这个例子,最终的线性变换就是旋转与剪切两个连续变换的复合,即首先对基向量 î 和 ĵ 进行逆时针90度旋转,得到作为中间结果的变换后的基向量 î 和 变换后的基向量 ĵ ;然后再对这个中间结果的变换后的 î 和 变换后的 ĵ 进行剪切变换,得到最终的的变换后的 î 和 变换后的 ĵ 。
在第一节的时候也提到过”复合“,那么什么是复合呢?复合就是矩阵与矩阵相乘相乘! 很有意思吧,矩阵与矩阵相乘可以看成是把一个线性变换拆成多个步骤,回忆一下,在概率论里我们在求联合概率不也是这样的道理吗?
那么这两个矩阵应该怎么相乘呢?上面我们说到,对向量进行线性变换就是左乘一个矩阵。所以,多个连续的线性变换就是相应的“变换矩阵”按顺序依次左乘! 另外,一个线性变换可以看成是一个函数,那么多个线性变换就可以看成复合函数!
回到上面的例子,假设平面上任意一个向量 [x,y]⊤,对他进行上面的旋转和剪切的线性变换,那么就是依次对该向量左乘矩阵 A 和 矩阵 B:
由于矩阵相乘符合结合律,所以上式可以写成:
上面两个式子的结果完全相同,为什么呢?其实是因为
等式右边的矩阵 C(即复合矩阵)的列刚好分别是基向量 î 和基向量 ĵ 经过逆时针90度旋转和剪切后对应的位置,这也可以看成是基向量 î 和基向量 ĵ 只经过一个步骤就完成了上面需要连续两个步骤才能完成的变换,所以本质上式一样的,所以相等。
这里也可以看出因为先进行逆时针90度旋转再进行剪切得到的线性变换结果,与先进行剪切再进行逆时针90度旋转得到的线性变换结果是不一样的,这就是直观的解释了矩阵与矩阵相乘没有交换律,即
4、相似矩阵
第一节和第三节中我们说过,空间的基向量不是唯一的,即可以同一个空间可以选定不同的基向量(其实空间的基向量确定空间的坐标系。基向量不同,坐标系也不同),那么相同的线性变换就可能有不同的转换矩阵表示形式。那么属于相同线性变换的转换矩阵有什么关系呢?比如乌龟穿上马甲与没穿上马甲都应该是同一个乌龟,不能说穿上了马甲就不认识了。乌龟穿上马甲与没穿上马甲应该是应该是同一个事物的不同表现形式,他们应该是相似的。
相似矩阵就是这个意思,相似矩阵可以看成是同一个线性变换的不同描述,即如果矩阵 A与 B 是同一个线性变换的两个不同的描述,则一定能找到一个非奇异矩阵 P,使得 A与 B 满足[3]:
5、小结
本文介绍了线性变换与矩阵的关系,主要介绍了:
- 矩阵作为向量的线性变换的描述,矩阵左乘向量,其结果就是将向量从一个位置变换(移动)到另一个位置;
- 矩阵作为一组基向量的线性变换的描述,矩阵左乘一个以一组基向量作为列向量的矩阵,就是把线性空间中的一个坐标系(由一组基向量决定)变换到另一个坐标系(由变换后的一组基向量决定)。
References:
- 《重温微积分》,齐民友
- Neural Networks, Manifolds, and Topology
- 理解矩阵
- 3Blue1Brown