该篇文章主要介绍了算法基础以及几种常见的排序算法:选择排序、插入排序、冒泡排序、快速排序、堆排序。
一、算法基础
首先要知道一个算法的好坏主要是从算法的时间复杂度、空间复杂度和稳定性来衡量。
PS: 以下代码主要是用Swift,由于Swift废弃了C的for (i = 1; i< dataArray.count; i++)....形式,考虑到代码的友好性,部分使用OC实现。
时间复杂度
定义: 在进行算法分析时候,语句总的执行次数T(n)是关于问题规模n的函数,进而分型T(n)随着n的变化情况并确定T(n)的数量级.算法的时间复杂度,也就是算法的时间度量记作:T(n)=O(f(n)).它表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称时间复杂度.其中f(n)是问题规模n的某个函数.
时间复杂度是一个函数,它描述了该算法的运行时间,考察的是当输入值大小趋近无穷时的情况。数学和计算机科学中使用这个大 O 符号用来标记不同”阶“的无穷大。这里的无穷被认为是一个超越边界而增加的概念,而不是一个数。
常见的 时间复杂度有O(1)叫常数阶,O(n)叫做线性阶,O(n^2)叫做平方阶 ,当然,还有其他的一些,之后会介绍。计算时间复杂度的过程,常常需要分析一个算法运行过程中需要的基本操作,计量所有操作的数量。
1.用常熟1取代运行时间中的所有加法常数.
2.在修改后的运行次数函数中,只保留最高阶项.
3.如果最高阶项存在且不是1,则去除与这个像相乘的常数.得到的结果就是大O阶.
熟记上述三个步骤,剩下的事就是套用这三句话计算时间复杂度。
1、常数阶
let sum = 0
let n = 100
sum = (1+n)*n/2
print(sum)
上述代码总共执行了四次,一句代码执行一次。那么它的时间复杂度是不是就是4?如果回答是,那就错误了。按照上述的时间复杂度推导大O阶方法来看,第一步的时候要把常数4改为1,再根据2和3部保留最高项。发现根本就没有最高项。所以时间复杂度为O(1)。另外,对于分支结构而言,无论是真还是假,执行的次数都是恒定的,不会随着n的变化而变化,所以单纯的分支接受,其时间复杂度也是O(1)。
2、线性阶
线性阶最具典型的例子就是迭代。例如遍历数组的中的每一个元素。整个遍历过程总时间和数组的长度呈正比(线性增长)。
3、对数阶
var count = 1
while count < n {
count = count * 2
}
上述代码中不难法相,当count大于等于n的时候,整个循环就结束了。可以看出再次之前,循环执行次数符合:2^x=n这个公式,x=log2n。所以上述代码的时间复杂度为O(logn)。
4、平方阶
平方阶就不做过多解释,简单想象for循环嵌套for循环便理解了。
5、时间复杂度效率比较
除了上述所说的时间复杂度,下表中展示了其他一些时间复杂度,以及这些时间复杂度之间的比较。
想O(n^3)、O(n!)等这样的时间复杂度,过大的n会使算法变得不现实,都是时间的噩梦,所以这种不切实际的复杂度,一般都不会去考虑这样的算法。
空间复杂度
和时间复杂度一样,有 O(1),O(log n),O(n),O(n log n),O(n^2),等等。实际写代码的过程中完全可以用空间来换取时间。比如判断2017年之前的某一年是不是闰年,通常可以使通过一个算法来解决。但还有另外一种做法就是将2017年之前的闰年保存到一个数组中。如果某一年存在这个数组中就是闰年,反之就不是。一般来说时间复杂度和空间复杂度是矛盾的。到底优先考虑时间复杂度还是空间复杂度,取决于实际的应用场景。
稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,ri = rj,且 ri 在 rj 之前,而在排序后的序列中,ri 仍在 rj 之前,则称这种排序算法是稳定的;否则称为不稳定的。
二、常见的排序算法
冒泡排序
冒泡排序是一种非常简单的排序算法,几行代码就能实现。但是这里会对最基本的冒泡排序进行一次优化,提升算法效率。
冒泡排序是一种交换排序,记得基本思想是:两两比较相邻记录的关键字,如果反序则交换,直到没有反序位置。先来看一下最基本的冒泡。
1、初级的冒泡排序
//初级版冒泡排序
var array = [9,1,5,8,3,7,4,6,2]
for i in 0.. array[j]{
let temp = array[i]
array[i] = array[j]
array[j] = temp
}
}
}
print(array)
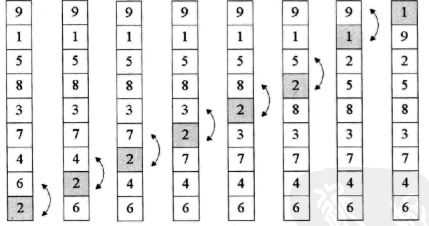
严格意义来说,这段代码不是标准的冒泡排序算法,因为不满足“两两比较相邻记录”的冒泡排序思想,应该是最简单的交换排序。执行过程就是,让每一个关键字都和候命的作对比,如果大就交换。这样第一位置的关键字在一次i循环之后变成最小值。过程如下图:
i=0时,9和1交换后,1和其余关键字比较均最小,因此1放在首位。i=1时,9和5,5和3,3和2交换,最终2放在第二位。
代码简单易懂,但是有缺陷。仔细馆擦在排序好1和2的位置后,对其余关键字的排序并没有什么帮助。
2、冒泡排序初级优化
看看正宗的冒泡排序是如何写的。
//初级优化版冒泡排序
var array = [9,1,5,8,3,7,4,6,2]
for i in 0.. array[j]{
let temp = array[i]
array[i] = array[j]
array[j] = temp
}
}
}
print(array)
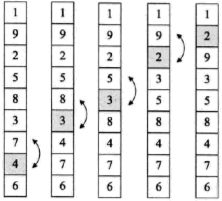
当i=0时,j从9反向循环到1的位置,逐个比较,将较小值交换到前面,知道最后找到最小值放置在第0位置上。
在i等于0的时候最小值1冒泡到最顶端。初次之外,2从最后一位提到了下标为2的位置。
I
i=1的时候,2冒泡到下标为1的位置。除此之外4和3的位置都有所提升。
3、冒泡排序总结
最好的情况下,即待排序的数组本身是有序的,比较的次数是 n-1 次,没有数据交换,时间复杂度为O(n)。最坏的情况下,即待排序的数组是完全逆序的情况,此时需要比较 n*(n-1)/2 次。因此时间复杂度是O(n^2)。
选择排序
炒股票的人通常分为两种,一种是买菜大妈,总是不断的买进卖出,通过差价专区盈利。但通常这种人获利不会太多。还有一种炒股老手,不买则已,一买便惊人,通常会以较少的交易次数最终收益甚佳。如果说冒泡排序是炒股中的买菜大妈,则选择排序就是炒股中的老手。
1、选择排序的实现
选择排序的基本思想就是通过 n-i 次关键字之间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i个记录做交换,而不是像冒泡排序那样,每一次比较之后,符合条件的都做一次交换。选择排序相对于冒泡排序做的交换次数更少,具体实现请看下面代码。
var array = [9,1,5,8,3,7,4,6,2]
var min = 0
for i in 0..2、选择排序总结
注意简单选择排序中的数据交换是放在第一层for循环内部,当寻找到目标下标才进行数据交换。而冒泡排序的数据交互是放在第二层for循环内,因此排序相同的数据冒泡执行的交换次数会大于或等于选择排序。但是通过仔细分析时间复杂度可以得出,无论是在最好还是最差的情况下,比较的次数都是n*(n-1)/2。所以选择排序的时间复杂度也是O(n^2)。虽然和冒泡排序的时间复杂度相等,但简单选择排序在性能上要略微优于冒泡排序。
插入排序
每次将一个待排序的关键字,按照其大小插入到前面已经排好序的子序列中的恰当位置,直到所有关键记录插入完成为止,这就是插入排序的基本思想。
1、插入排序实现
由于Swift中废弃了C语言for循环这种形式:for (i = 1; i< dataArray.count; i++)....。感觉如果使用Swift的for循环实现如下的插入排序算法非常不友好,所以这里使用了OC实现该算法。使用何种语言这里不做深究,最重要的是理解这种排序思想。
NSMutableArray *dataArray = [NSMutableArray arrayWithArray:@[@9,@1,@5,@8,@3,@7,@4,@6,@2]];
int i,j;
NSNumber *temp = [[NSNumber alloc]init];//哨兵
for (i = 1; i< dataArray.count; i++) {
//判断当前的下标i的数组元素是否大于下标i-1的数组元素,如果大于,就执行以下操作
if (dataArray[i]= 0 && dataArray[j] > temp; j--) {
dataArray[j+1] = dataArray[j];
}
dataArray[j+1] = temp;
}
}
NSLog(@"%@",dataArray);
1、首先取第一个元素,默认该元素已经按照大小顺序排列在子序列中。
2、判断当前的下标 i 的数组元素是否大于下标 i-1 (已经排好的子序列最大下标)的数组元素,如果大于,就执行之后的操作。
3、如果符合上述 2 条件,就取出下一个元素(已经排序好的子序列最大下标 +1 的元素 ),在已经排序的元素序列中从后向前扫描。
4、如果该元素(已排序)大于新元素,将该元素移到下一位置。重复此步骤,直到找到已排序的元素小于或者等于新元素的位置。并将新元素插入到该位置后。
5、重复 2 - 5 步骤。
2、插入排序总结
最好的情况下,完全没有任何数据移动,时间复杂度是O(n)。最坏的情况下,比较的次数为 (n+2) * (n-1)/2,移动的次数最大值为(n+4) * (n-1)/2。如果按照序列的好坏程度是随机的,且概率都是相同的,则平均比较次数以及平均移动次数都约为 n^2/4次,所以时间复杂度为O(n ^ 2)。通过和冒泡以及简单选择排序对比,不难看出直接插入排序的性能稍微比前两者好上一些。
快速排序
快速排序算法是前面所讲的最慢的冒泡排序算法升级,都属于交换排序(即通过不断的比较和移动交换实现排序)。只不过,快速排序的脚步跨度比冒泡排序要大的多,将关键字从最前面移动到最后面或从最后面移动到最前面。从而在整体上减少了总的比较次数和移动交换次数。
1、快速排序实现
通过一趟排序将数据分割成独立的两部分,其中一部分的关键字均比另外一部分的关键字小。对被分割的这两个部分再做同样的操作,直到不能被分割位置,此时整个序列就变成有序的数列。
fileprivate func quickSort( _ array:inout [Int],start:Int,end:Int){
/*如果左边索引大于等于右边的索引代表排序完成*/
if start >= end{
return
}
//var array = array
//从数组中挑选出一个元素,作为“基准”
let mid = array[end]
var left = start
var right = end - 1
while (left < right){
//从左边开始找,找到大于mid的数就停止
while (array[left] < mid && left < right){ left += 1 }
//从右边开始找,找到小于mid的数就停止
while (array[right] >= mid && right > left){ right -= 1 }
//交换left和right
let temp = array[left]
array[left] = array[right]
array[right] = temp
}
//使left对应的数小于左边的数,大于右边的数
if array[left] >= array[end] {
//交换left和end
let temp = array[end]
array[end] = array[left]
array[left] = temp
}else {
left += 1
}
//递归执行,将基准左边两边的数,按照上面的形式再次拆分执行
quickSort(&array, start: start, end: left - 1)
quickSort(&array, start: left + 1, end: end)
}
//调用形式
var array = [9,1,5,8,3,7,4,6,2]
self.quickSort(&array, start: 0, end: array.count-1)
print(array)
1,在数组中选取一个关键字,称之为枢轴(pivot),作用就是以这个枢轴为基准,把数组分为两部分,枢轴左边的值全部比枢轴的值小,右边比其小。这里选择数组中的最后一个元素当作这个数组的枢轴。
2,重排数列,所有比基准小的放在基准前面,比基准大的放在最后。和基准大小相同的数字可以放到任意一边。分区结束后,基准就处于数列中间。对这一步骤具体的来说:为了减少一些没有必要的移动,选择最后一个元素作为基准,剩下的元素中寻找左边比基准大的,右边比基准小的,满足条件就交换位置,最后两端汇聚在一起。这种汇聚分为两种情况:左端汇集到右端或右端汇集到左端。从左到右汇集这种情况,说明汇集之前左边比基准小,如果右边交换过则右边比基准大,所以左右两端汇集时交换左端和基准即可。如果右边没有交换过,大于基准值就交换左端和基准值,小于就去掉基准值,继续快排。 右端汇集到左端,说明左端找到了比基准大的值,右端比基准大,此时只要将左端和基准交换即可。
2、快速排序总结
快排的时间复杂度为时间复杂度 O(n log n)。最差情况,递归调用 n 次,即空间复杂度为 O(n)。最好情况,递归调用 log n 次,空间复杂度为 O(log n),空间复杂度一般看最差情况,时间可以平均,但空间一定得满足,所以空间复杂度为 O(n)。
堆排序
1、堆的概念
在讲堆排序之前,首先需要介绍堆的概念。堆和二叉树是有一定的关联性,堆是具有下列性质的完全二叉树:每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆。或者每个节点的值都小于或等于其左右孩子节点的值,称为小顶堆,如下图。
堆可以通过数组形式实现,下图是一个数组,最上面的是根节点,每个父节点有两个子节点。并且满足这样一个规律:
- 1、父节点 i 的做节点为 2 * i + 1;
- 2、父节点的右节点为 2 * i + i;
- 3、子节点 i 的父节点在 (i - 1)/2 (该数值要向下取整)。
2、堆排序实现思路
堆排序就是利用堆进行排序,这里假设是利用大顶堆。基本思想是将带排序的序列构造成一个大顶堆,整个序列的最大值就是堆顶的根节点。将根节点移走(实际上是将根节点和堆数组最末尾的元素进行交换,此时末尾的元素即为最大值),然后将剩余的 n - 1个序列重新构造成一个堆,这样就会得到整个序列的第二大值。反复这样执行,便能得到一个有序序列。
明白了堆排序的思想,便可知道实际上堆排序主要是解决两个问题:
- 1、如果将一个数组构建成为一个堆数组?
- 2、如何在输出堆顶元素后,调整剩余的元素为一个新的堆数组?
3、堆排序实现
var array = [9,1,5,8,3,7,4,6,2]
for i in (0...(array.count/2 - 1)).reversed(){
maxHeap(&array, start: i, end: array.count)//形成最大堆
}
//将堆顶的最大数放到最后,再将前面的元素重新调整,得到最大堆。此时将最大的数放置到倒数第二位置,如此反复执行
for i in (1...(array.count - 1)).reversed(){
let temp = array[0]
array[0] = array[i]
array[i] = temp
maxHeap(&array, start: 0, end: i)//形成最大堆
}
print(array)
上述代码中总过分为两个for循环。第一个for循环就是将现在的待排序序列构建为一个最大堆,也就是maxHeap()函数的任务。第二个for循环就是逐步将每个最大值的根节点和末尾元素进行交换,然后再调整为最大堆。下面是maxHeap函数实现代码。
fileprivate func maxHeap(_ array:inout [Int],start:Int,end:Int){
var dad = start
var son = dad * 2 + 1
while son < dad {
//比较左右子节点的大小
if son + 1 < end && array[son] < array[son+1]{
son += 1
}
//如果父节点大于子节点,直接return
if array[dad] > array[son] { return }
//如果父节点小于子节点,交换父子节点,因为子节点变了,所以子节点可能比孙节点小,需继续比较
let temp = array[dad]
array[dad] = array[son]
array[son] = temp
dad = son
son = dad * 2 + 1
}
}
maxHeap 函数中应用到了上面提到的父节点和子节点的下标计算公式。该函数主要是使一个数列形成最大堆。先比较两个子节点的大小,找到最大的子节点同根比较。如果根节点大则已经是最大堆;如果根节点小,则交换子节点和根节点的关键字,此时子节点还要保证以它自己为根节点的堆为最大堆,所以要同孙节点做比较。。。。
4、堆排序总结
在构建堆的过程中,由于是是完全二叉树从最下层最右边非终端节点开始构建,将它与子节点进行比较,对于每个费终端节点而言,最多进行两次比较和交换操作,因此构建堆的时间复杂度为O(n)。在整个排序过程中,第 i 次去堆顶记录重建堆需要时间为logi ,并且需要取 n - 1次堆记录,所以重建对的时间复杂度为O(nlogn)。所以对的时间复杂度为O(nlogn)。
空间上只需一个暂存单元。由于记录的比较是跳跃进行的,所以堆排序是一种不稳定的排序。最后要提醒一点,由于初始构建堆的所需的比较次数比较多。所以,一般不适合排序个数较少的数组。
博文总结
除了上述所说的选择排序、插入排序、冒泡排序、快速排序、堆排序这些比较常见的排序方式,还有其他一些排序方法如归并排序、希尔排序、基数排序等。没有十全十美的排序算法,各有优点和缺点。即使所谓的快速排序,也只是总的来看比较好,但是也存在不稳定、需要大量暂存空间、比较少量数据无优势。程序员的世界中不应该只是API的调用,还要有逻辑。算法很美很优雅,你要控制尼支及,不然一不小心就被它吸引了,然后来个方向转换。