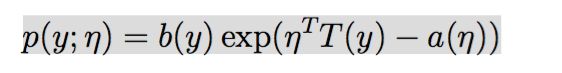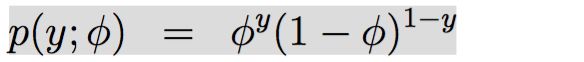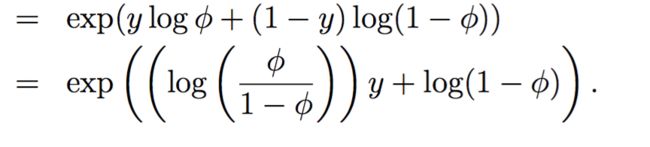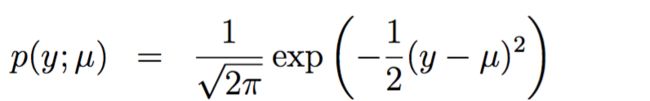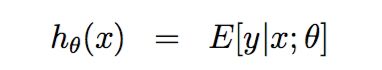广义线性模型、指数分布族中的高斯分布、伯努利分布

姓名：崔少杰学号：16040510021

转载自：http://www.jianshu.com/p/d1b7ca81d1af=有修改

【嵌牛导读】：广义线性模型、指数分布族中的高斯分布、伯努利分布

【嵌牛鼻子】：广义线性模型、指数分布族、高斯分布、伯努利分布

【嵌牛提问】：为什么要有指数分布族？

【嵌牛正文】：定义指数分布族：（指数分布族的定义符号有很多版本，这里采用的是CS229 描述的写法，注意PRML的写法稍有不同，CS229是斯坦福大学Andrew NG的机器学习课程，PRML是模式识别机器学习的经典书籍）

指数分布族形式

η 是自然参数（natural parameter，also called thecanonical parameter）。

T(y) 是充分统计量（sufficient statistic），一般情况下就是y。

a(η) 是对数部分函数（log partition function），这部分确保Y的分布p(y:η) 计算的结果加起来（连续函数是积分）等于1.

伯努利分布作为指数分布族的例子（比如在某段时间内，广告被点击的分布；某段时间内，顾客是否进店等等）：

设均值（mean)为 φ,分布在Y上的取值为{0,1}，因此

p(y= 1;φ) =φ;

p(y= 0;φ) = 1−φ

即，调整φ,得到不同的伯努利分布，一旦设定好φ，T,a,b都被固定住，就能得到一个伯努利分布。

如

伯努利分布

把上式的右边改写成指数分布族形式

指数分布族形式

可以看出，

b(y) = 1

T(y) = y

a(η) = -log(1−φ)

η = log (φ/(1-φ))

因此 φ=

这个就是sigmoid函数了，也是logistic 函数，Great.

高斯分布作为指数分布族的例子（线性回归 linear regression）：

假设 σ^2 = 1

(注：If we leaveσ2as a variable, the Gaussian distribution can also be shown to be in the)

exponential family, whereη∈R2is now a 2-dimension vector that depends on bothμandσ. For the purposes of GLMs, however, theσ2parameter can also be treated by considering

a more general definition of the exponential family:p(y;η, τ) =b(a, τ) exp((ηTT(y)−a(η))/c(τ)). Here,τis called thedispersion parameter, and for the Gaussian,c(τ) =σ2;

but given our simplification above, we won’t need the more general definition for the

examples we will consider here.） From CS229 lecture notes。