【r<-高级|理论|分类】逻辑回归、决策树、随机森林

有监督学习基于一组包含预测变量和输出变量的样本单元。将全部数据分为一个训练数据集和一个验证数据集，其中训练集用于建立预测模型，验证集用于测试模型的准确性。

这部分通过rpart、rpart.plot和party包来实现决策树模型及其可视化，通过randomForest包拟合随机森林，通过e1071包构造支持向量机，通过R中的基本函数glm()实现逻辑回归。在探索之前，先安装好相应的包。

pkgs <- c("rpart", "rpart.plot", "party",
          "randomForest", "e1071")
install.packages(pkgs, dependencies = TRUE)

这里的例子来源于UCI机器学习数据库中的威斯康星州乳腺癌数据。数据分析的目的是根据细胞组织细针抽吸活检所反应的特征，来判断被捡者是否患有乳腺癌。

数据准备

该数据集是逗号分隔的txt文件，包含699个样本蛋白，其中458个良性，241个为恶性。数据集中有11个变量，表中未标明变量名。其中16个样本单元中有缺失数据并用问号（?）表示。

变量为

ID
肿块厚度
细胞大小的均匀性
细胞形状的均匀性
边际附着力
单个上皮细胞的大小
裸核
乏味染色体
正常核
有丝分裂
类别

ID不纳入数据分析，最后一个变量是输出变量（良性=2，恶性=4）。

对于每一个样本来说，另外九个变量是与判别恶性肿瘤相关的细胞特征，并加以记录。这些细胞特征得分为1（最接近良性）到10（最接近病变）之间的整数。任一变量都不能单独作为判别良性或恶性的标准，建模的目的是找到九个细胞特征的某种组合，从而实现对恶性肿瘤的准确预测。

## Data preparation
loc <- "http://archive.ics.uci.edu/ml/machine-learning-databases/"
ds  <- "breast-cancer-wisconsin/breast-cancer-wisconsin.data" 
url <- paste(loc, ds, sep="")

breast <- read.table(url, sep = ",", header = FALSE, na.strings = "?")
names(breast) <- c("ID", "clumpThickness", "sizeUniformity", "shapeUniformity",
                   "maginalAdhesion", "singleEpithelialCellSize", "bareNuclei",
                   "blandChromatin", "normalNucleoli", "mitosis", "class")
df <- breast[-1]
df$class <- factor(df$class, levels = c(2,4),
                   labels = c("benign", "malignant"))


set.seed(1234)
train <- sample(nrow(df), 0.7*nrow(df))
df.train <- df[train,]
df.validate <- df[-train,]
table(df.train$class)
table(df.validate$class)

逻辑回归

逻辑回归是广义线性模型的一种，它根据一组数值变量预测二元输出（之前在广义模型中有介绍）。基本函数glm()可以用于拟合逻辑回归模型。

## logistic regression
fit.logit <- glm(class ~ ., data=df.train, family=binomial()) # 拟合逻辑回归
summary(fit.logit)                            #　检查模型

Call:
glm(formula = class ~ ., family = binomial(), data = df.train)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-2.75813  -0.10602  -0.05679   0.01237   2.64317  

Coefficients:
                          Estimate Std. Error z value Pr(>|z|)    
(Intercept)              -10.42758    1.47602  -7.065 1.61e-12 ***
clumpThickness             0.52434    0.15950   3.287  0.00101 ** 
sizeUniformity            -0.04805    0.25706  -0.187  0.85171    
shapeUniformity            0.42309    0.26775   1.580  0.11407    
maginalAdhesion            0.29245    0.14690   1.991  0.04650 *  
singleEpithelialCellSize   0.11053    0.17980   0.615  0.53871    
bareNuclei                 0.33570    0.10715   3.133  0.00173 ** 
blandChromatin             0.42353    0.20673   2.049  0.04049 *  
normalNucleoli             0.28888    0.13995   2.064  0.03900 *  
mitosis                    0.69057    0.39829   1.734  0.08295 .  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1


prob <- predict(fit.logit, df.validate, type="response")　　#　建立预测模型,对训练集集外样本单元分类
logit.pred <- factor(prob > .5, levels=c(FALSE, TRUE),
                     labels = c("benign", "malignant"))　　
logit.perf <- table(df.validate$class, logit.pred,
                    dnn=c("Actual", "Predicted"))　　　　　　# 评估预测准确性
logit.perf

           Predicted
Actual      benign malignant
  benign       118         2
  malignant      4        76

predict()函数默认输出肿瘤为恶性的对数概率，指定参数type="response"即可以得到预测肿瘤为恶性的概率。在样本单元中，概率大于.5的被分为恶性肿瘤类，概率小于等于.5的被分为良性肿瘤类。

最后给出预测与实际情况对比的交叉表（混淆矩阵，confusion matrix）。数据集中有１０个单元包含缺失数据而无法判别。

在验证集上，正确分类的模型（准确率，accuracy）为(76+118)/200=97%。看起来还是非常准确的哈～

值得注意的是，模型中有三个预测变量的系数未能通过显著性检验，一般而言可以将它们去除从而精简模型。

当然，可以用逐步逻辑回归生成一个包含更少解释变量的模型，其目的是通过增加或移除变量来得到一个更小的AIC值。例如本例可以用

logit.fit.reduced <- step(fit.logit)来得到一个更为精简的模型。

决策树

决策树是数据挖掘领域中常用模型。其基本思想是对预测变量进行二元分离，从而构造一颗可以预测新样本单元所属类别的树。这里介绍两类决策树：经典树和条件推断树。

这里讲的基本思想有点精悍，似懂非懂的样子。我们具体来看看它们究竟是什么吧。

经典决策树

经典决策树以一个二元输出变量和一组预测变量为基础。其具体算法如下：

选定一个最佳预测变量将全部样本单元分为两类，实现两类中的纯度最大化（即一类中良性样本单元尽可能多，另一类恶性样本单元尽可能多）。如果预测变量连续，则选定一个分割点进行分类，使得两类纯度最大化；如果预测变量为分类变量，则对各类别进行合并再分类。
对每个子类别继续执行步骤1。
重复步骤1~2，直到子类别中所含的样本单元树过少，或者没有分类能将不纯度下降到一个给定阈值以下。最终集中的子类别即终端节点。根据每一个终端节点中样本单元的类别数众数来判别这一终端节点的所属类别。
对任一样本单元执行决策树，得到其终端节点，即可以根据步骤3得到模型预测的所属类别。

这一过程就类似一棵树生长不断形成分支，这些分支的生成是依赖具体的算法要求（这里就是让它们纯度最大化）。

上述算法构建的树过大，容易出现过度拟合现象。可采用10折交叉验证法预测误差最小的树，然后用它进行预测。

R中的rpart包支持rpart()函数构造决策树，prune()函数对决策树进行剪枝。下面给出针对数据集的算法实现。

library(rpart)
set.seed(1234)
dtree <- rpart(class ~ ., data=df.train, method="class",
              parms=list(split="information"))     # 生成树
dtree$cptable

        CP nsplit rel error xerror       xstd
1 0.800000      0   1.00000 1.0000 0.06484605
2 0.046875      1   0.20000 0.2750 0.03954867
3 0.012500      3   0.10625 0.1500 0.02985779
4 0.010000      4   0.09375 0.1625 0.03101007

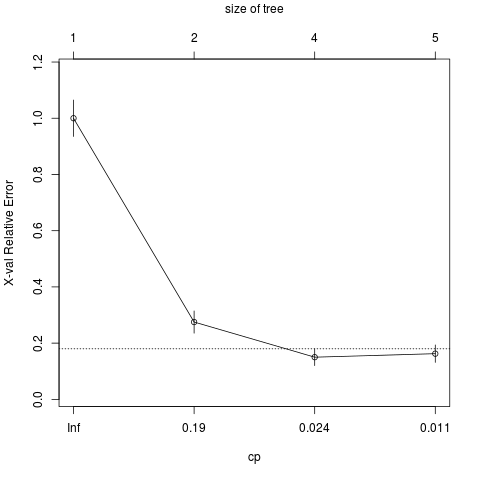
plotcp(dtree)

dtree.pruned <- prune(dtree, cp=.0125)          # 剪枝

library(rpart.plot)

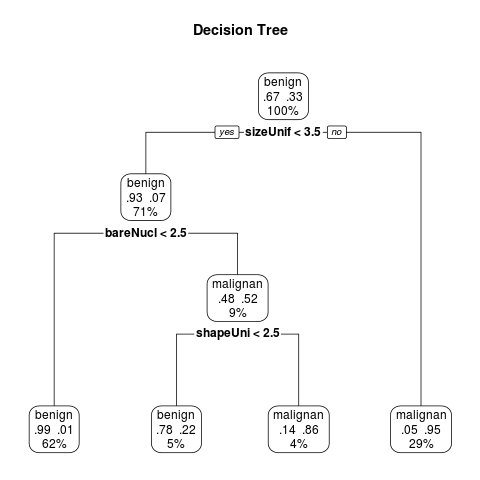
prp(dtree.pruned, type=2, extra=104,
    fallen.leaves = TRUE, main="Decision Tree")

dtree.pred <- predict(dtree.pruned, df.validate, type="class")   # 对训练集外样本单元分类
dtree.perf <- table(df.validate$class, dtree.pred,
                    dnn=c("Actual", "Predicted"))
dtree.perf

           Predicted
Actual      benign malignant
  benign       122         7
  malignant      2        79

dtree.png

rpart()返回的cptable值中包括不同大小的树对应的预测误差，因此可以用于辅助设定最终的树的大小。其中，复杂度参数cp用于惩罚过大的树；树的大小即分支数nsplit，有n个分支的树将有n+1个终端节点；rel error栏即各种训练集中各种树对应的误差；交叉验证误差xerror即基于训练样本所得的10折交叉验证误差；xstd栏为交叉验证误差的标准差。

借助plotcp()函数可画出交叉验证误差与复杂度参数的关系图（上图）。对于所有交叉验证误差在最小交叉验证误差一个标准差范围内的树，最小的树即最优的树。

由代码中的cptable表可以知道，四个终端节点（三次分割）的树满足要求。

deci_tree.png

在完整树的基础上，prune()函数根据复杂度参数减掉最不重要的枝，从而将树的大小控制在理想范围内。从代码中的cptable内容中可以看到，三次分割对应的复杂度参数是0.0125，从而prune(dtree, cp=0.0125)可得到一个理想大小的树。

rpart.plo包中的prp()函数可用于画出最终的决策树，它有很多的可供选择参数，如type=2可画出每个节点下分割的标签，extra=104可画出每一类的概率以及每个节点处的样本占比，fallen.leaves=TRUE可在图的底端显示终端节点。

对观测点分类时，从树的顶端开始，若满足条件则从左枝往下，否则右枝往下，重复这个过程知道碰到一个终端节点为止。该终端节点即为这一观测点的所属类别。

最后predict()函数用来对验证集中的观测点分类。代码内容中给出了实际类别与预测类别的交叉表。整体来看，准确率还是非常高的。

条件推断树

条件推断树与传统决策树类似，但变量和分割的选取是基于显著性检验的，而不是纯净度或同质性一类的度量。显著性检验是置换检验。

条件推断的算法如下：

对输出变量与每个预测变量间的关系计算p值。
选取p值最小的变量。
在因变量与被选中的变量间尝试所有可能的二元分割（通过排列检验），并选取最显著的分割。
将数据集分成两群，并对每个子群重复上述步骤。
重复直至所有分割都不显著或已经达到最小节点为止。

条件推断树可由party包中的ctree()函数获得。

library(party)
fit.ctree <- ctree(class ~ ., data=df.train)
plot(fit.ctree, main="Conditional Inference Tree")

ctree.pred <- predict(fit.ctree, df.validate, type="response")
ctree.perf <- table(df.validate$class, ctree.pred, 
                    dnn=c("Actual", "Predicted"))
ctree.perf

con_infer_tree.png

值得注意的是，对于条件推断树来说，剪枝不是必需的，其生成过程相对更自动化一些。另外，party包也提供了许多图像参数。

随机森林

随机森林是一种组成式的有监督学习方法。在随机森林中，我们同时生成多个预测模型，并将模型的结果汇总以提升分类准确率。http://mng.bz/7Nul上有关于随机森林的详尽介绍。

随机森林的算法涉及对样本单元和变量的抽样，从而生成大量决策树。对每个样本单元来说，所有的决策树依次对其进行分类。所有决策树预测类别中的众数类别即为随机森林所预测的这一样本的类别。

假设训练集中共有N个样本单元，M个变量，则随机森林算法如下：

从训练集中随机有放回地抽取N个样本单元，生成大量决策树。
在每一个节点随机地抽取m
完整生成所有决策树，无需剪枝。
终端节点的所属类别由节点对应的众数类别决定。
对于新的观测点，用所有的树对其进行分类，其类别由多数决定原则生成。

生成树时没有用到的样本点所对应的类别可以由生成的树估计，与其真实类别比较即可得到袋外预测（out-of-bag, OOB）误差。无法获得验证集时，这是随机森林的一大优势。随机森林算法可以计算变量的相对重要程度。

randomForest包中的randomForest()函数可以用于生成随机森林。函数默认生成500棵树，并且默认在每个节点处抽取sqrt(M)个变量，最小节点为1。

library(randomForest)
set.seed(1234)
fit.forest <- randomForest(class ~ ., data=df.train,
                           na.action = na.roughfix,
                           importance = TRUE)   # 生成森林
fit.forest
importance(fit.forest, type=2)    # 给出变量重要性
forest.pred <- predict(fit.forest, df.validate)    # 对训练集外样本进行分类
forest.perf <- table(df.validate$class, forest.pred,
                     dnn = c("Actual", "Predicted"))
forest.perf

几个输出结果

> fit.forest

Call:
 randomForest(formula = class ~ ., data = df.train, importance = TRUE,      na.action = na.roughfix) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 3

        OOB estimate of  error rate: 3.68%
Confusion matrix:
          benign malignant class.error
benign       319        10  0.03039514
malignant      8       152  0.05000000

> importance(fit.forest, type=2)
                         MeanDecreaseGini
clumpThickness                  12.504484
sizeUniformity                  54.770143
shapeUniformity                 48.662325
maginalAdhesion                  5.969580
singleEpithelialCellSize        14.297239
bareNuclei                      34.017599
blandChromatin                  16.243253
normalNucleoli                  26.337646
mitosis                          1.814502

> forest.perf
           Predicted
Actual      benign malignant
  benign       117         3
  malignant      1        79

randomForest()函数从训练集中有放回地随机抽取489个观测点，在每棵树的每一个节点随机抽取3个变量，从而生成了500棵传统决策树。na.action=na.roughfix参数可将数值变量中的缺失值替换成对应列的中位数，类别变量中的缺失值替换成对应列的众数类（若有多个众数则随机选一个）。

随机森林可度量变量重要性，通过设置information=TRUE参数得到，并通过importance()函数输出。由type=2参数得到的变量相对重要性就是分割该变量时节点不纯度（异质性）的下降总量对所有树取平均。节点不纯度由Gini系数定义。本例中，sizeUniformity是最重要的变量，mitosis是最不重要的变量。

randomForest包根据传统决策树生成随机森林，而party包中的cforest()函数可以基于条件推断树生成随机森林。当预测变量间高度相关时，基于条件推断树的随机森林可能效果更好。

相比较于其他分类方法，随机森林的分类准确率通常更高。另外，随机森林算法可处理大规模问题（即多样本单元、多变量），可处理训练集中有大量缺失值的数据，也可以应对变量多于样本单元的数据。可计算袋外预测误差、度量变量重要性也是随机森林的两个明显优势。

随机森林的一个明显缺点是分类方法较难理解和表达。

（关于这一章节的解释比较细致，我也难以精简，保持原文能尽量帮助自己和大家理解。里面确实又涉及到了一些之前没有接触过的概念，因为我暂时也用不到，暂做粗浅理解。大家如果有兴趣，查查查。现在百度看解释和博文已经成为一种习惯了～）

关于后续内容，新知识点比较多，下次整理说明吧。

整理自R实战