序言:红黑树是数据结构与算法中最重要的知识点之一,也是最难掌握的。网上有关它的讨论很多,我曾经试图阅读那些“一篇文章让你熟悉红黑树”之类,可能是智力的缘故,效果平平。最终,我发现要想理解红黑树的特性和相关算法其实并无捷径可走。所以,我打算通过多篇博客来解释这个众所周知却又少有人精通的数据结构——RedBlackBalanceSearchTree。
一、标准二叉树的非理想情况
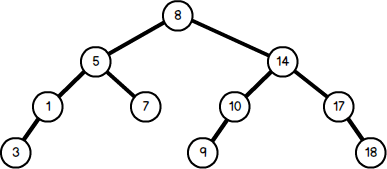
在理想状态下,标准二叉树的结构应该如此:
含有10个节点的二叉树最大命中次数不超过3。但是标准二叉树依赖是依赖输入的,这也就意味着同样的输入形成的结构也可能是这样:
所以,问题就转变成了如何让二叉树的结构不依赖输入,或者说如何让二叉树保持自平衡。
二、2-3查找树
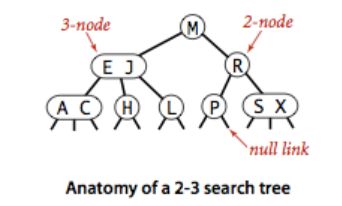
为了保证查找树的平衡,我们需要一些灵活性,因此在这里我们允许树中的一个节点保存多个键。确切的说,我们将一颗标准的二叉查找树中的节点称为2-节点(包含一对自有键值和两条子链接)。而现在我们引入3-节点(包含两对自有键值和3条子链接),同理我们还定义了4-节点。
3-节点的左子树都小于自有键值中的任一键(我们记作<),右子树都大于任一键(我们记作>),中间子树则位于两个自有键之间(我们记作><):
一颗完美的平衡2-3查找树中的所有空连接(null link)到根节点的距离都应该是相同的。
下面我们将看到,如何在向一棵2-3树中插入新键依然能够保持它的平衡(即:2-3树的自平衡特性)。如果我们需要在一个2-节点上挂新键只需要将这个2-节点变成一个3-节点即可:
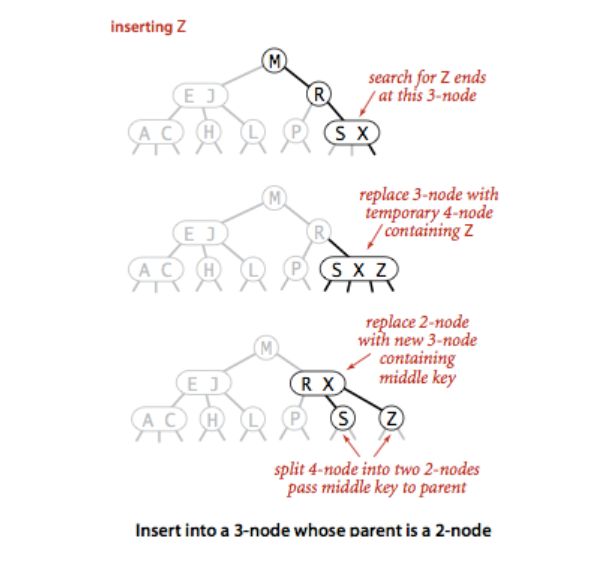
这里演示了如果在2-节点(L)上挂新键(K)。但是如果需要在一个3-节点上挂新键就要麻烦一些,试着按照上图想象一下挂(Z)的情况。
由于我们要挂的地方已经没有空间了,为了将新键插入,我们不妨先临时将新键存入该节点(SX)中,使之成为了一个4-节点(SXZ)。再把它转换成为一颗由3个2-链接组成的2-3树,并把新生成的父节点(X)向上插入。
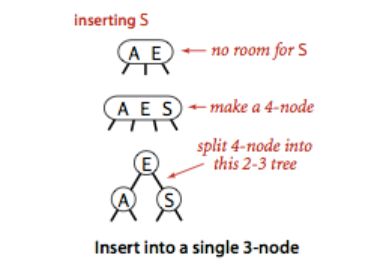
如果向上的过程中遇到的依然是3-节点,我们就以同样的算法分解再向上直到它的根节点。如果到达根节点发现依然是3-节点的情况我们就会分解并产生新的根节点,同时2-3树的高度+1。这是2-3树的一条很重要的性质,它显示了2-3树是如何生长的:
2-3查找树和二叉树的区别之一就是,二叉树是不断向下生长,而2-3树则是向上生长,这个特性保证了2-3树中任一空节点到根节点的距离相等。因此我们认为2-3树的结构不依赖输入并且是自平衡的。
后记:本篇博客应该接在二叉树后阅读,不幸的是有关二叉树的文章我还没有写(咱就是这么任性)。所以如果想读懂本文请先了解二叉树的相关知识或者等我在补齐了其他知识点后再回头来阅读本文。