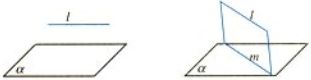平面基本性质
- 连结两点的线中,线段最短
- 过两点有一条直线,并且只有一条直线
公理1
如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内,直线在平面内或平面经过直线
公理2
- 经过不在同一条直线上的三点,有且只有一个平面
- 不共线的三点确定一个平面
公理3
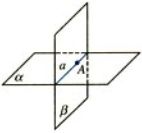
- 如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线
- 称这两个平面相交,这条公共直线叫做这两个平面的交线
平面基本性质的推论
推论1
推论2
推论3
共面,空间中的几个点或几条直线都在同一平面内
空间中的平行关系
平行直线
平行公理(二维) 过直线外一点,有且只有一条直线和这条直线平行
公理4(空间平行线的传递性)
- 平行于同一条直线的两条直线互相平行
- a//b,c//b,那么a//c
定理
如果一个角的两边与另一个角的两边分别对应平行,并且方向相同,那么这两个角相等
空间四边形
顺次连结不共面的四点A、B、C、D所构成的图形
- 空间四边形的对角线,连结不相邻两顶点的线段
- 空间四边形的边,连结相邻顶点间的线段
直线与平面平行
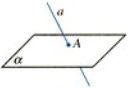
直线a和平面α只有一个公共点A,叫做直线与平面相交,记作a∩α=A
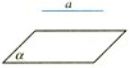
直线a和平面α没有公共点,叫做直线与平面平行,记作a//α
直线与平面平行定理
- 如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行
定理(利用线、面平行判断线、线平行)
- 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和两平面的交线平行
平面与平面平行
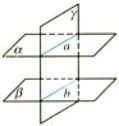
如果两个平面没有公共点,那么这两个平面叫做平行平面,平面α平行于平面β,记作α//β
平面平行的判定定理
定理
如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行
推论
如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,则这两个平面平行
定理
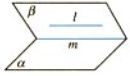
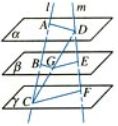
如果两个平行平面同时与第三个平面相交,那么它们的交线平行
两条直线被三个平行平面所截,截得得对应线段成比例
空间中的垂直关系
l是平面α的垂线,α是直线l的垂面,O叫做垂足,垂线段的长度叫做这个点到平面的距离
直线与平面垂直的判定定理
如果一条直线与平面内的两条相交直线垂直,则这条直线与这个平面垂直
推论
如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直于这个平面
定理
两条直线垂直于同一个平面,那么这两条直线平行
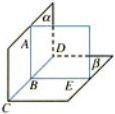
平面与平面垂直
如果两个相交的交线与第三个平面垂直,且这两个平面与第三个平面相交所得的两条交线互相垂直,就称这两个平面互相垂直
平面与平面垂直的判定定理
如果一个平面过另一个平面的一条垂线,则两个平面互相垂直
定理
如果两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面