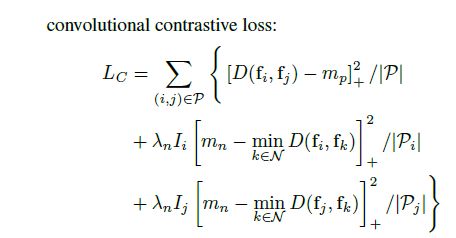一 知识背景
3D scan&cloud points(点云)patch-based features,fully convolutional network, deep metric learning, sparse tensors,sparse convolutions, hard negetive-mining, contrastive loss, triplet loss, batch normalization...
1.cloud points(点云)
“在逆向工程中通过测量仪器得到的产品外观表面的点数据集合也称之为点云,通常使用三维坐标测量机所得到的点数量比较少,点与点的间距也比较大,叫稀疏点云;而使用三维激光扫描仪或照相式扫描仪得到的点云,点数量比较大并且比较密集,叫密集点云,

在稀疏的卷积中和权值${W}$相乘的${x}$必须在${C}$中,这样的系数卷积得到的也是一个稀疏的结果。文中的${V^(3){-1,0,1}}$我觉得其中的元素不必是固定的${{-1,0,1}}$,如果非要是这样,卷积(相关)就无法计算了(这也是我在阅读时遇到的困惑)。当然最主要的还是要在code中去实现这个系数卷积。[接下来的时间我会探索一下]。
文章正文:
从3D扫描或者是点云上提取几何特征是许多工作的第一步。例如注册(registration),重建(reconstruction)和跟踪(tracking)。现今的(state of art)方法需要将低阶(low-level)的特征作为输入来计算。
“低层次特征提取算法基于兴趣点所在表面及临近点的空间分布,提取基本的二维、三维几何属性作为兴趣点特征信息,如线性、平面性等。低层次特征提取算法复杂度低、运算效率高、内存消耗少,但领域尺寸的选择对识别效果影响较大。”
“高层次特征提取算法基于低层次几何特征及临近点空间分布,定义并计算更复杂的几何属性作为特征信息。根据几何属性的定义又可细分为基于显著性、基于直方图、基于显著性直方图与基于其他特征的四大类提取算法[1][2]。”
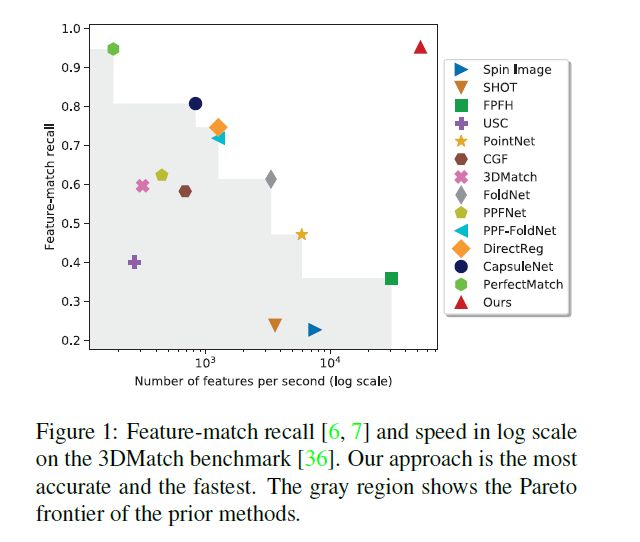
这里说明下指标:recall 中文叫查全率又叫召回率,其计算公式如下:
$recal{l_c} = \frac{{T{P_c}}}{{T{P_c} + F{N_c}}}$
意思是某一类判断正确占到该类总数的百分比。理所当然的想要提升recall可以遵循“宁可错杀一百,不可放过一人”的思想。嘿嘿~
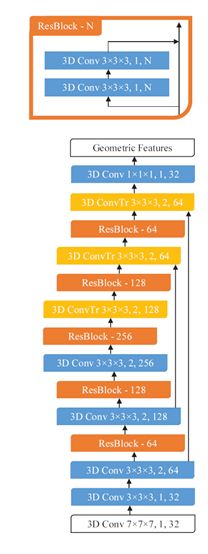
接着我们给出作者用的网络框架:
这是一个ResUNet的架构,两个白框是输入输出层,每个块用三个参数来描述:kernel size, stride, channel dimensionality.(核大小,步幅,和通道维度)除了最后一层其他的卷积层后面都有Batch normalization然后跟一个非线性(Relu).
那说了半天啥是全卷积特征啊?
全卷积特征作者说了:
我给你翻译翻译:
全卷积网络纯粹的由具有平移不变性的操作组成,像卷积和元素级别的非线性。(我不懂啥是元素级别的非线性啊?)同样,我们吧稀疏卷积网络(注这里是因为他用的稀疏卷积所以将这个网络将spase convolution network)给一个稀疏的tensor用上,我们得到的也是个稀疏的tensor,我们把这个稀疏的tensor输出叫做全卷积特征。
OK。
重头戏来了,嘿嘿~
作者自己说自己搞了个新的Metric learning的新的损失函数。在看他的新家伙式儿之前,我们不妨回顾下他站在谁的肩膀上搞了个大新闻。。
在前面的背景知识里有提到,就是negative mining 和标准的metric learning 的损失函数。这个作者说自己用全卷积网络了搞了个metric learning,而且还把negative mining整合到对比损失函数和三元组损失函数里了,他自己把整合后的这个新的损失函数叫做“Hardest contrastive"和”hardest-triplet"
网络:“我太难了(哭腔)"。
好言归正传,想要搞metric learning必须遵循两个约束,一个是类似的特征必须和彼此之间挨的足够近,对于分类来说,肯定是越近越好,那么有
$D({{f}_{i}},{{f}_{j}})\to 0\forall (i,j)\in P$
啥意思?${P}$是正确配对feature-match成功的特征,${(i,j)}$是其中的一个组合。相反的不相似的特征必然挨的越远越好,那我们就给他一个警戒线称之为margin(注:margin在英语里由差距,差额之意)用数学来说就是
$D({{f}_{i}},{{f}_{j}})>m\forall (i,j)\in N$
这里的${D}$是一种距离的衡量手段,原文没说啥距离,我觉得应该可以用欧氏距离。
文章说Lin等人说这些对于正例的约束会导致网络过拟合,然后搞出个针对正例的基于margin的损失函数。式子里右下角的+号代表着大于0时就取这个值,否则就取0。说实话,我因为一直吧这里边的${I_{ij}}$当是个示性函数,以为根据后边中括号里边的东西来取值,一直没搞懂,后来偶来见发现tm这两货是分开的。我真想吐槽这作者。。
作者的对正例加了个margin的约束后,可以解决网络过拟合的现像。
接着又弄个三元组(triplet loss)损失,我一并给出原文,瞅瞅:
在许多的文献了这篇文章后边也用了,这(4)里边的这个${f}$叫做anchor(中文名叫锚)而${f_+}$代表正例里边的元素。带负号的就不难说了。
在negative mining里边就说了,网络的性能会被小部分”人"左右,是谁呢?就是那些对于网络来说非常难啃的硬骨头——“hardest negatives"
接着作者讨论一个容易被人忽视,但却至关重要的存在:全卷积特征的特性
传统的Metric learning 认为特征是独立同分布的(iid),为啥?作者说了:
因为batch是随机采样来的。
这里需要和大家回顾下啥是epoch,batch,iteration
-
epoch:代表在整个数据集上的一次迭代(所有一切都包含在训练模型中);
-
batch:是指当我们无法一次性将整个数据集输入神经网络时,将数据集分割成的一些更小的数据集批次;
-
iteration:是指运行一个 epoch 所需的 batch 数。举个例子,如果我们的数据集包含 10000 张图像,批大小(batch_size)是 200,则一个 epoch 就包含 50 次迭代(10000 除以 200)。
虽说基础,但也要温故而知新嘛~
然而,然而...
在全卷积特征的提取过程中,相邻特征的位置是相关的。
------------------------------------
今天接着写。
昨天夜里回去到b站上一个讲点云的视频,挺有收获的,地址贴出来。
----------------------------------------------
因为全卷积特征的这个相近的特征之间有局部的关联,所以在难例挖掘的时候could(这个翻译成能还是可能?)找到和锚点相近的伪负例(false negatives)[反正我不懂],所以说去除这些个伪负例至关重要。在作者之前的paper里使用了一个distance来约束。
并且作者提到全卷积网络得到的特征比标准尺度学习算法得到的要多几个数量级,全卷积几何特征是~40k个特征仅仅对一对儿扫描(而且这还与batch-size成比例的增加)。
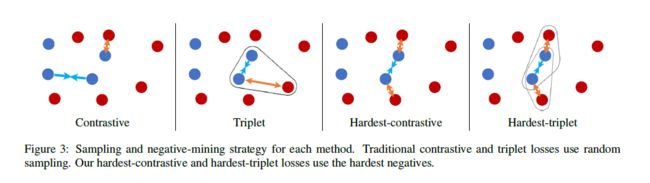
接下来讨论作者的hardest-contrastive和hardest-triplet losses
首先采样一系列的锚点和一个挖掘每个场景的集合。看看原文:
这里看看作者是怎么将难例挖掘整合到对比损失里的:
${P}$是一个minibatch经过全卷积网络提取出来的全部正例,${N}$是一个随机的由该网络卷积得出的特征的一个子集,该子集将会被用来进行难例挖掘。
${I_i}$是一个indicator function,是${I(i,k_{i},d_{t})}$的简写。当特征${f_{k_{i}}}$位于以特征${f_i}$为圆心,直径为${d_t}$的球面外时,为1,反之为0。其中${k_i}$满足:${{k}_{i}}=\arg {{\min }_{k\in N}}D({{f}_{i}},{{f}_{k}})$。
也就是说${{f}_{ki}}$是所有负例里最靠近该正例的。而\[\left| {{P}_{i}} \right|=\sum\nolimits_{(i,j)\in P}{I(i,{{k}_{i}},{{d}_{t}})}\]
表示针对特征$f_i}$的所有合法的负例的个数。可以类推。${{\lambda }_{n}}$是一个权重,将其设置成0.5.这里的${d_t}$就是上文提到的为了除去伪负例而设置的threshold。
类似的我们可以得到triplet loss:
上式确实找到了对于组合${(i,j)}$最难的负例,但是但是这最强的负例却容易collapse。
这里:不用平方损失可以防止特征collapse到一个点。作者的点子又把就是hardest的和随机抽样的triplets都同样的使用的方法加上。
至于具体的代码及实现环节可以去参考paper的原文,及作者的github。
算法的思想到这里就结束了。
这篇paper的两个spotlight:
1.全连接提取特征,拜托了之前的patch-based
2.对metric learning的两个损失函数contrstive 和triplet loss 做了改进。
===================