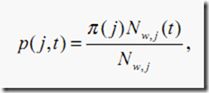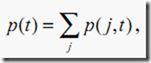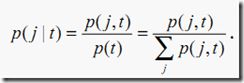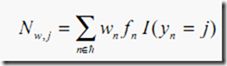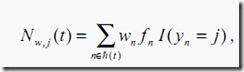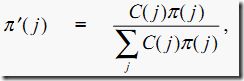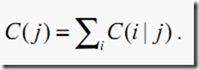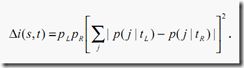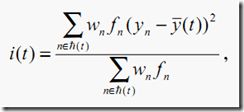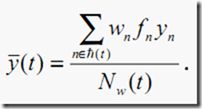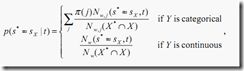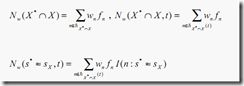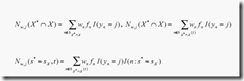说明一些变量的含义
Y
独立变量,或者成为目标变量。可以是离散的(对于分类的情况,代表类标号),也可以是连续的(对于回归的情况,代表函数值)。
如果Y是离散的,且有J个类,它的取值范围为C={1,...,J}
Xm, m = 1, ... M
所有预测变量的集合。每个预测变量可以是离散的,也可以是连续的
整个训练集,供决策树生长使用
落在节点t上的训练样本
wn
关联到样本n的权重
fn
样本n的频数
π(j),j=1,...,J
Y=j, j=1,...,J的先验概率p(Y=j)
p(j,t),j=1,...,J
在节点t中j类中的一个样本的概率
p(t)
一个样本在节点t中的概率
P(j|t),j=1,...,J
落到节点t的j类的一个样本的概率
C(i|j)
把类j的例子错分为类i的例子的代价.显然C(j|j)=0
树生长的过程
算法只考虑单变量的分裂。
1.找到预测变量的最佳分裂点
对于连续和有序的预测变量,从小到大排列它的值。对于排列好的预测变量,从头遍历每个值来检查每个候选分裂点。最好的分裂点最大化分裂准则。
对于名词性的预测变量(如颜色:红、绿、蓝),检查每个可能的子集来获得最好的分裂。
2.找到节点的最佳分裂
在步骤1中发现的最好分裂中,选择一个可以最大化分裂准则的。
3.迭代:使用步骤2找到的最佳分类分裂节点直到停止规则满足
停止规则:
· depth of the tree branch being constructed has reached the specified maximum value.
· 树分支的深度达到了指定的最大值
· number of training samples in the node is less than the specified threshold, when it is not statistically representative to split the node further.
· 落到某个节点的训练样本的数目比指定的阈值还要少,当它已经不具有统计的典型性来进一步分裂节点
· all the samples in the node belong to the same class (or, in the case of regression, the variation is too small).
· 落到该节点的所有样本都同属于相同的类(或者在回归的情况中,变化非常小)
· the best split found does not give any noticeable improvement compared to a random choice.
· 发现的最佳分裂与随机选择的分裂相比没有显著的提升
分类准则和不纯度的估计
在节点t,最好的分类s被选择来最大化一个准则![]() 。当一个节点的不纯度测量被定义,分裂准则用于减小不纯度。
。当一个节点的不纯度测量被定义,分裂准则用于减小不纯度。
分类不纯度
如果Y是离散的情况,有三个不纯度估计的准则:Gini不纯度、Towing不纯度、和有序Twoing不纯度.
在节点t
这里
I(a=b)为指示函数如果a=b则值为1,否则为0
Gini准则
一个节点t的不纯度为
Gini分裂准则对于不纯度的降低被定义为:
这里pL和pR是发送一个样本到左孩子节点tL和右孩子节点tR的概率。它们被估计为pL=p(tL)/p(t)和pR=p(tR)/p(t)。
注意:当用户指定了错分类代价,更改过的先验概率可以用来替换之前的先验概率。如果更改过的先验概率被使用了,那么问题可以看作成没有代价被使用。更改过的先验概率被定义为:
这里
Twoing准则
有序Twoing准则
有序Twoing准则被使用仅当Y是有序离散的。它的算法如下:
1.首先将类C={1,...,J}分成两个超类C1和C2=C-C1,满足C1={1, ..., j1},j1=1, ..., J-1
2.使用类间测量i(t)=p(C1|t)p(C2|t),发现分裂s*(C1)最大化![]() ,
,
回归不纯度
这里
![]()
代理分裂(Surrogate Split)
给定一个分裂X*<=s*,它的代理分裂是一个分裂使用另外一个预测属性X,X<=sX(or X>sX),满足与主分裂最相似并且有着正的关联预测度量(predictive measure of asscoiation)。可以有多个代理分裂。关联预测度量(Predictive measure of association)越大,代理分裂越好。
predictive measure of asscoiation关联预测度量
令![]() 为同时没有缺失X*和X的值的学习样本(resp. 节点t的学习样本)的集合。令
为同时没有缺失X*和X的值的学习样本(resp. 节点t的学习样本)的集合。令![]() 为发送一个在
为发送一个在![]() 中的样本到相同的子节点(同时通过s*和sX判定)的概率,并且
中的样本到相同的子节点(同时通过s*和sX判定)的概率,并且![]() 是最大化概率
是最大化概率![]() 的分裂
的分裂
这里pL(resp. pR)是在节点t的最好的分裂s*发送一个没有缺失X*值的样本到左子树的相对概率,pL=p(tL)/p(t)(resp. pR=p(tR)/P(t) 并且这里
并且如果分裂s*和sX发送样本n到相同的子集![]() 指示函数的值为1,否则0
指示函数的值为1,否则0
处理缺失值
如果样本的目标变量缺失了,这个样本会被忽略。所有的预测属性缺失了,这个样本也会被忽略。如果样本权重和频数缺失了、为0或者为负,样本也被忽略。
代理节点的方法用来处理预测属性的缺失值。假设X*