1. The Lloyd-Max algorithm is hill-climbing algorithm
第六节最后提出一个好的quantizer必须满足Lloyd-Max条件,但满足Lloyd-Max条件的不一定都是最优方案,举个例子:
It can be seen in the figure that the rightmost peak is more probable than the other peaks. It follows that the MSE would be lower if R1 covered the two leftmost peaks. However, in this figure, the two rightmost peaks are both covered by R2, with the point a2 between them. Both the points and the regions satisfy the necessary conditions and cannot be locally improved.
从哪里开始分会得到不同的结果,局部优不代表结果最优。The Lloyd-Max algorithm is a type of hill-climbing algorithm; starting with an arbitrary set of values, these values are modified until reaching the top of a hill where no more local improvements are possible.
2. Vector quantization
As with source coding of discrete sources, we next consider quantizing n source variables at a time. This is called vector quantization, since an n-tuple of rv’s may be regarded as a vector rv in an n-dimensional vector space.
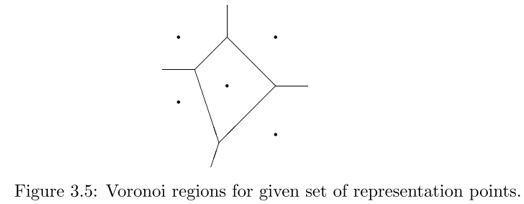
Let (U, U) be the two rv’s being jointly quantized. Since mapping (u, u’) into (aj, aj’) generates a squared error equal to (u−aj )² + (u’−aj’)², the point (aj, aj’) which is closest to (u, u’) in Euclidean distance should be chosen. Consequently, the region Rj must be the set of points (u, u’) that are closer to (aj, aj’) than to any other representation point.
For the given representation points, the regions {Rj} are minimum-distance regions and are called Voronoi regions. The boundaries of the Voronoi regions are perpendicular bisectors(垂直平分线) between neighboring representation points. The minimum-distance regions are thus in general convex polygonal regions(凸多边形), as illustrated in the figure below:
3. Entropy-coded quantization
The minimum expected number of bits per symbol, Lmin, required to encode the quantizer output was shown in Chapter 2 to be governed by the entropy H[V ] of the quantizer output, not by the size M of the quantization alphabet. Therefore, anticipating efficient source coding of the quantized outputs, we should really try to minimize the MSE for a given entropy H[V ] rather than a given number of representation points.
This can be minimized over ∆1 and ∆2 subject to the constraint that M = M1 + M2 = L1/∆1 + L2/∆2. Ignoring the constraint that M1 and M2 are integers (which makes sense for M large), the minimum MSE occurs when ∆i is chosen inversely proportional to the cube root of fi. In other words,
Appendix 3 shows that, in the limit of high rate, the quantization intervals all have the same length! A scalar quantizer in which all intervals have the same length is called a uniform scalar quantizer. The following sections will show that uniform scalar quantizers have remarkable properties for high-rate quantization.
4. High-rate entropy-coded quantization
The quantization regions can be made sufficiently small so that the probability density is approximately constant within each region.
This means that a uniform quantizer can be used as a universal quantizer with very little loss of optimality. The probability distribution of the rv’s to be quantized can be exploited at the level of discrete source coding.
The analogue of the entropy H[X] of a discrete rv is the differential entropy h[U] of an analog rv. After defining h[U],the properties of H[U] and h[U] will be compared.
5. Differential entropy
The differential entropy h[U] of an analog random variable (rv) U is analogous to the entropy H[X] of a discrete random symbol X.