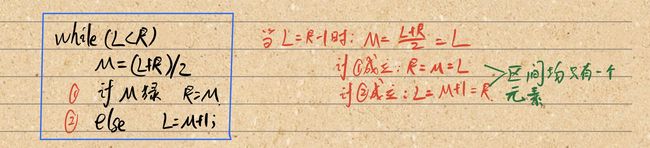基础算法——二分（原理细节与习题归纳整理）

目录：

• 整数二分
• 实数二分
• 相关习题

核心思想：

　　1、确定一个区间，使目标值一定在区间内

　　2、找到一个性质满足：

　　　　（1）具有二段性（即可分成连续的，性质不同的两段，同一段内性质相同）；

　　　　（2）答案是二段性的分界点；

一、整数二分：

　　　简介：

　　　　　　整数二分因为数在数轴上是离散分布（即不是连续的），且int型变量默认向下取整，所以实现的时候

　　　　　　很容易出现死循环的情况。这里给出两类整数二分的实现方法及其相关原理，可以有效避免死循环的情况； 

　　    第一类：

　　　　　　　　

　　　　　　ans（答案）是红色区间的右端点。将【L,R】分成【L,M-1】、【M,R】两个区间。

　　　　　　if M在红色区间内，说明ans必然在【M,R】区间；

　　　　　　else ans必然在【L,M-1】区间；

 　　　　　　例:在单调递增序列a中查找<=x的数中最大的一个（即x或x的前驱）：

　　　　　　　　　if M在红色区间内，说明ans必然在【M,R】区间；

　　　　　　　　　　　　　　　　　　↔ 

　　　　　　　if (mid<=x) mid之前数的都比x小，<=x的最大的数不可能在mid之前，可行区域应缩小为右半段

　　　　　　伪码如图：

　　　　　　　　

　　　　　　　　PS：如上图证明：求M时若不“+1”，当L=R-1且第一个条件满足时，L永远不变，循环无法退出。

　　　　第二类：

　　　　　　　　

　　　　　　　ans是绿色区间的左端点。将【L,R】分成【L,M】、【M+1,R】两个区间。

　　　　　　　if M在绿色区间内，说明ans必然在【L,M】中；

　　　　　　　else ans必然在【M+1,R】中；

　　　　　　伪码如图：

　　　　　　  

　　　　　　　PS：这里求M时无需“+1”，如图证明可知若“+1”当条件一成立时，程序会陷入死循环。

　　　　小结：

　　　　　　整数二分步骤：

1. 1. 1. 找一个区间【L,R】，使得answer一定在该区间内
      2. 找一个判断条件，使得该条件具有二段性，并且答案一定是该二段性的分界点
      3. 分析中点M在该条件下是否成立，
         　如果成立，考虑答案在哪个区间;
         　如果不成立，考虑答案在哪个区间；
      4. if更新方式写的是：
         　R=Mid; 不用任何处理
         　L=Mid; 计算Mid时"+1"

二、实数二分：

　　由于实数在数轴上连续、稠密分布，二分时必然可以求到一个精确的M，不存在整数二分的边界问题。

　　所以实数二分相对比较简单，只要在r-l小于一个足够小的数前，不断二分循环毕竟答案即可。

　　唯一需要注意的地方就是一般为了精确度考虑，二分边界条件精度到问题所求后两位。

　　（如：问题要求保留小数点后6位，设置条件时r-l则大于小数点后8位）

三、相关习题：

　　（前为本人题解链接，后位原题链接）

　　AcWing790. 数的三次方根　　　　　　原题链接　　（实数二分模板题） 

　　AcWing 789. 数的范围   　　  　　　 原题链接　　（整数二分模板题、两类写法均用到）

　　AcWing 1221. 四平方和　　　　　　  原题链接　　 （有多种解法，二分是其中一种）

　　AcWing 730. 机器人跳跃问题 　　　　原题链接