在2018年TensorFlow开发者峰会上,我们宣布了TensorFlow Probability:一种概率编程工具箱,用于机器学习研究人员和其他从业人员快速可靠地利用最先进硬件构建复杂模型。如果出现以下情况,我们推荐你使用TensorFlow Probability:
- 你想建立一个生成数据的模型,并推理其隐藏的过程。
- 你需要量化预测中的不确定性,而不是预测单个值。
- 你的训练集具有大量相对于数据点数量的特征。
- 你的数据是结构化的,例如,使用组、空间、图表或语言语义 - 并且你希望使用先前的信息来捕获此结构。
- 你有一个相反的问题:见TFDS'18谈话:重建测量融合等离子体。
TensorFlow Probability为你提供解决上述这些问题的工具,此外,它还继承了TensorFlow的优势,如自动差异化,以及跨多种平台(CPU,GPU和TPU)扩展性能的能力。
什么是TensorFlow Probability?
我们这次发布的机器学习工具为TensorFlow生态系统中的概率推理和统计分析提供了模块化抽象。
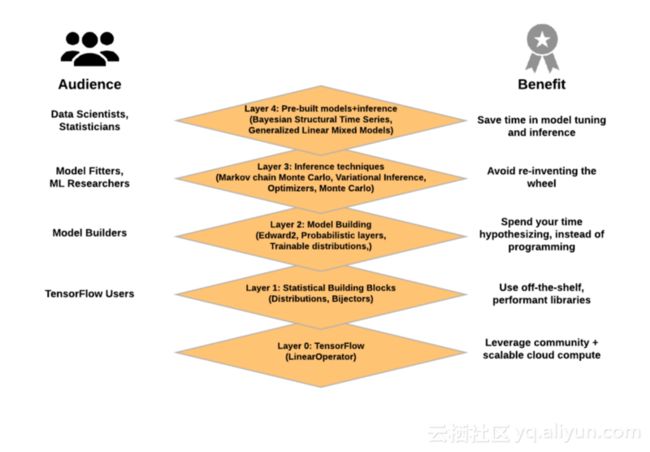
TensorFlow概率的概述。概率编程工具箱为从数据科学家和统计人员到所有TensorFlow用户的用户提供了好处。
第0层:TensorFlow的数值运算。特别是,LinearOperator类实现了无矩阵计算,可以利用特殊结构(对角线,低秩矩阵等)进行高效计算。它由TensorFlow Probability团队构建和维护,现在是TF中tf.linalg核心的一部分。
第1层:统计构建模块
- 分布(tf.contrib.distributions,tf.distributions):一个包含了批量和广播语义的概率分布和相关统计的大量集合。
- Bijectors(tf.contrib.distributions.bijectors):支持随机变量的可逆和可组合变换。Bijectors提供了丰富的变换分布类别,从经典的例子(如对数正态分布)到复杂的深度学习模型(如masked自回归流)。
(有关更多信息,请参阅TensorFlow Distributions白皮书。)
第2层:模型构建
- Edward2(tfp.edward2):一种用于将灵活的概率模型指定为程序的概率编程语言。
- 概率图层(tfp.layers):对其所代表的功能具有不确定性的神经网络图层,扩展了TensorFlow图层。
- 可训练分布(tfp.trainable_distributions):由单个张量参数化的概率分布,使建立输出概率分布的神经网络变得容易。
第3层:概率推理
- 马尔可夫链Monte Carlo(tfp.mcmc):通过采样来近似积分的算法。包括Hamiltonian Monte
Carlo,随机游走Metropolis-Hastings,以及构建自定义过渡内核的能力。 - 变分推理(tfp.vi):通过优化来近似积分的算法。
- 优化器(tfp.optimizer):随机优化方法,扩展TensorFlow优化器,包括随机梯度Langevin动力学。
- 蒙特卡洛(tfp.monte_carlo):用于计算蒙特卡罗期望的工具。
第4层:预制模型和推理(类似于TensorFlow的预制估算器)
- 贝叶斯结构时间序列:用于拟合时间序列模型的高级接口(即类似于R的BSTS包)。
- 广义线性混合模型:用于拟合混合效应回归模型的高级界面(即与R的lme4软件包相似)。
TensorFlow Probability团队致力于通过尖端功能,持续更新代码和错误修复来支持用户和贡献者,我们将继续添加端到端的示例和教程。
让我们看看一些例子!
Edward2打造的线性混合效应模型
线性混合效应模型是对数据中结构化关系进行建模的简单方法,也可以称为分级线性模型,它分享各组数据点之间的统计强度,以便改进对任何单个数据点的推论。
作为演示,请考虑R中流行的lme4包中的InstEval数据集,其中包含大学课程及其评估评级。使用TensorFlow Probability,我们将模型指定为Edward2概率程序(tfp.edward2),它扩展了Edward。下面的程序根据其生成过程来确定模型:
import tensorflow as tf
from tensorflow_probability import edward2 as ed
def model(features):
# Set up fixed effects and other parameters.
intercept = tf.get_variable("intercept", [])
service_effects = tf.get_variable("service_effects", [])
student_stddev_unconstrained = tf.get_variable(
"student_stddev_pre", [])
instructor_stddev_unconstrained = tf.get_variable(
"instructor_stddev_pre", [])
# Set up random effects.
student_effects = ed.MultivariateNormalDiag(
loc=tf.zeros(num_students),
scale_identity_multiplier=tf.exp(
student_stddev_unconstrained),
name="student_effects")
instructor_effects = ed.MultivariateNormalDiag(
loc=tf.zeros(num_instructors),
scale_identity_multiplier=tf.exp(
instructor_stddev_unconstrained),
name="instructor_effects")
# Set up likelihood given fixed and random effects.
ratings = ed.Normal(
loc=(service_effects * features["service"] +
tf.gather(student_effects, features["students"]) +
tf.gather(instructor_effects, features["instructors"]) +
intercept),
scale=1.,
name="ratings")
return ratings该模型将“服务”“学生”和“教师”的特征字典作为输入,它们是每个元素描述单个课程的向量。该模型回归这些输入,假设潜在的随机变量,并返回课程评估评分的分布。在此输出上运行的TensorFlow会话将返回一代评级。
查看“线性混合效应模型”教程,详细了解如何使用tfp.mcmc.HamiltonianMonteCarlo算法训练模型,以及如何使用后预测来探索和解释模型。
高斯Copulas与TFP Bijectors
Copulas是一个多元概率分布,其中每个变量的边缘概率分布是均匀的。要构建使用TFP内在函数的copula,可以使用Bijectors和TransformedDistribution,这些抽象可以轻松创建复杂的分布,例如:
import tensorflow_probability as tfp
tfd = tfp.distributions
tfb = tfp.distributions.bijectors
# Example: Log-Normal Distribution
log_normal = tfd.TransformedDistribution(
distribution=tfd.Normal(loc=0., scale=1.),
bijector=tfb.Exp())
# Example: Kumaraswamy Distribution
Kumaraswamy = tfd.TransformedDistribution(
distribution=tfd.Uniform(low=0., high=1.),
bijector=tfb.Kumaraswamy(
concentration1=2.,
concentration0=2.))
# Example: Masked Autoregressive Flow
# https://arxiv.org/abs/1705.07057
shift_and_log_scale_fn = tfb.masked_autoregressive_default_template(
hidden_layers=[512, 512],
event_shape=[28*28])
maf = tfd.TransformedDistribution(
distribution=tfd.Normal(loc=0., scale=1.),
bijector=tfb.MaskedAutoregressiveFlow(
shift_and_log_scale_fn=shift_and_log_scale_fn))该“高斯系 Copula”创建了一些自定义Bijectors,然后展示了如何轻松地建立多个不同的Copula函数。有关分配的更多背景信息,请参阅“了解张量流量分布形状”。它介绍了如何管理抽样,批量训练和建模事件的形状。
带有TFP实用程序的变分自动编码器
变分自动编码器是一种机器学习模型,其使用一个学习系统来表示一些低维空间中的数据,并且使用第二学习系统来将低维表示还原为本来是输入的。由于TF支持自动分化,因此黑盒变换推理是一件轻而易举的事!例:
import tensorflow as tf
import tensorflow_probability as tfp
# Assumes user supplies `likelihood`, `prior`, `surrogate_posterior`
# functions and that each returns a
# tf.distribution.Distribution-like object.
elbo_loss = tfp.vi.monte_carlo_csiszar_f_divergence(
f=tfp.vi.kl_reverse, # Equivalent to "Evidence Lower BOund"
p_log_prob=lambda z: likelihood(z).log_prob(x) + prior().log_prob(z),
q=surrogate_posterior(x),
num_draws=1)
train = tf.train.AdamOptimizer(
learning_rate=0.01).minimize(elbo_loss)具有TFP概率层的贝叶斯神经网络
贝叶斯神经网络是一个神经网络,它的权重和偏差具有先验分布。它通过这些先验提供了改进的不确定性。贝叶斯神经网络也可以解释为神经网络的无限集合:分配给每个神经网络配置的概率是根据先前的。
作为一个小例子,我们使用了具有特征(形状为32 x 32 x 3的图像)和标签(值为0到9)的CIFAR-10数据集。为了拟合神经网络,我们将使用变分推理,这是一套方法来逼近神经网络在权重和偏差上的后验分布。也就是说,我们在TensorFlow Probabilistic Layers模块()中使用最近发布的Flipout估计器tfp.layers。
class MNISTModel(tf.keras.Model):
def __init__(self):
super(MNISTModel, self).__init__()
self.dense1 = tfp.layers.DenseFlipout(units=10)
self.dense2 = tfp.layers.DenseFlipout(units=10)
def call(self, input):
"""Run the model."""
result = self.dense1(input)
result = self.dense2(result)
# reuse variables from dense2 layer
result = self.dense2(result)
return result
model = MNISTModel()入门
要开始使用TensorFlow中的概率机器学习,请运行:
pip install --user --upgrade tfp-nightly
文章原标题《introducing-tensorflow-probability》
详情请阅读原文