初听说退火这个名词感觉就很(zhuang)帅(A__CDEFG...)
直到学了退火之后,我才发现:
退火不只是帅,而且非常万能
甚至比 D (大) F (法) S (师)还要万能
简直就是骗(de)分神器啊
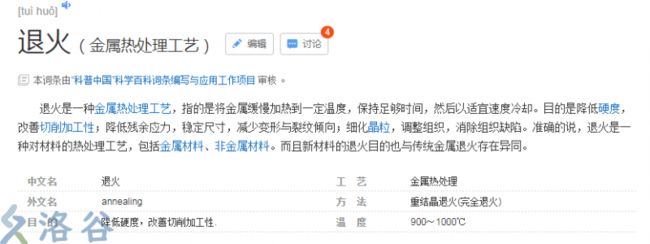
简介
作为一个计算机算法,它竟然在百度上有物理词条!
当时我看了就懵了,你说计算机一个算法,跟冶炼金属有什么关系啊?
后来我看了算法的词条...
是不是更懵了...
方便大家理解(变得更懵),我搬了百度上的定义:
Simulate Anneal Arithmetic (SAA,模拟退火算法)
根据Metropolis准则,粒子在温度T时趋于平衡的概率为e-ΔE/(kT),其中e为温度T时
的内能,ΔE为其改变量,k为Boltzmann常数。用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。
(懒的话不看也罢,本来就是拿来凑字数的)
说实话看完还是挺清楚(?)的,总计一下就是:
通过不断产生随机新解,并且比较新解与目前最优答案的差距大小;若新解较当今最有更优,就在新解的附近再产生下一个新解。通过大量的循环,从而达到引导答案最终趋向于标准最优解的目的。
稍微有点感觉了吧。
再说简单一点就是:
随便乱蒙答案,如果感觉蒙的比较好,就在它附近继续蒙
只要你蒙的足够多,你总能蒙到正确答案
...
(其实好像跟金属退火还没啥关系,没事 右上角洛谷日报2018: 浅谈玄学算法——退火 接着往下看)
->continue实现过程
既然是退火,那就得有火吧。
嗯...
对不起
这个还真没火(打开电脑主机,你会在你的CPU上看到火)
在计算机里面,退火过程主要用的是三个参数:初始温度T , 每次退火后温度变化量delta , 结束温度t 。其中a是一个略小于1的数。
说明一下这三个变量的用途吧,其实了解了用途之后应该也就能懂退火的原理了。
初始温度T:
这个主要决定的是我们随机蒙答案的范围。T越大,我们的随机答案就会分布地越广。主要保证的是算法的答案不会因为数据的偏移(过大或过小)而漏掉可能的正解。
只要是数据,T就一视同仁 。
结束温度t :
这个决定我们算法最后的精度。t越小,我们最后生成随机答案的范围就会越小。主要防止因为随机范围过大而造成的大量无意义的随机,能够保证我们最后的答案与标准答案相差无几(基本会被测试点无视或超出输出要求的精度),举个形象的栗子,我们t一般取的是1e-15(10的-15次方)。这里答案即使与标准答案有差,又有拿到题目会让你输出这种精度呢?
变化量delta(我不会打那个数学符号...):
T让我们随机的范围要广,t又说会把随机定到一个很小的范围。那到底随机随什么啊!
这个时候delta就出现了,它的作用就是在每次随机后让温度减小那么一点点(真的只是一点点)。让我们的随机从开始追求广度的T逐渐变化成强调细节的t。说白了就是让我们的退火既有T的广度,不会漏答案;又有t的精度。
看都这里可能又有人会懵了。你随机既要枚举广度,后面又要缩小范围。我咋知道所的范围是不是对的。没准你在错的答案附近随机蒙半天呢?
这个问题的答案其实就是退火算法的精髓:
对于随机的每一个答案:如果它比当前最优解更优,则接受它为当前最优解;若不是,则以一个跟当前温度有关的概率接受它。
->continue
理解
第一个人疑问可能所有看到这里的人都会问。
Q: 在随机时如果产生了一个并不是当前最优的新解,为什么不是直接开始下一轮的随机,而是以一个跟当前温度有关的概率接受它呢?
嗯...这个其实根本没法解释 挺好解释的。因为大家都知道,当前最优其实并不代表整体最优。因此我们在随机产生新解时,即使这个解是当前最优,我们仍然无法保证它会是整体最优。而我们每次枚举的范围是跟t相关的,所以其实开始并不是枚举所有可能的解;而是枚举一个范围超级大的解(在当前最优的基础上上下浮动一个关于t的函数)。而标准最优解可能与当前最优解位置或是数量相差较大。大到一次随机也无法达到那个范围。因此我们需要一些数作为中间过度。以让我们的随机能够随到整体最优解,而不会被 恶意卡数据的出题人陷害 当前最优蒙蔽了双眼。
所以是时候完整讲一下这个算法了;
通过随机rand函数,在当前的局部最优解上随机上下浮动(浮动幅度与当前温度成正相关)产生新解。对于每一个新解,若它较当前更优。则无条件接受它为当前最优解,否则则以一个概率(概率大小仍然与当前温度成正相关)来接受它。每一次随机结束后,将当前温度减小一点。
估计如果认真看了前面的人应该都 自闭 理解了。
它非常鲜明地体现了计算机的风格( 简单粗暴,以速度求质量 )
当然又有人要会问了。
Q: 既然在高温时接受当前不那么优的解的概率也趋近于1,也就是基本都接受了。那么凭什么最后能得到最优解呢?
其实我之前在学退火时也有这个问题。这个问题的答案其实就是退火算法之所以能得到最优解的理论依据。
因为如果出现更优解,我们是不考虑概率地无条件接受的;因此一个解越优,它被接受的总概率就会越大(虽然可能只会比次优解大0.00001%)。但是我们通过数百万次的随机运算不断地去扩大这个概率差(扩大是指数级增长的)。最终使得最优解的存活概率接近1。
这个随机到底随了多少次呢?
每一道题都有不同的次数,但大部分题的数量级是差不多的(程序时间就那么1000ms)。
就以P2210 Haywire例题来解答(其实我之前也不清楚)。我在我的代码里面加了一个countt变量,每一次随机运算它就自增一次,最后它的值有多大呢?
(17是答案,自己无视掉就行了)
足足有2357060!!!
值得一提的是我这题用的参数:
初始温度:3000
结束温度:1e -17( 10的负17次方 )
每次随机结束后温度的变化值:0.996( 温度 * 变化值 = 新温度 )
退火次数:20 ( 就前面三个参数重复调用了20次 )
其实也不必太吃惊,基本所有题目退火用的参数都是这几个( 可能次数会有点差异 )
->continue
例题
( 还是放例题讲容易点 )P1337 平衡点
作为一道纯正的几何物理题,竟然不给物竞的人做...
这题用模拟退火来做是考虑因为这题的最后解只有一个,况且比较好验证解(O n 复杂度还可以接受);并且如果用浮点运算的话可能会造成精度损失,最终影响答案。
#include
#include
#include
#include
#define cold 0.996 // 降温系数
#define temperature 3000 // 初始温度
#define time 4 // 退火次数( 这种纯物理题不用太多次 )
#define INF 999999
using namespace std ;
struct spot{
int x ;
int y ;
int weight ;
};
spot map[1001] ;
int n ;
double t ;
double tmpx , tmpy , tmpw ;
double ansx , ansy , anse ;
//double nowx , nowy , nowe ;
double energy ( double x , double y ){ // 判断当前点的能量,能量越小越稳定
double e = 0 ;
for( int i = 1 ; i <= n ; i ++ ){
tmpx = x -map[i].x ;
tmpy = y - map[i].y ;
tmpw = map[i].weight ;
e += sqrt( tmpx * tmpx + tmpy * tmpy ) * tmpw ;
}
return e ;
}
void colddown(){
t = temperature ;
while( t > 1e-15 ){ // 开始模拟退火
// cout << "debug" << " " << t << endl ;
double nowx = ansx + ( ( rand() * 2 ) - RAND_MAX ) * t ; // 随机产生一个值,使点位移
double nowy = ansy + ( ( rand() * 2 ) - RAND_MAX ) * t ;
double nowe = energy( nowx , nowy ) ;
double de = nowe - anse ;
// cout << nowx << " " << nowy << endl ;
if( de < 0 ){ // 如果当前解更优,就直接接受
ansx = nowx ;
ansy = nowy ;
anse = nowe ;
// cout << anse << endl ;
}
else{
if( exp( -de / t ) * RAND_MAX > rand() ){ // 否则以一个概率接受
ansx = nowx ;
ansy = nowy ;
}
}
t *= cold ;
}
}
void solve(){
for( int i = 1 ; i <= time ; i ++ ){
colddown() ; // 多来几次,保证结果正确性
}
}
int main () {
srand( 201821307 ) ; // 一个好的随机数种子很重要
cin >> n ;
for( int i = 1 ; i <= n ; i ++ ){
cin >> map[i].x >> map[i].y >> map[i].weight ;
ansx += map[i].x ;
ansy += map[i].y ;
}
ansx /= n ;
ansy /= n ;
anse = energy( ansx , ansy ) ;
solve() ;
printf( "%.3lf %.3lf" , ansx , ansy) ;
return 0 ;
} ( 注释掉的那几条是调程序时用的 )
其实这道题应该也不用多说,如果理解了前面的原理基本就不难懂。
( 竟然已经水了200多行 )
->continue
适用范围
虽然退火算法看起来好像非常暴力万能,但其实根dfs一样,也是有一定适用范围的。
答案较为简单,不许要输出过多数据的题目
能够在比较短的时间内验证答案( NP类问题都可以试试 )
不同的解之间有明显的互相转化的关系,及可以通过某个随机操作使一个解转化为另一个解
解集一半只有 1~3 个峰值,整体上呈现为数个单调函数
自己脸够白
非酋落下了WA的眼泪
最后要补充的一点是,可能你的算法并没有任何问题,但你题目就是A不了。其实这是退火算法造成的,毕竟是随机算法。如果退火的三个系数或是随机种子用的不够好。WA也是很正常的。
(比如这题我并没有改任何的代码,只是用不同的参数去退火,结果却能造成不同的分数 )
最后只能祝大家找的种子全部Ac 脱欧入非