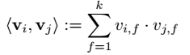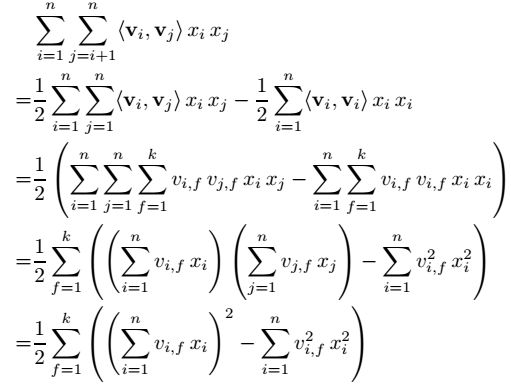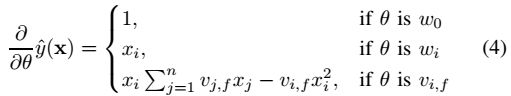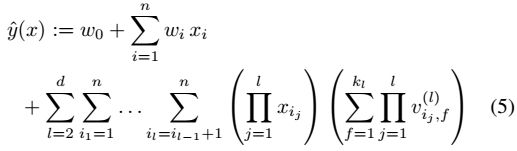摘要:在本文中,我们介绍了一种因式分解机,这是一种新的模型,结合了SVM的优点,利用了因式分解模型。类似SVM,因式分解机是一种通用的预测器,可以适用于任意的实值特征向量。对比SVM,FMs利用因式分解对变量之间的关系进行建模。因此,FMs可以在大量稀疏特征中进行相互关系的估计。我们展示了,模型的表达式可以在线性时间内求解,FMs可以进行直接的优化。所以,不像非线性的SVM,不需要进行对偶变换,模型的参数可以直接的进行估计,不需要用到支持向量。我们展示了和SVM的关系,以及在稀疏的设置下的参数估计的优势。
另外,有许多因式分解模型如矩阵分解,并行因子分析如SVD++,PITF,FPMC。这些方法的缺点是通用性不好,只对特殊的输入数据有用。优化方法对于不同的任务也各不相同。我们展示了,FMs通过制定不同的输入就可以模拟这些模型。这就使得FMs非常的易用,甚至可以不需要因式分解分解模型的专业知识都可以。
1、介绍
SVM是机器学习和数据挖掘中最流行的算法之一。然而在协同过滤的场景中,SVM并不重要,最好的模型要么直接使用矩阵的因式分解或者使用因式分解参数。本文中,我们会展示,SVM之所以在这些任务中表现不好,是因为SVM在复杂的非线性的稀疏的核空间中很难找到一个好的分割超平面。而张量分解模型的缺点在于(1)不用应用于标准的预测数据(2)不同的任务需要特殊的模型设计和学习算法。
本文中,我们介绍了一个新的预测器,Factorization Machine(FM),是一个像SVM一样的通用的预测模型,但是可以在非常稀疏的数据中估计出可靠的参数。FM对所有变量的相互关系的进行建模(对比SVM的多项式核),但是利用了可因式分解的参数,而不是像SVM一样使用了稠密的参数。我们展示了,模型的表达式可以在线性时间内求解,而且只依赖与线性数量大小的参数。这就允许了直接进行优化和存储模型的参数,而不需要存储任何的训练数据。(SVM是需要存储支持向量的)。非线性的SVM通常使用对偶形式进行求解,而且会使用到支持向量。我们也显示了在协同过滤的业务上FMs比许多很成功的模型如带偏置的MF,SVD++,PITF,FPMC等都好。
总的来说,FM的优点:
1)FMs可以在非常稀疏的数据上进行参数估计。
2)FMs的复杂度是线性的,方便优化,不需要依赖支持向量,适用于大型的数据集。
3)FMs是通用的预测模型,可以适用于任意的实值的特征向量。
2、在稀疏数据下进行预测
大部分的常用的预测任务是估计一个预测的函数,从一个实数向量到目标T(如果是回归任务T=R,如果是分类任务T={+,-})。在监督学习中,假设有个数据集,我们也研究了排序的任务,函数y可以用对x向量的评分。评分函数可以通过成对的数据进行训练。由于成对数据是反对称的,可以直接使用正的实例。
在本文中,我们要解决的问题是数据的稀疏问题,也就是说在x向量中,大部分的值都是0,只有少部分不是0。稀疏的特征在现实世界中是非常常见的,如文本分析和推荐系统中。
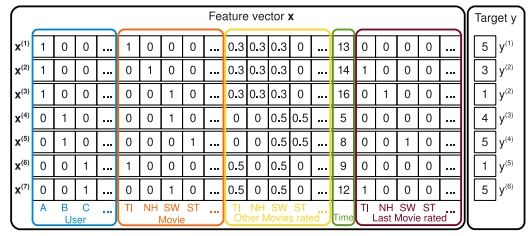
例1 假设我们有个电影评分系统,系统记录了用户在特定的时间对电影的评分{1,2,3,4,5},用户U和电影I为:
观察到的数据S为:
任务是使用这些数据,预测一个函数y,预测一个用户在某个时间对某个电影的评分。
图1显示了创建的特征向量,每一行是一个样本,包括了特征向量x和对应的评分y,前4列表示了用户的属性,后面5列表示了当前评价的是哪个电影,再后面表示了用户评价过的其他的电影的分数,这些分数做过归一化,再后面是时间,从2009年1月开始计算,用月数来表示,比如16就是从2009年1月开始往后数16个月,就是2010年4月;最后几列表示用户评价过的最后一个电影,最右边的是当前电影的评分y。
在本文中,我们将使用整个数据集来进行演示。
3、因式分解机(FM)
A. 因式分解模型
1)模型方程:2阶的模型方程:
其中,<·,·>表示长度为k的点乘,k是一个超参数:
2阶的FM能过获取所有的单个特征和配对特征的相互关系。第i和第j个变量的相互关系并没有直接使用wij来表示,而是通过因子v的方式来表达,这就是最关键的地方,这种方法使得我们在更高阶的稀疏数据上也可以进行很好的参数估计。
2)表达能力:我们知道对于正定矩阵W,存在矩阵V,使得W=V·V’,k足够大。然而对于稀疏的情况,应该选择一个比较小的k,因为没有足够的数据去预测一个复杂的W。限制k,也就是FM的表达能力,能够提高稀疏情况下的相互关系矩阵的泛化性能。
3)稀疏情况下的参数估计:在稀疏情况下,通常没有足够的数据进行直接的参数估计。因式分解机可以进行稀疏的估计,是因为进行了因式分解之后,用来估计一个参数的数据也可以用来估计相关的另一个参数。比如说,我想预测两个用户之间的相互关系参数,来预测y,从图1可以看到,在每个样本中,用户的向量是one-hot,也就是说,在一个样本中,两个用户的参数不会都是非0数,如果直接进行估计的话,那么A和B的相互关系参数会估计成0。但是如果进行因式分解机的预测话,就不会这样了。
4)计算量:接下来,我们展示如何让FMs变得实际可用。方程(1)的计算复杂度是O(kn2),但是通过下面的变换,会变成线性的时间复杂度O(kn)。在稀疏的情况下,大部分的x中的元素都是0,我们在计算的时候,只需要进行非0值的计算就可以了。
B. 使用因式分解机进行预测
因式分解机可以用在各种预测任务中:
l 回归:直接进行预测,使用最小均方误差进行优化。
l 二分类:使用合页损失或者对数几率损失进行优化。
l 排序:对预测的分数进行排序,可以通过成对实例的分类损失进行优化。
在上面所有的情况下,都可以使用L2的正则化来防止过拟合。
C. 因式分解机的学习
FMs的参数可以通过梯度下降的方式来求解:
其中,是和i无关的,可以事先求出来。每个梯度都可以在O(1)时间内求得,整体的参数更新的时间为O(kn)。
我们提供了一个通用的实现,LIBFM(http://www.libfm.org),使用SGD,支持元素和配对的loss。
D. d阶的因式分解机
2阶的因式分解机可以很容易的推广到d阶
其中,第l个相互关系参数可以通过PARAFAC模型进行因式分解。通过变换,同样可以在线性的时间复杂度上求解。
E. 总结
FMs的优点:
1)可以在稀疏的情况下进行很好的参数估计,特别是可以估计没有观测到的相互关系。
2)参数的大小和运算时间都是线性的,可以通过SGD进行参数的更新,可以使用多种loss。
4、FMs vs. SVMs
A. SVM模型
我们看一下SVM模型和FMs的关系,我们知道SVM可以表示成变换后的特征向量和
参数的内积的形式,这个参数的变换我们通常使用核函数来进行。
1)线性核:和FM为1阶的情况完全等效
2)多项式核:当多项式为2阶的时候,SVM对所有的相互关系使用了独立的参数,而FMs则通过因子的方式来共享相互关系之间的参数。
B. 稀疏情况下的参数估计
我们下面解释一下为什么SVM在稀疏的情况下表现不好。
1)线性SVM:在这种情况下线性SVM对应到了一个非常简单的模型,因为只有少数的几个参数。所以模型的参数的预测在这种稀疏情况下也会不错,但是预测的质量却不好,见图2。
2)多项式SVM:这种情况下,SVM可以获取高阶的相互关系,但由于是x是稀疏的,所以最后的模型也是非常简单的模型,所以,结果也不会比线性的SVM更好。
C. 总结
1)SVM的稠密的参数需要相互关系的直接的观测值,而在稀疏的输入的情况下,这种直接的观测值很少。
2)FMs可以直接进行学习,非线性的SVM通常在对偶形式进行求解。
3)FMs的函数不依赖与训练数据SVM的预测依赖部分训练数据(支持向量)。
5、FMs vs. 其他的因式分解模型
FMs可以通过使用合适的输入来模拟很多其他的因式分解模型。
6、结论
本文介绍了因式分解机(FMs)。并对和SVM进行了对比,以及和其他的因式分解模型进行了对比。FMs对于解决稀疏的输入相比SVM能够有很好的效果,参数和复杂度都是线性的,而且可以直接用SGD进行优化。FMs可以适用于任意的实值的预测。
本文可以任意转载,转载时请注明作者及原文地址。