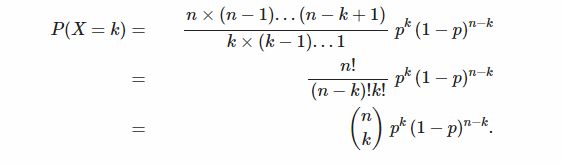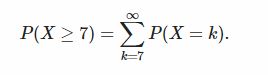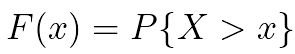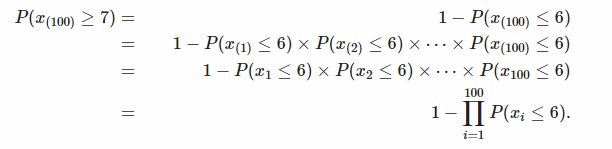《Modern Statistics for Modern Biology》Chapter 一：离散数据模型的预测（1.1

Modern Statistics for Modern Biology

书籍目录

在分子生物学中，许多情况涉及计数事件：有多少密码子使用某种拼写，有多少DNA的reads比对到参考序列上，DNA序列中CG的含量。这些计数为我们提供了离散的变量，而不是像质量和强度这样的量是在连续的尺度上测量的。
如果我们知道所研究的机制所遵循的规则，即使结果是随机的，我们也可以通过计算和标准的概率定律来生成我们感兴趣的任何事件的概率。这是一种自上而下的方法，基于演绎和我们对如何操纵概率的知识。在第2章中，您将看到如何将其与数据驱动(自底向上)统计建模相结合。

1.1 本章的目标

了解如何从给定的模型中获得所有可能结果的概率，并了解如何将理论频率与在实际数据中观察到的频率进行比较。
探索一个完整的例子，如何使用泊松分布分析数据的表位检测。
如何对试验离散数据生成最有效的模型：泊松、二项和多项分布。
使用R中相关函数计算概率和计数罕见事件。
通过指定的分布生成随机数。

1.2 一个真实的案例

涉及markdown语法参考链接：

CSDN-markdown语法之如何使用LaTeX语法编写数学公式
Markdown中公式的写法(Latex)
　　　　　　　　　　　　　　　　　　 $\sqrt{x^3}$ :

我们被告知人类免疫缺陷病毒(HIV)基因组上的突变是随机发生的，每个复制周期的核苷酸数为5×10⁻⁴。这意味着，在一个周期之后，大约10⁴=10 000个核苷酸的基因组中的突变数量将遵循泊松分布,我们将在稍后给出更多关于这种概率分布的详细信息。利率为5。这说明了什么？这个概率模型预测，在一个复制周期中的突变数量将接近5个，并且这个估计的可变性是(标准误差)。我们现在已经有了我们期望在一个典型的HIV毒株中看到的突变数量及其变异性的基线参考值。

事实上，我们可以推断出更详细的信息。如果我们想知道在Poisson(5)模型下发生3个突变的频率，我们可以使用一个R函数来生成看到x=3个事件的概率，取泊松分布的发生率参数的值，称为lambda(λ希腊字母，例如λ和μ通常表示表征我们使用的概率分布的重要参数)。 X表示给定区间的事件发生次数，例如一个星期内的损坏次数。如果X符合泊松分布，且每个区间内平均发生的λ次，或者说发生率为λ，则写作：X ~ Po(λ)

> dpois(x = 3, lambda = 5)
[1] 0.1403739

这就是说，看到三个事件的几率大约是0.14，也就是大约7个事件中就有1个。

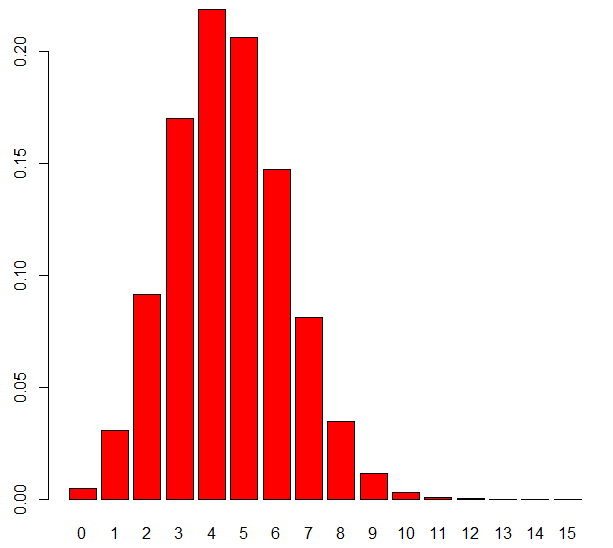
如果要生成从0到12的所有值的概率，则不需要编写循环。我们可以简单地将第一个参数设置为这13个值的向量，使用R的序列操作符，冒号":"。我们可以通过绘制它们来查看概率(图1.1)。

> 0:12
 [1]  0  1  2  3  4  5  6  7  8  9 10 11 12
> dpois(x = 0:12, lambda = 5)
 [1] 0.006737947 0.033689735 0.084224337 0.140373896 0.175467370 0.175467370
 [7] 0.146222808 0.104444863 0.065278039 0.036265577 0.018132789 0.008242177
[13] 0.003434240
> test <- dpois(x = 0:12, lambda = 5)
> barplot(test, names.arg = 0:12, col = "red")    ## 图1.1

names.arg:  在每个条下出现的名称的向量

《Modern Statistics for Modern Biology》Chapter 一：离散数据模型的预测（1.1 - 1.3）_第2张图片

图1.1

数学理论告诉我们，看到值 x的泊松概率是由公式

给出的。在这本书中，我们将不时地讨论理论，但更倾向于显示具体的数值例子和可视化，如图 1.1。

1.3 使用离散概率模型

点突变可以发生也可以不发生；它是一个二进制事件。两种可能的结果(是, 否)称为范畴变量的级别。

并非所有事件都是二进制的。例如，一个二倍体生物的基因型可以分为三个水平(AA, Aa, aa)。

有时，一个分类变量中的水平数非常大；例如，生物样本中不同类型的细菌的数量(数百或数千)和由3个核苷酸(64种)组成的密码子的数量。

当我们在一个样本上测量一个分类变量时，我们经常想要统计一个计数矢量中不同级别的频率。R对范畴变量有一种特殊的编码，并将其称为factor。在这里，我们抽取了不同的血液基因型的19名受试者绘总成一个表。

> genotype =  c("AA","AO","BB","AO","OO","AO","AA","BO","BO",
+              "AO","BB","AO","BO","AB","OO","AB","BB","AO","AO")
> table(genotype)
genotype
AA AB AO BB BO OO 
 2  2  7  3  3  2

在创建factor时，R会自动检测。可以使用R中“levels”函数功能查看level。

> genotypeF = factor(genotype)
> levels(genotypeF)
[1] "AA" "AB" "AO" "BB" "BO" "OO"
> table(genotypeF)
genotypeF
AA AB AO BB BO OO 
 2  2  7  3  3  2

► 问题1.1：如果您想要创建一个尚未在数据中包含某些level的factor，该怎么办？
factor(genotypeF, levels = c("AA", "AB", "AO", "BB", "BO", "OO", "new_levels"))

1.3.1 伯努利试验

最为经典的是抛硬币实验，抛开外在因素的干扰，投掷一枚硬币，落地后的结果只有两个：正面和反面。这是一个简单的伯努利试验，输出的结果所谓的伯努利随机变量。R语言中binom用来做伯努利试验计算。
假设我们要模拟15次投掷硬币的结果，将概率设置为0.5得到15次的结果。

> rbinom(15, prob = 0.5, size = 1)
 [1] 0 1 0 1 0 0 1 0 1 0 0 1 0 0 1

我们将rbinom函数与一组特定的参数66一起用于R函数，参数也称为参数：第一个参数是我们要观察的试验次数；在这里我们选择了15个。我们通过prob参数来指定成功的可能性。按size=1（表示只有两个结果0或者1），每个单独的判断只包括一次掷硬币。

► 问题1.2：重复此函数调用多次。为什么答案不总是一样的？
因为这是一个随机分布函数，随着重复的次数越来越多，最终的比例越接近刚开始指定的prob.

在伯努利试验中成功和失败可以为不相等的概率事件，只要概率和为1就行。为了模拟12次把球扔进两个盒子的试验，如图1.2所示，在如下右边的盒子和左边的盒子中

《Modern Statistics for Modern Biology》Chapter 一：离散数据模型的预测（1.1 - 1.3）_第3张图片

图 1.2

> rbinom(15, prob = 0.5, size = 1)
 [1] 1 0 1 0 0 0 0 1 0 1 1 0 1 0 1

1表示成功，表示这个球落入到右边的箱子中；0表示落入到左边的箱子中。

1.3.2 Binomial success counts （翻译不准，故放原文）

如果我们只关心有多少个球落入到右边的箱子中，而不关心它们落入的顺序，我们只需就落入到右边的箱子中的1加起来求和即可。因此而不是上面看到的向量: vector，我们只需要单一的一个数字结果。在R中只需将rbinom函数的size参数设置为12即可。

> rbinom(1, prob = 2/3, size = 12)
[1] 9

这个结果告诉当我们将概率设置为时候有多少个球会落到右边的箱子中。当我们输出结果只有两种可能时，我们可以使用随机的two-box模型，比如：头或者尾、成功或者失败、CpG或者non-CpG(甲基化或者未甲基化)、M或者F（男性还是女性）、Y = 嘧啶或者R= 嘌呤、患病的或者健康的、正确或者错误。我们只需要计算成功的可能性p，自然而然就得到了失败的可能性1 - p。 SSSSSFSSSSFFFSF 总结为 (#Successes=10, #Failures=5), 或者看做x = 10, n = 15
在15次伯努利试验中，当成功的概率为0.3时结果为成功的次数就称为一个二项式随机变量或者一个服从B(15, 0.3)分布的随机变量。下面在R中使用函数rbinom将试验次数设置为15：

> set.seed(235569515) ## 上面不是提到不同人运行结果不一样，这里设置seed后大家运行的结果就一致了。
> rbinom(1, prob = 0.3, size = 15)
[1] 5

► 问题 1.3 ：将此函数调用重复十次。最常见的结果是什么？
4，因为毕竟这是一个服从B(15, 0.3)的二项分布函数

The complete probability mass distribution is available by typing:

> probabilities = dbinom(0:15, prob = 0.3, size = 15)
> round(probabilities, 2)
 [1] 0.00 0.03 0.09 0.17 0.22 0.21 0.15 0.08 0.03 0.01 0.00 0.00 0.00 0.00 0.00 0.00

绘制上面数据的分布图

barplot(probabilities, names.arg = 0:15, col = "red")

《Modern Statistics for Modern Biology》Chapter 一：离散数据模型的预测（1.1 - 1.3）_第4张图片

图 1.3 可以看到频率最高的为4

我们通常在R中通过指定size 参数来确定试验的次数，并且经常用n表示，成功的概率用p表示。使用数学术语来将X是服从参数(n, p)的二项分布写作 X ~ B(n, p), X成功的概率为：

► 问题 1.4 当k = 3, p = , n = 4时，结果为什么？

> dbinom(3, prob = 2/3, size = 4)
[1] 0.3950617

小插曲: R计算二项Binomial分布的P
pbinom(q,size,prob): 计算累积概率
dbinom(x,size,prob): 计算取某个值的特定概率
rbinom(n, size, prob): 产生n个b(size,prob)的二项分布随机数
qbinom(p, size, prob): quantile function 分位数函数。

#x 
     vector of (non-negative integer) quantiles.
     分位数（非负整数）向量。
#q 
     vector of quantiles.
     分位数向量。
#p 
     vector of probabilities.
     概率向量。
#n 
     number of random values to return.
     返回随机值的数量。
#lambda 
     vector of (non-negative) means.

     均值（非负）向量。

#log, log.p 
     logical; if TRUE, probabilities p are given as log(p).
     逻辑型，如果为真，概率p作为log(p)给定。

#lower.tail 
     logical; if TRUE (default), probabilities are P[X ≤ x], otherwise, P[X > x].
     逻辑型，如果为真（默认），概率是P[X<=x], 否则概率为P[X>x].

假定在一次实验中，事件A发生的概率为0.1，那么进行11次这样的实验，观察到4次的概率是多少？
答案是Binomial Probability: P(X = 4)= dbinom(4,11,0.1)
[1] 0.0157838

观察到小于等于4次的概率是多少？
Cumulative Probability: P(X < =4)= pbinom(4,11,0.1)
[1] 0.997249

1.3.3 泊松分布

当我们的试验次数n很大切成功的概率p很小的时候, 二项分布B(n, p)可以完全近似的认为是一个更简单λ = np的泊松分布，在图 1.1 的HIV试验中涉及。
► 问题 1.5
当每个碱基突变的概率为p = 5 * 10^-4 时候，基因组上n=10⁴个碱基观察到0:12个突变的分布是什么? 当用二项分布B(n, p)和泊松分布（λ = np）为模型时，结果是否相似？
请注意，与二项分布不同，泊松分布不再依赖于两个独立的参数n和p，而只依赖于它们的乘积np。在二项分布的情况下，我们也有一个计算泊松概率的数学公式。
　　　　　　　　　　　　　　　　
例如：将 λ = 5代入，计算P(X = 3)

> 5^3 * exp(-5) / factorial(3)
[1] 0.1403739

> dpois(3, 5)
[1] 0.1403739

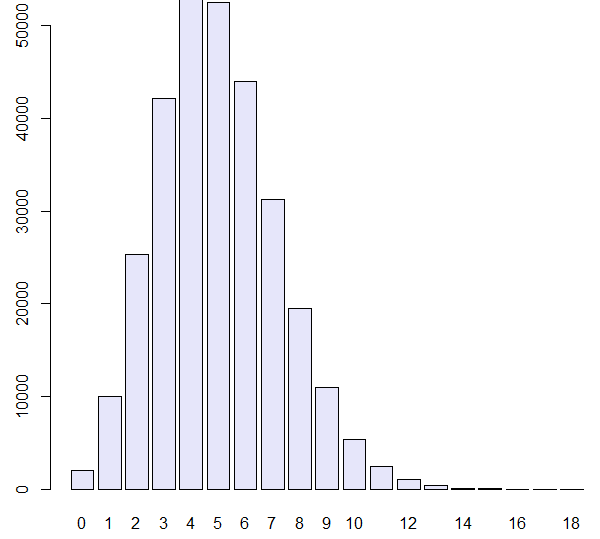
可以使用dpois(x, λ)来计算。
同样的上面碱基突变问题，模拟10000个位点的突变过程，突变率为5×10^-4，并计算突变数。多次重复此操作，并使用barlot函数绘制分布。

> rbinom(1, prob = 5e-4, size = 10000)
[1] 2
> simulations = rbinom(n = 300000, prob = 5e-4, size = 10000)
> barplot(table(simulations), col = "lavender")

《Modern Statistics for Modern Biology》Chapter 一：离散数据模型的预测（1.1 - 1.3）_第6张图片

1.3.4 A generative model for epitope detection

在测试某些药物化合物时，检测引起过敏反应的蛋白质是很重要的。负责这些反应的分子位点被称为表位。表位的技术定义是：
　　抗体与大分子抗原结合的特定部分。对于T细胞识别的蛋白质抗原，表位或决定簇是与主要组织相容性复合物(MHC)分子结合以供T细胞受体(TCR)识别的肽段或位点。
如果你对免疫学不是很熟悉的话：抗体(如图1.6所示)是由某些白细胞产生的一种蛋白质，对身体中的一种外来物质作出反应，这就是所谓的抗原。

　　

抗体图，显示几种颜色的免疫球蛋白结构域
抗体与其抗原结合(或多或少具有特异性)。结合的目的是帮助破坏抗原。抗体可以通过几种方式发挥作用，取决于抗原的性质。有些抗体直接破坏抗原。其他人帮助招募白血球来破坏抗原。抗原表位，也称为抗原决定簇，是被免疫系统识别的抗原的一部分，特别是被抗体、B细胞或T细胞识别。

已知参数的`ELISA`误差模型

ELISA酶联免疫吸附试验。检测方法用于检测蛋白质不同位置的特定表位。假设我们使用的ELISA阵列具有以下事实：

每个位置的基线噪声水平，或者更准确地说，假阳性率为1%。这是表示一个成功的可能性-当没有的时候我们认为我们有一个表位。我们写这个P( declare epitope |no epitope)
这种蛋白质是在100个不同的位置测试的，应该是独立的。
我们将对50个病人样本进行检查。

一个病人的数据

一个病人的芯片数据如下

##   [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
##  [30] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [59] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
##  [88] 0 0 0 0 0 0 0 0 0 0 0 0 0

其中，1表示击中(因此可能发生过敏反应)，0表示在该位置没有反应。
通过仿真验证了p = 0.01的50个独立伯努利变量之和与Poission(0.5)随机变量相同，具有足够好的逼近性。

50个芯片数据的结果

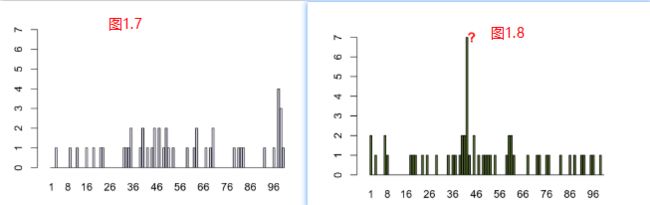
我们将研究所有50名患者在100个位置上的数据。如果没有过敏反应，假阳性率意味着对于一个病人来说，每一个位置都有1/100的概率是1。因此，在对50名患者进行统计后，我们期望在任何给定的位置，50个观察到的(0，1)个变量之和有一个参数为0.5的泊松分布。典型的结果可能如图1.7所示。现在假设我们看到了如图1.8所示的实际数据，它作为R对象e100从数据文件e100.RData加载。

> setwd(dir = "E://compute language/NGS/Modern Statistics for Modern Biology/data")
> load("e100.RData")
> barplot(e100, ylim = c(0, 7), width = 0.7, xlim = c(-0.5, 100.5),
+   names.arg = seq(along = e100), col = "darkolivegreen")

《Modern Statistics for Modern Biology》Chapter 一：离散数据模型的预测（1.1 - 1.3）_第8张图片

图1.8中的峰值是惊人的。如果没有表位，那么看到7这样大的值的可能性有多大？如果我们考虑一个泊松(0.5)随机变量时，看到一个7(或更大)的数字的概率，那么答案可以用如下的封闭形式来计算:
这当然与1−P(X≤6)相同。概率P(X≤6)是6的所谓累积分布函数，R有用来计算它的函数ppois，我们可以用以下两种方法中的任何一种来使用它：

> 1 - ppois(6, 0.5)
[1] 1.00238e-06

> ppois(6, 0.5, lower.tail = FALSE)
[1] 1.00238e-06

小插曲： ppois是泊松分布的分布函数（即用来求累计概率），因为是离散的，所以只会在整数左右有变化, R语言中ppois如何应用
ppois(q, lambda, lower.tail = TRUE, log.p = FALSE)
q：官方帮助文档说是分位数，指定x轴上的点。
lambda：就是泊松分布的参数λ
lower.tail：是逻辑变量，当它为真(TRUE，缺省值)时，分布函数的计算公式为

当lower.tail = FALSE时，分布函数的计算公式为

log,log.p是逻辑变量，当它为真(TRUE)时，函数的返回值不再是泊松分布，而是对数泊松分布.
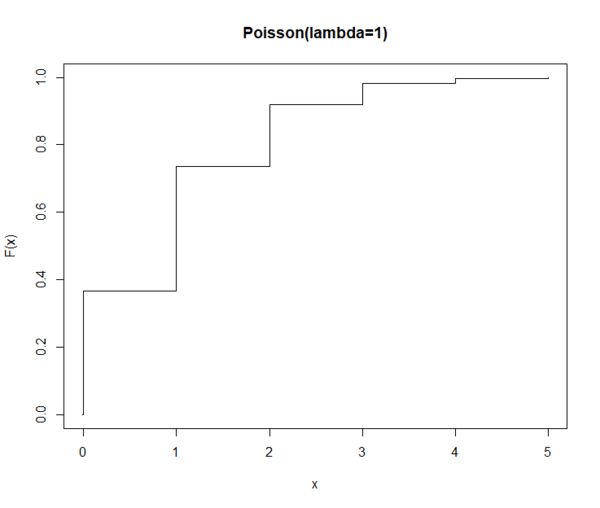
比如lambda=1的分布函数作图如下：
在假设没有表位反应的情况下，看到7的概率是：

Poisson分布的极值分析

停，停止!。在这种情况下，上述计算不是正确的计算。

► 问题1.6
如果我们想要计算在没有表位的情况下观察到这些数据的概率，你能发现我们推理中的缺陷吗？

因此，我们不应该问，看到泊松(0.5)大到7的概率有多大，而应该问自己，100泊松(0.5)试验的最大值达到7的可能性有多大？我们在这里使用极值分析，这意味着我们对随机分布的非常大或非常小的值的行为感兴趣，例如，最大值或最小值。我们对数据值x₁、x₂，x₃,...,x₁₀₀进行排序，并且重新命名为x₍₁₎、x₍₂₎，x₍₃₎,...,x₍₁₀₀₎, 使得x₍₁₎表示100个树中上最小值，x₍₁₀₀₎表示最大值。x₍₁₎...x₍₁₀₀₎称为这个样本的100个值的秩统计量。
最大值为7是所有100个计数都小于或等于6的互补事件。两个互补事件的概率之和为1。因为位置应该是独立的，所以我们现在可以进行计算了。
因为我们假设这100个事件中的每个事件都是独立的，所以我们可以使用上面的结果。

真实的计算数字

我们可以让R计算这个数字的值：(1−ϵ)¹⁰⁰。对于那些对这些计算如何通过近似值快捷的感兴趣的人，我们给出了一些细节。这些可以在第一次阅读时跳过。
我们从上面回忆起，ϵ ≃ 10⁻⁶比1小得多。为了近似计算(1−ϵ)¹⁰⁰的值，我们可以使用二项式定理，去掉ϵ的所有“高阶”项，即ϵ²，ϵ³,...的所有项, 因为与其余的(“领先”)术语相比，它们小得可以忽略不计。
另一个等价的路由是使用近似的e^−ϵ ≃ 1−ϵ，与log(1−ϵ)≃−ϵ一样。因此
因此，如果没有表位，在100个位置中看到一些大小或大于7的点击的正确概率大约是我们以前错误计算的概率的100倍。
10⁻⁶和10⁻⁴的计算概率均小于标准显著性阈值(0.05、0.01或0.001)。拒绝任何表位无效的决定也是一样的。然而，如果一个人必须在法庭上站起来，像在一些法庭案件中那样，将p值辩护到8个有效数字(1717年，这发生在OJ Simpson案的法医证据审查中)。那就是另一回事了。考虑到测试多重性的调整后的p值是应该报告的值，我们将在第6章中回到这一重要问题。

模拟计算概率

在我们刚才看到的情况下，理论上的概率计算是相当简单的，我们可以通过一个明确的计算来计算结果。在实践中，事情往往更复杂，我们更好地计算我们的概率使用蒙特卡洛方法：一种基于我们的生成模型的计算机模拟，找到我们感兴趣的事件的概率。下面，我们将生成100000个从100个泊松分布数中选取最大值的实例。

> maxes = replicate(100000, {
+   max(rpois(100, 0.5))
+ })
> table(maxes)
maxes
    1     2     3     4     5     6     7     9 
    7 23059 60817 14355  1605   141    15     1

在100000个试验中，有16个试验的最大值在7个或7以上。这给出了P(X_max ≥ 7)的以下近似值：

> mean( maxes >= 7 )
[1] 0.00016

这与我们的理论计算基本一致。我们已经看到蒙特卡罗模拟的一个潜在限制：模拟结果的“粒度”由模拟次数(100000)的倒数决定，因此将大约为。任何估计的概率都不能比这个粒度更精确，事实上，我们估计的精度将是这个粒度的几倍。到目前为止，我们所做的一切都是可能的，因为我们知道每个位置的假阳性率，我们知道被检测的病人人数和蛋白质的长度，我们假设我们从模型中得出了相同分布的独立图，我们假设我们有来自模型的同分布的独立画法，并且没有未知的参数。这是一个概率或生成建模的例子：所有的参数都是已知的，数学理论允许我们以一种自上而下的方式进行推理。
相反，如果我们在更现实的情况下知道病人的数量和蛋白质的长度，但不知道数据的分布，那么我们就必须使用统计模型。这一方法将在第2章中阐述。我们将看到，如果我们只有数据开始，我们首先需要适合一个合理的分布来描述它。然而，在我们讨论这个更困难的问题之前，让我们将离散分布的知识扩展到不仅仅是二进制的、成功或失败的结果。

《Modern Statistics for Modern Biology》Chapter 一： 离散数据模型的预测（1.1 - 1.3）