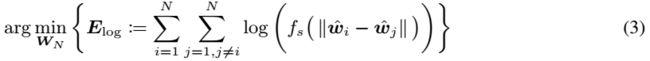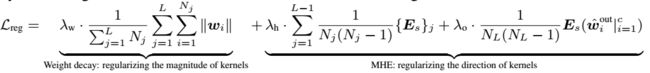摘要:神经网络是一种强大的非线性函数,可以在很多应用上进行端到端的训练。同时,过度的参数化的本性使得它可以拟合非常复杂的函数,具有非常强大的表达能力,可以解决非常困难的任务,也会导致出现高度相关性的神经元,会伤害到模型的泛化能力,并导致不必要的计算的损耗。因此,如何对网络进行正则化,避免冗余的表达能力,就成为了非常重要的问题。为了这个目的,我们从一个非常有名的物理问题中得到启发—Thomson problem,找到这样一个状态,让在单位球体上的N个电子,尽可能的均匀分布,这样具有最小的势能。根据这种直觉,我们减小了冗余的正则化,泛化了能量最小的问题。提出了最小化超球面能(MHE)量的目标作为神经网络的通用的正则化。我们也提出了一些新的MHE的变体,提供了一些来自理论观点的直觉。最后,我们将MHE正则化用在了几个具有挑战性的项目上,并通过实验显示了这些直觉的有效性,并显示了使用了MHE正则化的卓越表现。
1 介绍
最近,深度学习在很多任务上取得了很大的成功。利用过度参数化的本质,深度学习网络和深度结构,在很多的大规模数据的问题上得到了非常好的性能。但是,除了这些成功之处,由于过度参数化而导致的具有冗余和高度相关的神经元(比如卷积中滤波器的权重),也成为了一个问题。这也激发了一系列相关的工作,如网络的压缩,更加高效的网络结构。这些工作要么是对网络进行剪枝,要么重新设计一个网络结构,目的是在减少参数的基础上保持尽可能高的性能。目前,找一个统一的理论和原则来指导网络进行压缩来提高模型的泛化能力,仍然是一个开放性的问题。
另一方面,一部分工作试图通过多样性的分析来缓解冗余,达到提高泛化能力的作用。大多数的工作通过正则化强行得到大的多样性。我们的工作也是属于这一类,共享相似的高层的目标,但是背后的直觉却不一样。特别的,最近的趋势在loss和卷积层面是学习特征之间的角度信息。其中,关键的直觉在于,角度保留了最丰富的可分性的信息。结果,很自然的,神经元之间的几何超球面距离成为了其中的关键。直觉就是通过让特征在单位球体上的投影相互远离彼此,来得到特征的可分性。同时,还有一些工作也考虑到了角度的可分析,但是没有考虑到整体的分布,所以没有取得state of the art。
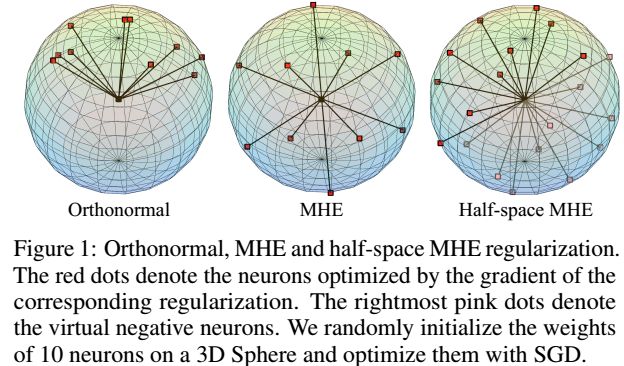
有了上面的动机,我们从一个著名的物理问题中得到启发,叫做Thomson问题,Thomson问题的目的是在一个单位球体上,使得N个电子的分布具有最小的势能。我们找到Thomson问题和我们的问题的本质,多样性的神经元的问题可以看做是找到一个最优的电子位置的配置。类似的,我们将神经元的多样性通过成对的相互关系,表示为超球面上的势能。高势能表示高的冗余性,低势能表示这些神经元具有更加丰富的多样性,在空间中更加的一致。为了减少神经元的势能,提升网络的能力,我们提出了一个新的minimum hyperspherical energy (MHE)正则化框架,其中,通过减少每一层的神经元的势能,来提升神经元的多样性。通过很多的实验的验证,MHE确实可以提升模型的泛化能力。MHE用在隐藏层和输出层的时候,需要面对不同的情况。对于隐藏层,直接使用MHE仍然可能导致某种程度上的冗余,因为会产生指向相反方向的点。为了避免这种多样性,我们提出了半空间的MHE,构建一组虚拟的神经元,然后对于所有的真实和虚拟的神经元,最小化超球面的势能。对于输出层,MHE的目的是将分类神经元尽可能均匀的分布,来提升类间特征的可分性。和隐藏层的MHE不同,分类神经元应该分布在整个超球面上,来得到最佳的分类性能。和广泛使用的正交正则化进行一个直觉性的比较,MHE和半球面的MHE如下图。你可以发现,MHE和半球面MHE都将神经元均匀的分布在超球面或者半超球面上。相比之下,卷积的正交正则化趋向于将神经元靠的更近,特别是当神经元的数量远大于维度的时候。
MHE的原始定义是基于欧式距离的,然而,我们进一步考虑使用角度距离来最小化能量,后面我们把这个叫做A-MHE。另外,我们加了一些理论的见解,讨论的逐渐逼近的表现和泛化误差。最后,我们将MHE用到了几个不同的任务上,包括通用的目标检测,类别不均衡的学习,还有人脸识别。在实验中,我们展示了MHE对于结构不敏感,可以用来提高泛化的性能。
2 相关的工作
多样性的正则化在稀疏编码,集成学习,self-paced learning ,度量学习中是有用的,在稀疏编码的早期的研究中表明,可以通过多样性正则化来提升密码本的泛化能力,这里,多样性往往使用协方差矩阵来表示。最近一段时间,有一系列的工作研究了神经网络中的多样性正则化,这里,多样性通过大的角度/正交性,或者减小基之间的协方差来得到。我们的工作和这些都不一样,我们在整个超球面上考虑神经元的多样性,通过一个更加全局的,自顶向下的角度来考虑多样性。
多样性正则化以外的方法已经广泛的应用在CNN和GAN中了,MHE可以看做是这些方法的补充。
3 最小化超球面能量神经元学习
3.1 最小超球面能量公式化
最小超球面能量定义了神经元方向的一个平衡的状态。我们认为,每一层的神经元的表达能力可以通过神经元的超球面能量来表示,最小的神经元能力意味着好的泛化能力。在深入细节之前,我们先定义一下N个d+1维神经元的超球面能量方程:
其中,f是递减的实函数,wi-hat是w的归一化之后的值,是第i个神经元在单位球面上的投影。f有很多的选择,在文中,我们使用,s>0,这叫做Riesz s-kernels 。特别的,当s->0,->,这个是的仿射变换,当我们最优化超球面能量的对数的时候,是符合最优化超球面能量的极限情况的。为了方便,我们定义 。
MHE判别式的目的是通过多样化神经元权重的方向来最小化式子(1)中的能量。实际上,我们求解这个最优化问题:,其中s≥0,特别的,当s=0的时候,我们求解对数能量最小化问题:
在这里,本质上是最大化了欧式距离的内积,E0,E1和E2是有深远的联系的,注意,Thomson问题优化的是E1,这是个NP-hard的问题,我们在实践中只能计算近似解,在神经网络中,这种可微分的目标函数是可以通过梯度下降来优化的。
3.2 使用对数超球面能量E0进行松弛
使用式1最优化原始的能量,等效于最优化它的对数,为了有效的求解这个最优化问题,我们可以最优化logEs的下界,作为能量的代理。使用Jensen不等式:
我们发现Elog变成了sE0,也就是对数超球面能量E0乘以s,因此,最优化E0也可以看做是对于s>0时,最优化Es的一个松弛版本。
3.3 将MHE作为神经网络的正则化
现在,我们介绍了MHE的公式,我们提出了神经网络的MHE正则化,在神经网络监督学习中,整个目标函数如下:
其中,x_i是第i个样本的特征,是分类层的第i个类别的权重,是经过归一化之后的权重,{Es}i表示第i层的神经元能量,c是类别数量,m是batch size,L是层的数量,l2的weight decay这里忽略掉了,但是实际中还是用的。另外一种MHE的正则化的解释来自于3.7节和附录C。在正则化隐藏层和输出层上,MHE具有不同的左右和解释。
MHE对于隐藏层 为了让隐藏层中的神经元变得更具可分性,冗余更少,我们使用MHE正则化,MHE让归一化之后的神经元均匀分布在一个单位球面上,在某种程度上,MHE最大化不同神经元之间的角度的平均值,例如,在CNN中,我们最小化卷积核和处输出层之外所有全连接层的超球面能力。
MHE对于输出层 对于输出层,我们提出通过使用MHE来学习可分性的特征,提高类内特征的可分度。对于分类任务,MHE正则化是softmax交叉熵的一个补充,softmax的损失更多的聚焦于类内的紧密性,而MHE趋向于内间的可分能力。因此,MHE用在输出层上可以使得特征具有更好的泛化能力。
3.4 半空间的MHE
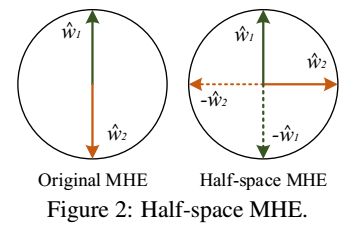
直接使用MHE仍然会遇到一些冗余的问题,例如,在图2中,在2维空间中有两个神经元,直接使用MHE的话,会导致这两个神经元共线,但是方向相反,为了避免这种冗余,我们提出了半空间的MHE正则化,构建一组虚拟神经元,然后对真实的神经元和虚拟的神经元一起进行最小能量的优化。特别的,半空间MHE为每个神经元构建一个相反方向的虚拟神经元。因此,最终我们需要在第i层上对2Ni个神经元进行最小能量的优化。这种半空间的多样性将驱动神经元具有更小的相关性和冗余性,如图2所示,半空间的MHE只是用在隐藏层中,因为在输出层中,共线性的神经元不会出现冗余的问题。共线性问题在高维空间中不太会发生,特别是当神经元对输入数据进行拟合的时候,这也许就是为什么原始的MHE仍然会提升baseline的原因。
3.5 MHE不仅仅是欧式距离
超球面能量原始定义是基于欧式距离的,可以看做是角度的度量。对于欧式距离,我们进一步考虑地理距离作为神经元之间的距离的度量,这个和角度的度量是完全一致的。特别是我们用arccos( wiwj)来代替||wi-wj||,顺着是个思路,我们提出了角度MHE,A-MHE,作为一个简单的扩展,其中超球面能量可以写成:
可以看做是基于地理距离,重新定义了MHE,可以用来替代(4)式中的Es,注意,A-MHE也可以在全空间或者半空间中学习,和原始的MHE具有同样的多样性,和MHE的关键区别在于优化时的状态,因为梯度的计算是完全不一样的,A-MHE的计算要比MHE更复杂。
3.6 MHE的mini batch近似
一个层中有非常多的神经元,计算MHE会计算量非常大,因为需要计算每一对神经元的距离,为了解决这个问题,我们提出了MHE的mini batch版本,用来近似MHE。
在隐藏层中使用mini batch近似MHE 对于隐藏层,迭代的使用一个随机的batch的神经元作为输入,最小化超球面能量,作为MHE的近似。注意,mini batch的目标的梯度是原始的MHE的无偏估计。
在输出层中使用数据依赖的mini batch近似MHE 对于输出层,迭代的取当前mini batch中存在类别对应的神经元,然后在每个迭代中最小化
其中,yi是第i个样本的类别标签,m是mini batch的大小,N是神经元的数量。
3.7 讨论
和科学问题的联系 超球面能量的最小化问题和科学问题的关系很密切。当s=1的时候,(1)式成为Thomson问题,需要在单位球体上让N个电子的分布具有最小的电势能。当s=∞的时候,式(1)变成Thomsom问题(地理上),把一组点放在单位球面上,让点之间的平均距离最小。当s=0时,式(1)变成whyte问题,目标是最大化欧式距离的内积,也就是式(2)。我们的目的是,利用这些重要的见解来提升神经网络的能力。
从解耦的观点来理解MHE 从解耦网络收到启发,我们可以把原始的卷积看成是角度函数和幅度函数的乘积:,其中,θ是卷积核w和输出x的角度,从上面的式子,我们可以发现,卷积核的长度和角度影响内积相似度的大小,特别的,权值衰减是对卷积核最小化L2的长度,没有对方向进行正则化。因此,MHE通过角度的多样性填补了这个部分,通过将MHE补充到标准的神经网络中,整个正则化项变为:
其中,λw,λh,λo是正则化项的超参数。从解耦的角度,MHE对于神经网络的正则化很有意义,因为它是权值衰减的一个补充。
和正交/角度提升正则化的对比 提升基之间的正交性或者角度是增加多样性的一个流行的方法。可能是最相关和广泛应用的正交正则化方法,目的是最小化,其中,W是神经元的权重,每一列是一个神经元,I是单位矩阵。有一个相似的正则化是正交性正则化,最小化所有的核参数的余弦值的和。而MHE是驱动这些核在单位球面上分布多样化,这些核不需要相互正交。还有的工作 提出了一个角度的限制,目的是限制不同kernel之间的角度,这和MHE也不同,他们使用了一个硬限制来进行角度的正则化。总的来说,这些方法的多样性正则化大都在一个局部的层次上,同时MHE寻找一个自顶向下的方法来建模这个问题。
MHE中的归一化的神经元 从式(1)中可以看到,计算MHE时需要用到归一化之后的神经元,因为我们的目的是在单位球面上进行多样化。这样,会有一个很自然的问题,我们如果使用原始的神经元会怎么样?首先,在MHE中带上长度会导致微小的梯度方向:简单的增大所有的kernel的长度。假设所有的kernel的方向是保持不变的,增加所有的kernel的长度会导致目标函数下降。第二,和长度耦合起来会导致和权值衰减矛盾。如果我们需要对不同的神经元赋予不同的重要性,我们也可以手工的给每个神经元一个固定的权重。这在我们已知一些神经元比其他的更加重要,而且我们需要固定这些权重的时候是很有用的。具有大的权重的神经元更新的会少一些。
4 理论的见解
5 应用和实验
5.1 提升网络泛化能力
首先,我们用MHE做一些探索性的实验,我们将MHE用在大规模物体识别和类别不均衡的学习上,所有的CIFAR10和CIFAR100上的实验,我们都使用了数据增强,对于ImageNet2012,我们也使用了同样的数据增强,我们使用SGD,动量为0.9,所有的网络使用BN和ReLU,实验细节在附录A。
5.1.1 MHE的探索性实验
MHE的变种 我们在CIFAR10和CIFAR100上实验了MHE的各种变化,包括原始的MHE,半空间带欧式距离和角度的MHE,所有的实验使用CNN-9,结果显示在Table1,可以看到,所有的变种都优于baseline,特别的,半空间的MHE提升的更多。MHE的欧式距离和角度距离的表现差不多,总的来说,s=2的结果要比s=0,1要好。在下面的实验中,我们默认使用s=2和欧式距离。
网络宽度 我们用不同的网络宽度来评估MHE,我们使用CNN-9作为基础网络,然后改变滤波器数量,结果在Table2中,可以看到MHE和半空间MHE仍然比baseline要好,还可以看到,在神经元少的时候,MHE能获得更大的提升,说明MHE对于神经元的利用性更好,通常来说,半空间MHE要比MHE好,这显示了减小共线性对于减少冗余的作用。
网络深度 我们使用不同的深度来评估MHE,我们固定滤波器的数量为64,128,256,我们对比了CNN-6,CNN-9,CNN-15,结果在Table3,MHE和half-space MHE都比baseline好,有趣的是,CNN-15不能收敛,但用了MHE后,又可以收敛了。half-space MHE仍然要比MHE好。
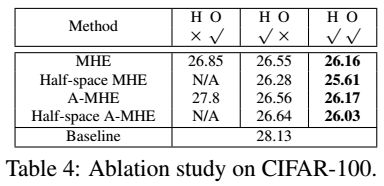
剥离研究 因为目前,MHE同时对隐藏层和输出层神经元做正则化,我们做了个剥离研究,看看提升是来自哪里。实验使用CNN-9,结果显示在Table4,“H"表示我们把MHE用在隐藏层中,”O"表示我们把MHE用在输出层中,由于半空间MHE不能用在输出层,所以,表中有“N/A"的值。我们发现,在隐藏层和输出层中同时使用MHE会得到最好的性能,在隐藏层中使用MHE要比在输出层中使用MHE效果要好。
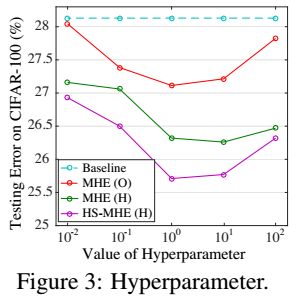
超参数实验 我们评估了超参数的选择会如何影响性能,我们使用了不同的超参数,从10e-2到10e2,使用了CIFAR100数据集,使用了CNN-9,使用了半空间的MHE。实验表现见图3,说明我们的方法对超参数不是非常的敏感,都比baseline要好。相比之下,权值衰减的超参数要比MHE的超参数敏感的多,半空间MHE还是要比MHE好,只在隐藏层中使用MHE要比只在输出层上使用MHE要好。
MHE对于ResNet 除了标准的CNN,我们还在ResNet-32上进行了评估,看看我们的MHE是不是可以在不同的结构上都可以取得提升。除了ResNet-32,还评估了GoogleNet,SphereNets,DenseNet等。具体的结构在附录A中,结果见Table5。可以看到,用在ResNet-32上,同样可以获得不少的提升,说明MHE可以适用于不同的网络结构。更加重要的是,使用MHE不会影响原有的结构,可以通过一个非常小的代价获得性能的提升。
5.1.2 大规模物体识别
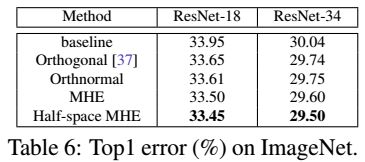
我们在ImageNet-2012数据集上评估了MHE,我们使用了ResNet,Top1的验证误差见Table6,可以看到,MHE和半空间MHE依然比baseline和正交正则化要好,为了更好的验证MHE的提升,我们使用了两个不同深度的网络,ResNet-18和ResNet-34,两个网络上,MHE和半空间MHE都比baseline要好,其中半空间MHE要比MHE要好。
5.1.3 类别不均衡的学习
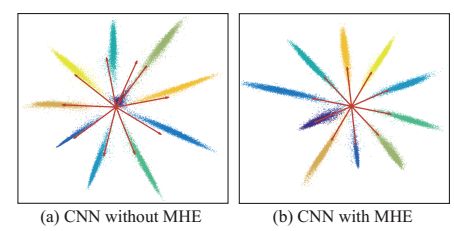
由于MHE的目的是最大化不同类别在超球面上的margin,我们可以很自然的将它用到不均衡类别的分类中,我们通过一个toy数据集来验证MHE的能力,我们随机的把98%的minist数据集中的数字0的样本扔掉,然后训练了一个不均衡的mnist,为了可视化特征,我们把输出维度降为2,可视化图将图4。每个颜色代表了一个数字,红色的箭头代表了归一化的分类神经元。虽然我们是在不均衡的数据集上训练的,我们在所有的训练数据上进行更好的可视化。可以看到,没有使用MHE的时候,分类器趋向于忽略数字0,相比之下,使用MHE的分类器对于数字0的预测分布和其他的数字一样。使用了MHE在这个toy数据集上,可以将测试准确率从88.5%提升到98%。更加重要的是,数字0的神经元也学习的很好,就和在均衡数据集中一样。注意一下,半空间的MHE不能用在分类神经元中,因为分类神经元往往需要占据整个空间。
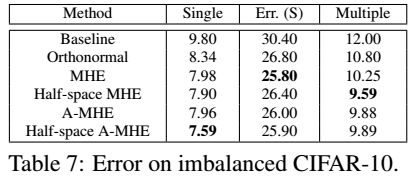
我们在CIFAR10上使用了两种不均衡数据集的设置:(1)单个类别不均衡(S),也就是所有的类别具有相同的图像数量,只有一个类别图像数量非常少。(2)多类别不均衡(M),图像的数量随着类别标签从9到0递减。我们使用CNN-9来做所有的实验,细节设置在附录A,结果在Table7,我们可以看到,MHE可以显著的提升类别不均衡数据集的表现。在附录H中,我们还提供了CIFAR100的实验结果。
5.2 SphereFace+:通过MHE为人脸识别增加类间特征可分性
我们展示了全空间的MHE可以分类神经元的分布在超球面上更加均匀,从而提升特征的可分析。直觉上,分类神经元就代表了每个类别的中心特征向量,可以知道特征的学习。我们还发现,对于Open-set的人脸识别,需要学到的特征具有最大的可分性。这个联系,使得我们可以将MHE应用到人脸识别中。特别的,我们将MHE应用到SphereFace中,提出了SphereFace+,SphereFace的目标,使用角度的softmax来增加特征的内聚性,和MHE天然互补。SphereFace+的目标函数可以定义为:
其中,c是类别的数量,m是mini batch的大小,N是分类神经元的数量,是第i个人脸的特征,是第i个分类神经元,是SphereFace的超参数,控制内聚的程度。由于人脸识别数据集往往有几千个类别,我们使用数据依赖的近似MHE,如式(8),在输出层中使用,减少计算量。 MHE填补了SphereFace的缺失部分,就是特征的可分性。SphereFace+明显优于SphereFace,在LFW,MegaFace数据集上取得了state of the art。MegaFace的结果在附录I,更多的SphereFace+的评估见附录F和J。
不同下的表现 我们在两个不同的结构上评估了SphereFace+,SphereFace-20和SphereFace-64,这两个都是基于ResNet的网络结构,我们使用公开的CASIA-WebFace数据集来训练,在LFW和MegaFace数据集上测试,在MegaFace数据集上,我们在1百万的干扰项下报告了rank1的识别准确率。结果见Table8,Table9,结果没有经过集成或者PCA,可以发现,SphereFace+明显优于SphereFace,包括使用不同的设置。
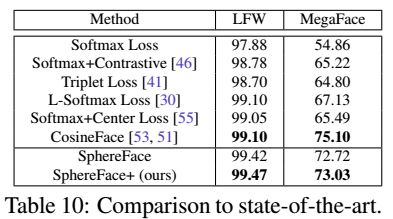
和state of the art的方法对比 我们也和一些广泛使用的损失函数进行了对比,所有的方法都是用了SphereFace-64的网络,在CASIA-WebFace数据集上训练,结果在Table10中,没有集成和PCA。对比不同的方法,SphereFace+在LFW上取得了最好的结果,在MegaFace上也取得了相当好的成绩。当前的人脸识别方法往往聚焦于特征的内聚性,这使得MHE是一个很有潜力的工具,可以提升人脸识别的能力。
6 总结
我们从物理中借用了一些思想,为神经网络提出了一个新的正则化的方法,叫做最小超球面能量(MHE),用来增加神经元角度的多样性。MHE可以非常方便的插入到每一层中,作为正则化,而不用改变原来的结构。和现有的方法不同,MHE特别用在了图像分类,不均衡数据集,人脸识别的任务中,增加网络的泛化能力。更进一步,你还可以用MHE来增加GANs生成图像的质量(附录G)。总的来说,我们通过超球面的多样性提出了一种新的正则化方法。